帶負顧客和啟動時間Bernoulli反饋M/M/1工作休假排隊

朱少平，王 珍

帶負顧客和啟動時間Bernoulli反饋M/M/1工作休假排隊

*朱少平，王 珍

(井岡山大學數理學院，江西，吉安 343009)

在Bernoulli反饋的情形下考慮帶有負顧客和啟動時間的M/M/1工作休假排隊模型，畫出了狀態轉移圖，給出了無窮小生成元，利用擬生滅過程與矩陣幾何解方法，得到了穩態隊長和穩態等待時間的分布。另外，還得到了隊長和等待時間的條件隨機分解結構及附加隊長和附加延遲的分布。

負顧客；Bernoulli 反饋；啟動時間；工作休假；隨機分解

工作休假是一種半休假策略，由文獻[1]首次提出，相關的研究還有文獻[2-3]。文獻[4]綜合研究了排對論中的負顧客，帶有反饋的排隊系統在生產和實際生活中都有很重要的意義，帶反饋的排隊系統與經典排隊系統的服務機制相比所有變化，顧客到達系統后并不一定經過一次服務就離開系統，可能經過多次，這個服務次數是由反饋機制所決定的。帶反饋的服務系統的研究為實際工作中遇到的具體模型提供了一種有利的數學工具，文獻[5-6]中有相關的模型研究，其中Bernoulli反饋已被廣泛應用于計算機分時操作系統和無線電通訊網絡系統中，通過對其某些指標的研究，可安排最合理的方案。

1 模型的描述

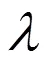
（4）服務員對正顧客在正規忙期和工作休假期的服務時間分別服從參數為1和2的負指數分布，其中2＜1；

（5）當一次工作休假結束時，如果系統中有正顧客，服務臺立即轉入正規忙期對顧客進行服務，服務率由2變為1，一個正規忙期開始，此時正在接受服務的正顧客重新開始接受服務；……