在NA樣本下一類雙邊截斷型分布族參數(shù)的經(jīng)驗Bayes估計

劉榮玄

在NA樣本下一類雙邊截斷型分布族參數(shù)的經(jīng)驗Bayes估計

劉榮玄

（井岡山大學(xué)數(shù)理學(xué)院，江西，吉安 343009 ）

在平方損失下，討論一類雙邊截斷型均勻分布族參數(shù)的經(jīng)驗貝葉斯（EB）估計的漸近性。按照貝葉斯（Bayes）方法，導(dǎo)出均勻分布族參數(shù)的Bayes估計，利用歷史樣本，采用概率密度函數(shù)的核估計方法，構(gòu)造出邊緣密度函數(shù)的估計，從而得到參數(shù)的EB估計，在一定的條件下，證明所得到的EB估計是漸近最優(yōu)的，而且得到了其收斂速度，最后舉例說明滿足定理條件的參數(shù)的先驗分布是存在的。

NA樣本；均勻分布；平方損失；Bayes估計；漸近性

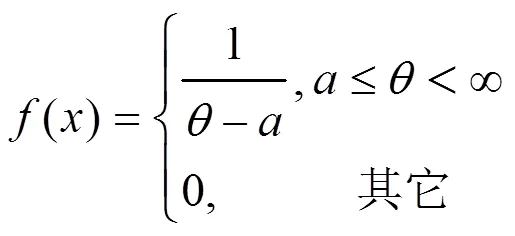
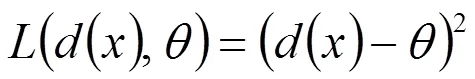
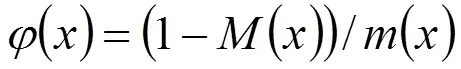
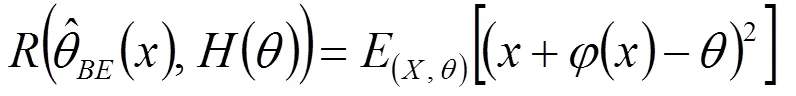
1 EB估計的構(gòu)造

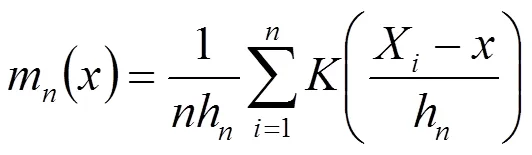
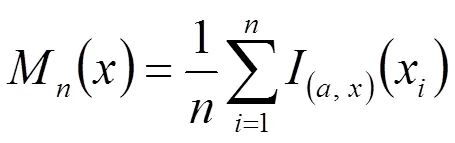
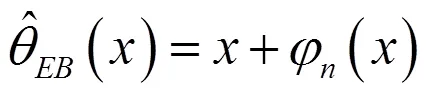
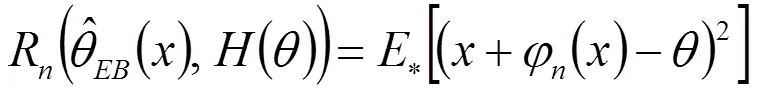
2 EB估計的漸近性

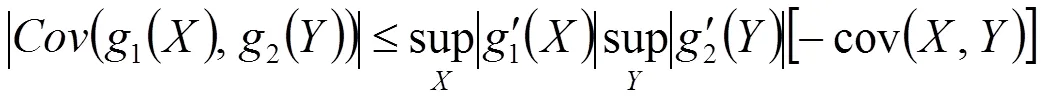
證明 見文獻(xiàn)[5]引理1。

引理2 在均方損失下，有

證明 見文獻(xiàn)[6]的引理2.1。

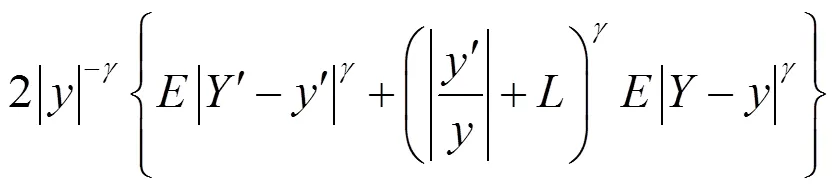
證明 見文獻(xiàn) [7]引理3.1。

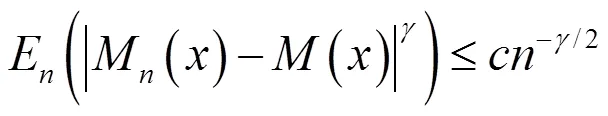
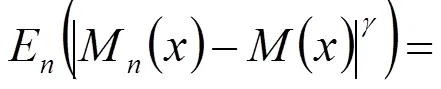
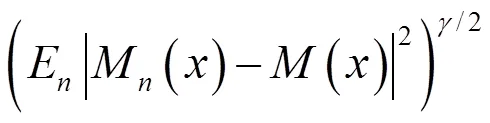
綜合可知引理結(jié)論成立。

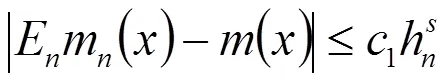
， (2.7)

由引理1可得

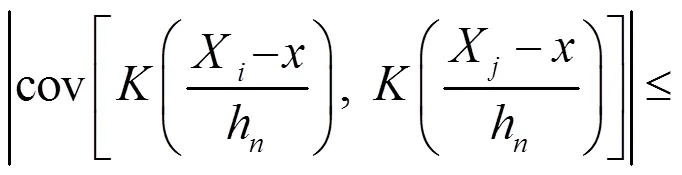
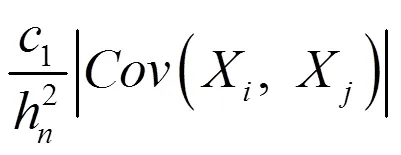
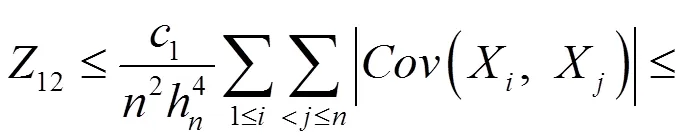
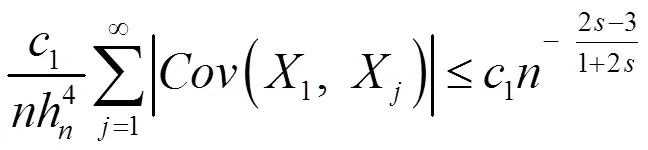
于是有

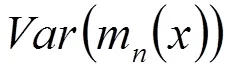
由C-R不等式和Jensen不等式以及（2.6）、（2.10）式得

則有

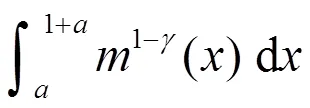
， (2.12)

綜合式(2.12)和(2.13)可知，(2.11)成立。

又由凸函數(shù)的Jensen不等式有

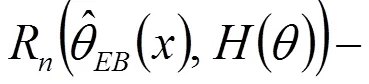
證明 由引理2有

其中

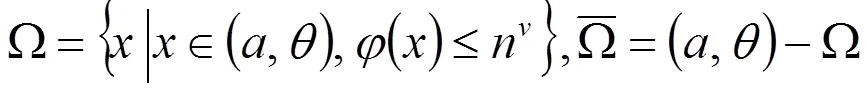
由引理3、引理4和引理5有

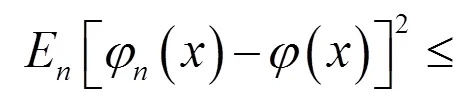
由引理6得到

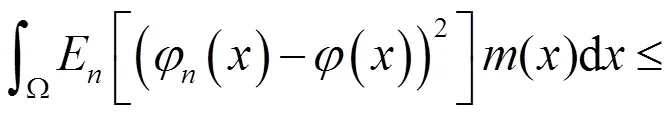
(2.16)

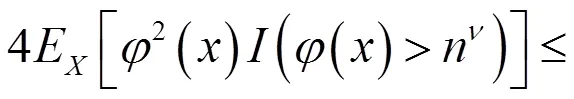
(2.17)

3 例子

下面的例子說明存在滿足定理條件的先驗分布。

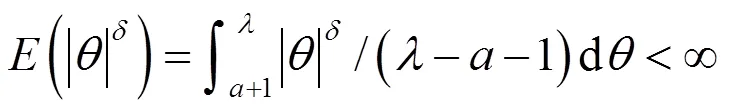
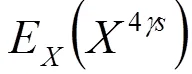
到此可知定理中的條件全都成立，則定理的結(jié)論成立。

[1] 韋來生.刻度指數(shù)族參數(shù)的經(jīng)驗貝葉斯檢驗問題:NA樣本情形[J]. 應(yīng)用數(shù)學(xué)學(xué)報,2002(3):198-201.

[2] 許勇,師義民.NA樣本情形下單邊截斷型分布族位置參數(shù)的經(jīng)驗Bayes估計[J]. 應(yīng)用數(shù)學(xué),2001,14（4）：98-102.

[3] 康會光,趙小山.Linex損失函數(shù)下單邊截斷型分布族參數(shù)的EB估計[J]. 應(yīng)用數(shù)學(xué)，2001,14（3）：82-86.

[4] 劉榮玄,曹艷華.雙指數(shù)分布族參數(shù)EB估計的最優(yōu)性[J].華中師范大學(xué)學(xué)報:自然科學(xué)版,2011,45(4):542-546.

[5] Wei L S.Convergence rates of empirical Bayes estimation for arameter ofone-sided truncated distribution[J].Annals of Math,1985,6A(2):193-202.

[6] Singh R S.Empirical Bayes estimation in Lebesgue- exponential families With rates near the best possible bate[J].Ann Statist,1979,7(4):890-902.

[7] 趙林城.一類離散分布參數(shù)的經(jīng)驗貝葉……