兩類映射的近似耦合不動點定理

賈必偉，仇秋生

兩類映射的近似耦合不動點定理

*賈必偉，仇秋生

(浙江師范大學數學系，浙江，金華 321004)

在度量空間中，討論了近似耦合不動點存在性問題。首先研究了廣義非擴張型映象的近似耦合不動點。作為應用，獲得了賦范空間中有界集上的非擴張映象的近似耦合不動點。其次在半序度量空間中討論了非連續混合單調算子的近似耦合不動點存在定理。

近似耦合不動點；非擴張映象；混合單調算子

非擴張映象是Banach壓縮映象的一種自然的推廣，這種映象在近代許多數學分支，其中特別是在非線性半群，遍歷理論和單調算子理論有許多重要的應用。關于非擴張映象不動點理論Marr[1]得出著名的Kaku tani-Markov不動點定理的一些推廣；Lim[2]證明了在一致凸Banach空間集值非擴張映象不動點的存在性；Kirk和Massa[3]將Lim’s的結果推廣到Banach空間，其中要求Banach空間的有界閉凸子集的一個有界序列的漸進中心是非空緊的；Lan和Zhang[4]研究了定義在Banach空間(或廣義局部凸空間) 弱緊凸子集上的半群非擴張映象的不動點性質。眾所周知，單調迭代技術在處理許多非線性問題時起著至關重要的作用。這類技術與混合單調算子不動點有密切的聯系。半序Banach空間中單值混合單調算子不動點定理已有廣泛研究[5-7]；最近，集值混合單調算子不動點定理被許多作者關注[8-9]；其中文獻[8]，在半序Banach空間討論了集值混合單調算子的耦合不動點的存在和逼近問題，其中算子要求滿足稠密條件且上半連續；Laksh和Ciric[10]在完備半序度量空間證明了連續混合單調非線性壓縮映象的耦合不動點定理；而后Karapinar[11]將其推廣到完備錐度量空間，其中錐為正則錐。

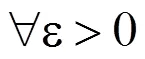
1 預備知識

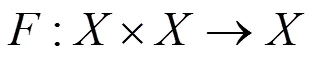
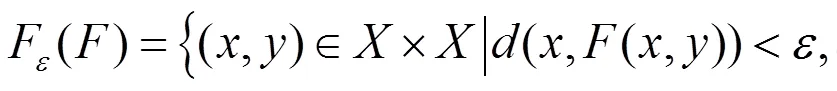
則稱具有近似耦合不動點性質。

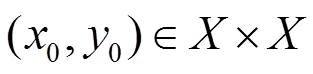
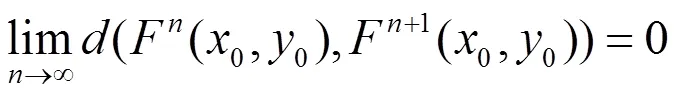
則具有近似耦合不動點性質。

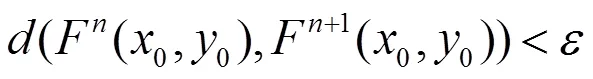
即

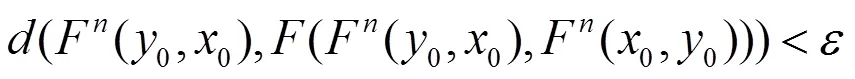
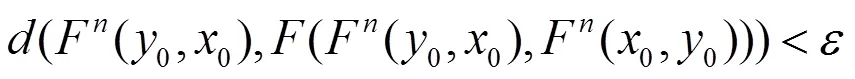
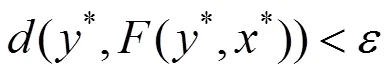
2 非擴張映射的近似耦合不動點定理

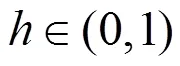
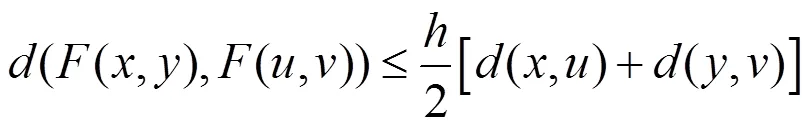
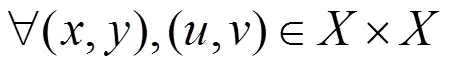
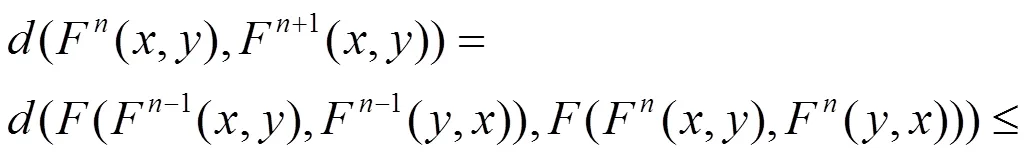
一般的，有

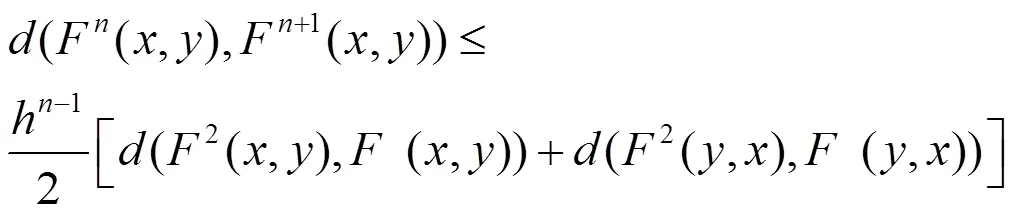
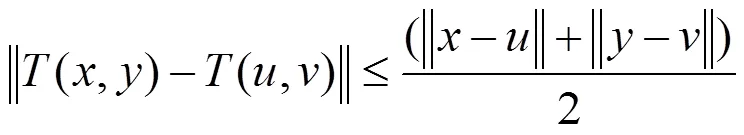
則具有近似耦合不動點性質。

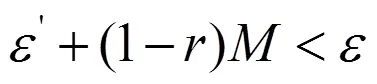
由 (2) ，有

于是滿足條件(1)。

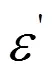
使得

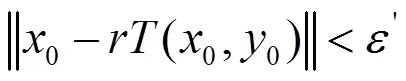
則

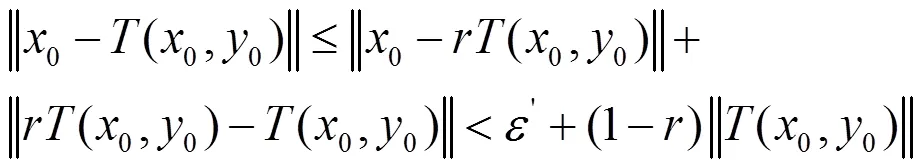
同理有

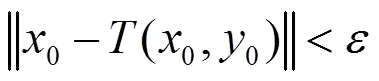
則具有近似耦合不動點性質。

注2.1：非擴張映象不一定有不動點，但當為有界集時，非擴張映象

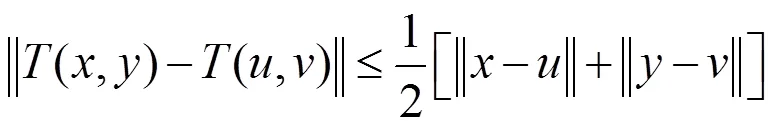
有近似耦合不動點。

下面定理及推論證明了Kannan型非擴張映象在為有界集的情況下，存在近似耦合不動點。

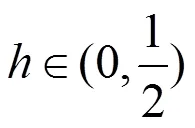
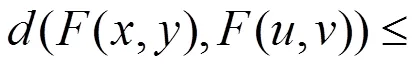
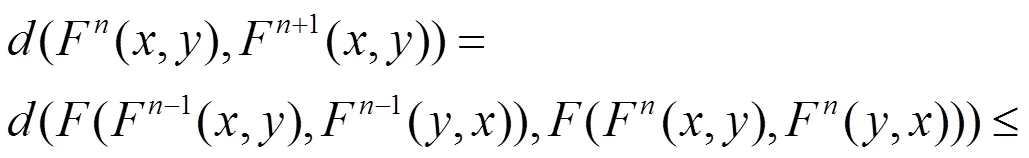
則

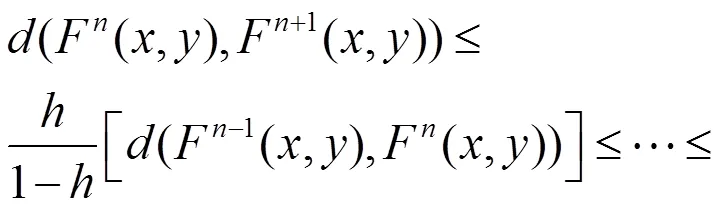
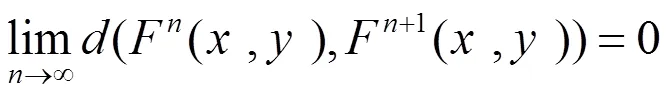
類似于定理2.2 的證明，由定理2.3 可得下列推論。

,

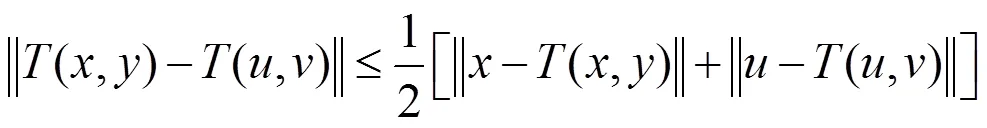
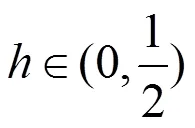
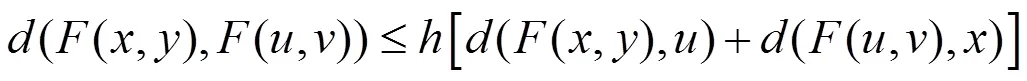
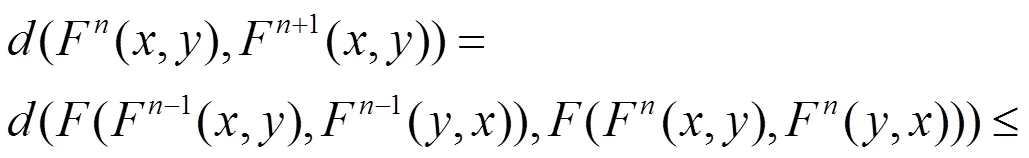
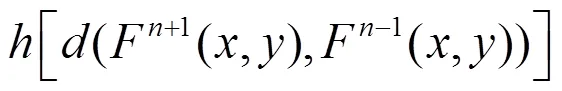
又

所有患者每6個月進行1次電話隨訪，末次隨訪日期為2018-02-28。隨訪時間 5～50個月，中位隨訪時間32.1個月,期間有36例患者復發，13例患者死亡。復發轉移要求有病理診斷或者典型的影像學及臨床表現，復發和生存時間按月記錄，以手術日至患者復發、死亡或最后一次就診(隨訪)時間為復發或生存期限。失訪，非腫瘤死亡及截止點生存病例按統計分析要求列為截尾數據處理。

故

。 類似定理2.3 證明，有 由引理1.1 得，，。 推論2.2 設E為一賦范空間，為有界集，映射滿足非擴張條件： ， 則具有近似耦合不動點性質。 3 混合單調算子的近似耦合不動點 定義3.1[11] 設為一個半序集，映射，，稱具有混合單調性質，若， 。 定義3.2 (X,d)為度量空間，映射 ， ， ，若 稱F關于g具有近似耦合不動點性質。 定義3.3 [11] ，映射，，稱映射F與g為互換的，如果 BY-4型納米陶瓷基高溫防氧化涂層材料對鋁電解用碳素陽極的抗氧化應用 李順華，王博一，楊國榮，等 4 73 表現器樂本身就是一種對美的探索與表現的過程。學習樂器技能時，教師應不拘一格、靈活多樣的指導學生學習，避免單調乏味的純技術訓練，通過多樣教學將器樂技巧融于課堂教學中，提升教學實效。 , 。 定理3.1 (1)設，為一個半序集，(X,d)為度量空間；(2) ，滿足，且；(3)F:X×X→X，，F具有混合g-單調性質，滿足下列條件： (i)對所有滿足，的，有 ； (ii)，F與g互換； (iii) 存在，使 ， ，則 ， 。 證明 由條件 (iii) ，存在，使，。 又由于，構造序列，滿足，。 下證序列，為單調序列。利用數學歸納法，當時，由， 及 ， 得 ， 。 假設， 成立，由F具有混合單調性質有 2018年三季度，在二、四季度“618”、國慶、雙十一等促銷節點的前后擠壓下，部分消費需求被分流，疊加宏觀經濟環境變化和房地產市場調控的影響，家電市場整體表現不盡人意。然而分品類來看，依然有一些亮點呈現，比如生活電器的高速增長，冰洗市場的結構升級成效正在凸顯。 故對所有 ， ， 成立。令 由于 則 同理。 11月16日凌晨，巴陵石化煤化工部儀表車間合成班值班員蔣正流接到合成車間工藝四班人員報告后，立即趕往合成總控制室。“我們詢問了各運行部，都沒有同類型的冗余通訊卡備件。詢問備件廠家，他們答復從北京郵寄，最快也要兩天。”儀表車間主任姜文偉說。 從而有。 又當時，，則 則為單調遞減序列，那么存在，有。 有關傳承人的界定，各國的確定標準和程序大有不同，非物質文化遺產法就對我國代表性傳承人的認定標準作出了清晰的規范和界定。目前的認定標準是：首先繼承者應當精通并能駕馭其繼承的屬于非物質文化遺產的技藝技能；其次他們還應當在某些特別的地域中擁有較大的知名度和感染力并且具有象征性；最后還應當踴躍地發展和傳播與承繼相關的活動和事業。而關于認定程序，要嚴格根據相關法律法規對國家級象征性項目的規定認真審批，并向社會公布通過認定的具有代表性的傳承人的名單。 假設，考慮到，，則由 兩邊取極限 有 結合描述性統計分析，532家樣本企業中成功獲取銀行貸款的為480家，貸款利率平均上浮71.4%，抵押貸款筆數占比為68.1%。樣本企業中22.1%的小微企業選擇向五大商業銀行申請貸款，77.9%的企業選擇向股份制商業銀行、城市商業銀行等申請貸款。從負債率來看，小微企業的整體負債水平較低，均值為38.65%，平均年銷售收入為3 280萬元。關系深度(rela_de)均值為0.751，表明大多數小微企業傾向于選擇其主要關系銀行作為貸款申請對象；平均關系年限僅為2.79年，這與大多數小微企業為初創型、成立年限較短有關。 矛盾。 從而有，即 則，，，有。 即 ， 。 同理 ， 。 令， 則有 同理。 從而，。 注3.1：令 ，，得到推論3.1。 推論3.1 設，為一個半序集，(X,d)為度量空間，映射，，F具有混合g-單調性質，滿足： (i)對所有滿足，的，存在，使 ； (ii) ，F與g互換； (iii) 存在，使 ， ，則 ， 。 注3.2：當，立即得到下述推論。 推論3.2 設為一個半序集，(X,d)為度量空間，映射為混合單調算子，滿足： (i) 對所有滿足, 的，存在，使 ； (ii) 存在，使， ，則 ， 。 參考文獻： [1] DeMarr R. Common fixed points for commuting contractions[J]. Pacific J. Math, 1963, 13: 1139-1141. [2] Lim T C. A fixed point theorem for multivalued non-expansive mappings in a uniformly convex Banach space[J]. Bull. Amer. Math. Soc, 1974, 80: 1123-1126. [3] Kirk W A, Massa S. Remarks on asymptotic and Chebyshev centers[J]. HoustonJ. Math, 1990, 16(3): 357-364. [4] Liu A T, Zhang M Y. Fixed point properties of semi-groups of non-expansive mappings[J].Journal of Functional Analysis, 2008, 254: 2534-2554. [5] Wu Y S, Li G Z. On the fixed point existence and uniqueness theorems of mixed monotone operators and their applications[J]. Acta. Math. Sci, 2003, 46: 161-166 (in Chinese). [6] Zhang Z T. New fixed point theorems of mixed monotone operators and applications[J]. J. Math. Anal. Appl, 1996, 204: 307-319. [7] Gun D, Lakshmikantham V. Coupled fixed points of nonlinear monotone operators with applications[J]. Nonlinear. Anal, 1987, 11: 623-632. [8] Huy N B, Khanh N H. Fixed point for multivalued increasing operators[J]. J. Math. Anal. Appl, 2000, 250: 368-371. [9] Hong S H. Fixed points of discontinuous multivalued increasing operators in Banach spaces with applications[J]. J. Math. Anal. Appl, 2003, 282: 151-162. [10] Laksh V, Ciric L. Couple fixed point theorems for nonlinear contractions in partially ordered metric spaces[J]. Nonlinear. Anal, 2009, 70: 4341-4349. [11] Karapinar E. Couple fixed point theorems for nonlinear contractions in cone metric spaces[J]. Comp. Math. Appl, 2010, 59: 3656-3668. [12] Cromme L J, Diener I. Fixed point theorems for discontinuous mapping[J]. Math. Programming(ser.A) 1991, 51(2):257-267. [13] Hou S H, Ya C G. Approximate fixed points for discontinuous set-valued mappings[J]. Math. Meth. Oper, Res,1998, 48: 201-206 . [14] Tijs S, Torre A, R Branzei. Approximate fixed point theorems[J]. Libertas Math,2003, 23:35-39. [15] Branzei R, J Morgan, V Scalzo, et al. Approximate fixed point theorems in Banach spaces with application in game theory[J]. J. Math. Anal. Appl, 2003, 285:619-628. [16] Berinde M. Approximate fixed point theorems[J]. Stud. Univ. “Babes, Bolyai”, Math, 2006, 51(1):11-25. [17] Prasad B, Singh B, Sahni R. Some approximate fixed point theorems[J]. Int. Journal of Math. Analysis, 2009, 3(5):203-210. [18] 張石生. 不動點理論及應用[M].重慶：重慶出版社,1984. APPROXIMATE COUPLE FIXED POINT THEOREMS FOR TWO KINDS OF MAPPINGS *JIA Bi-wei, QIU Qiu-sheng (Department of Mathematics，Zhejiang Normal University，Jinhua，Zhejiang 321004, China) Abstract: In this paper, the existence problems of approximate couple fixed point are discussed on metric spaces. Firstly, the approximate couple fixed points of generalized non-expansive mappings are studied. As application, the approximate couple fixed points of non-expansive mappings in the bounded sets of normed spaces are obtained. Secondly, the existence theorems of the discontinuous mixed monotone operators in the partially ordered metric spaces are discussed. Key words: approximate couple fixed point; non-expansive mapping; mixed monotone operator 中圖分類號：O177.91 文獻標識碼：A DOI:10.3969/j.issn.1674-8085.2012.06.002 文章編號：1674-8085(2012)06-0006-06 收稿日期：2012-06-23； 修改日期：2012-09-18 基金項目：浙江省自然科學基金項目(Ly12A01005) 作者簡介：*賈必偉(1987-)，女，江蘇淮安人，碩士生，主要從事最優化理論研究(E-mail: xiaxuejiabiwei@163.com); 仇秋生(1962-)，男，江西上高人，教授，博士，主要從事非線性泛函分析與向量優化理論研究(E-mail: qsqiu@zjnu.cn).