淺談積分概念的本質及內在聯系

徐志科

（中原工學院 廣播影視學院，河南 鄭州 450000）

淺談積分概念的本質及內在聯系

徐志科

（中原工學院 廣播影視學院，河南 鄭州 450000）

首先，分析積分概念的本質是某種和式的極限；其次，把這個本質運用在各類積分中，并探討了各類積分的關系及積分的計算；最后，談談積分的應用.

積分；極限；原函數

要深入透徹地理解學過的知識，在學習的時候，就要善于歸納小結.什么叫“深入透徹”？簡單說來，就是要領會概念、理論的本質，并了解知識的內在聯系.要做到這點必須多多思索.我們就積分學來談談這個問題.

在《微積分》課程的學習中，積分的學習是學生覺得比較困難的，首先，積分運算是微分運算的逆運算，逆運算難于正運算，計算難；其次，積分概念結構復雜，概念抽象，理解難；最后，積分方法應用廣泛，是解決實際問題的有力工具，運用難.不過作者認為只要抓住積分概念的本質及內在聯系，就可以實現以點帶面的學習.

1 抓住各類積分概念共同的本質屬性

在《微積分》中，我們分別學習過一元函數定積分、二重積分、三重積分、曲線積分和曲面積分（這里先撇開不定積分不談），各類積分來源于不同的現實模型.究竟積分概念的本質怎樣？各種積分有什么內在聯系？我們撇開其具體內容表象，抓住它們在數量關系上共同的本質與特性加以概括，就可以抽象出各類積分概念共同的本質屬性.

設在某一“區域”G定義了點函數f(P)（這里“區域”廣義地理解，后面將加以說明），我們定義f(P)在G上的積分：

（1）將G任意分割為n個子域σk，大小為△σk(k=1,2,…,n)；

（2）在每一子域σk中任意取點Pk；

如果不論G怎樣分割、Pk怎樣取法，這和數當最大子域的直徑δ趨于零時存在極限，這極限就稱為f(P)在G上的積分.

這樣看來，積分概念的本質是某種微元和式的極限，而構成定義的要素是：任意分割、任意取點、求和、取極限.

為什么有各種類型積分？“區域”G的選擇正是產生各種類型積分的原因.在一維數軸上，取“區域”G為區間[a,b]，被積函數為一元函數f(x)，上述積分即為定積分；在二維平面上，“區域”G可以取一般平面區域，也可以取平面曲線，被積函數為二元函數f(x,y)，就相應地有二重積分、平面線積分；在三維空間，情形就更復雜些，G可以取空間立體、空間曲線或空間曲面，就相應地有三重積分、空間線積分或面積分.

2 抓住各類積分計算的內在聯系

抓住了各類積分及不定積分與定積分關系，就可以從本質上解決積分的計算問題.

2.1 各類積分之間關系的論證

牛頓-萊布尼茨公式、格林公式、斯托克斯公式、高斯公式在本質上所反映的是不同維空間同一個數學關系，即它們都是將某一積分域上的積分用該積分域的“邊界”的另一類積分表示出來.一維空間的牛頓-萊布尼茨公式縱向發展成二維空間的格林公式，它把二重積分和線積分聯系起來，格林公式橫向推廣為斯托克斯公式，斯托克斯公式把線積分和面積分聯系起來，斯托克斯公式縱向發展成三維空間的高斯公式，高斯公式又把三重積分和面積分聯系起來，而二重積分、三重積分最終都化為定積分的計算，所以不管哪一類積分的計算，最后都歸結為一維空間定積分的計算.

各種積分計算上的聯系怎樣？就二重積分說，我們總化為累次積分來計算：

從上式看，如果掌握了定限技巧，二重積分就化為定積分問題；三重積分也一樣；線積分可以直接化為定積分；而面積分是先化為二重積分，再化為定積分，這樣，關鍵就在于計算定積分.

2.2 不定積分與定積分關系的論證

積分存在定理告訴我們，當被積函數在G上連續時，積分一定存在，正因為積分存在，實際計算上我們可以不必任意分割、任意取點，而可以特殊分割、特殊取點.例如，用定義計算定積分時，可以采取等分與取端點的方法.但這種計算方法在實際操作中是非常難，不可行的.

不定積分概念是某函數在區間I上所有原函數的集合，而定積分概念是一種“微元和式的極限”值，本來是兩個完全互不相關概念,但牛頓-萊布尼茨公式建立了不定積分與定積分之間的聯系，用原函數統一了積分與微分的關系，徹底解決了定積分的計算.

設F(x)是f(x)的一個原函數，由牛頓-萊布尼茲公式：

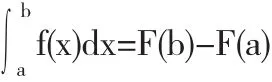
定積分又歸結為不定積分.這樣，各種積分的計算都歸結為不定積分的計算.同學們，這樣看來，不定積分是何等重要，必須努力掌握不定積分的基本運算，并且注意不要過多依賴積分表.應該指出，不定積分還有其他廣泛的應用.

我們再就牛頓-萊布尼茲公式，談談怎樣深入地理解理論.我們知道，原函數與定積分的概念是作為導數與微分的逆運算提出來的，正是牛頓-萊布尼茲公式建立了定積分與不定積分的深刻的本質聯系.因為F'(x)=f(x)，因而公式可以改寫為

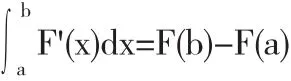
這一公式把導數與積分聯系起來，指明微分與積分是互為逆運算的關系.導數與積分是微積分學二個最基本的概念，求導與求積是二種最基本的極限過程，這就使得牛頓-萊布尼茲公式成為整個微積分學的樞紐.應該知道，不定積分是作為導數的逆運算的概念而引入，這與牛頓-萊布尼茲公式揭示的導數與積分互為逆運算的關系，是根本不同的.同學們必須把定義與定理、概念與理論區別清楚.

上面談的是定積分與不定積分的內在聯系.在理論上，其他各種積分也有深刻的內在聯系.例如，格林公式體現了平面線積分與二重積分的內在聯系.

3 理解積分的應用

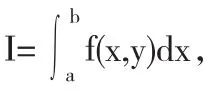
〔1〕許娟娟.微積分教學中學生思維品質的培養[J].赤峰學院學報(自然科學版),2011（12）：27-29.

〔2〕蕭樹鐵.大學數學 微積分(一)[M].北京：高等教育出版社,2003.

〔3〕劉玉璉.數學分析講義（上冊）[M].北京：高等教育出版社，2003.

〔4〕謝芳.《微積分》課程中積分的學習[J].高校理科研究,2010（12）：68.

O172

A

1673-260X（2012）06-0008-02