纏繞于一般曲面體上張緊力的有限元計算
吳 飛,李德華,莫玉林
(1.貴州大學 機械工程學院,貴州 貴陽,550003;2.中鋁長城建設有限公司 越南項目部,河南 鄭州,450041;3.西安理工大學 機械與精密儀器工程學院,陜西 西安,710048)
1765年,瑞士數學家歐拉對張緊纏繞于圓柱體上線繩的張力與纏繞角,推導了數學力學關系式,即歐拉公式,從而奠定了撓性體摩擦理論的基礎。在機械工業中,帶傳動、制動器、對物體的牽引、提升、搬運等都會涉及到柔性體的摩擦理論。經典歐拉公式對小角度纏繞于圓弧面上的線繩張緊力的計算很方便,若用經典歐拉公式計算接觸面為非圓弧面情況下的張緊力,誤差就很會大,對我們的工程應用會產生一定的影響。
本文介紹一種纏繞于一般曲面體上的廣義歐拉公式,運用ANSYA WORKBENCH對其進行有限元分析計算,對分析的結果和公式進行比較,最后得出結論。
1 纏繞于一般曲面體上的廣義歐拉公式
設一根線繩纏繞于一般曲面體上,接觸線為一般曲線。假設線繩是理想的撓性體,在工作中不能伸長,也無彎曲阻力存在,忽略線繩轉動時離心力的影響(v<10m/s)。如圖1所示,取一段接觸帶AB進行分析,并在AB弧上取一微小段線繩,其所對應的微小圓心角為,在該微弧段處的曲率半徑為R(s)。
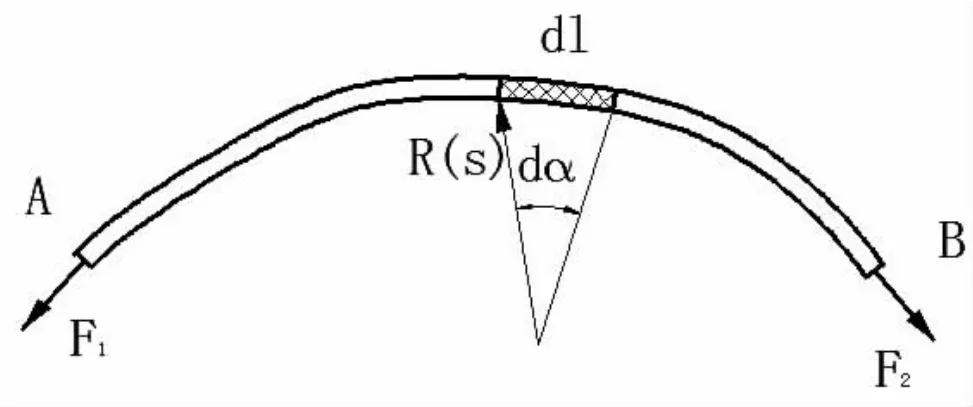
圖1 線繩纏繞于一般曲面體
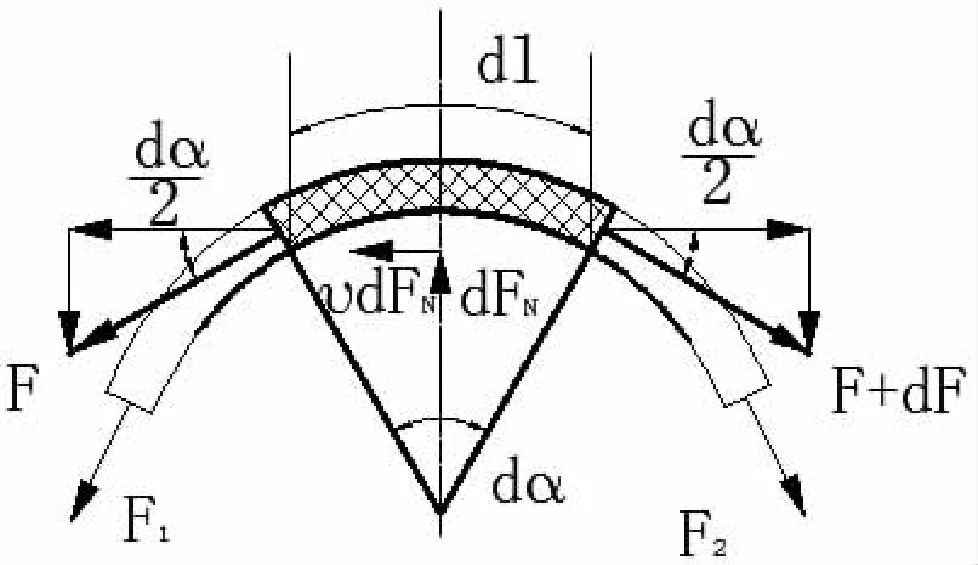
圖2 微段線繩的力平衡關系
如圖2所示,對微弧段dl作受力分析,其兩端受力分別為F和F+dF,線繩對轉筒的正壓力為dFN,其摩擦力為μdFN,μ為線繩與轉筒間的摩擦系數。線繩在即將打滑的臨界狀態下,各個力在水平和豎直方向的平衡關系為:
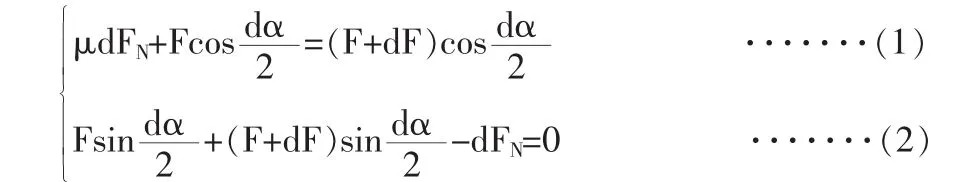
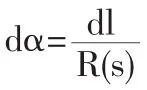
此即為纏繞于一般曲面體上的歐拉公式。
2 有限元計算
本文通過對一具體實例作有限元計算,分析卷筒纏繞時的線繩張緊力的情況,與用上述介紹的廣義歐拉公式分析的結果進行比較。以下采用solidworks建立三維模型,然后導入ANSYS WORKBENCH進行有限元分析計算。
2.1 建模
在solidworks中建立一纏繞于一般曲面體上的卷筒纏繞三維模型,該卷筒分別由6個圓弧面和平面交替組成。首先創建一個內接圓半徑為200mm的六邊形,再將其6個角用半徑為100mm的圓弧進行圓角,然后通過實體拉伸生成模型。該卷筒內徑為280mm,卷筒厚250mm,繞繩厚為30mm,寬為100mm,卷筒與繞繩間的摩擦系數為0.3,建立纏繞包角分別為 60°、120°、180°、240°、300°、360°的三維模型。如圖 3 所示纏繞包角為360°時的裝配體模型。在solidworks中將所建立的裝配體另存為Parasolid格式,再分別導入到ANSYS WORKBENCH中進行有限元分析。
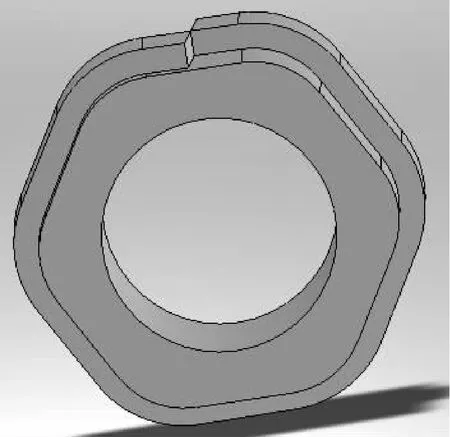
圖3 卷筒纏繞有限元模型
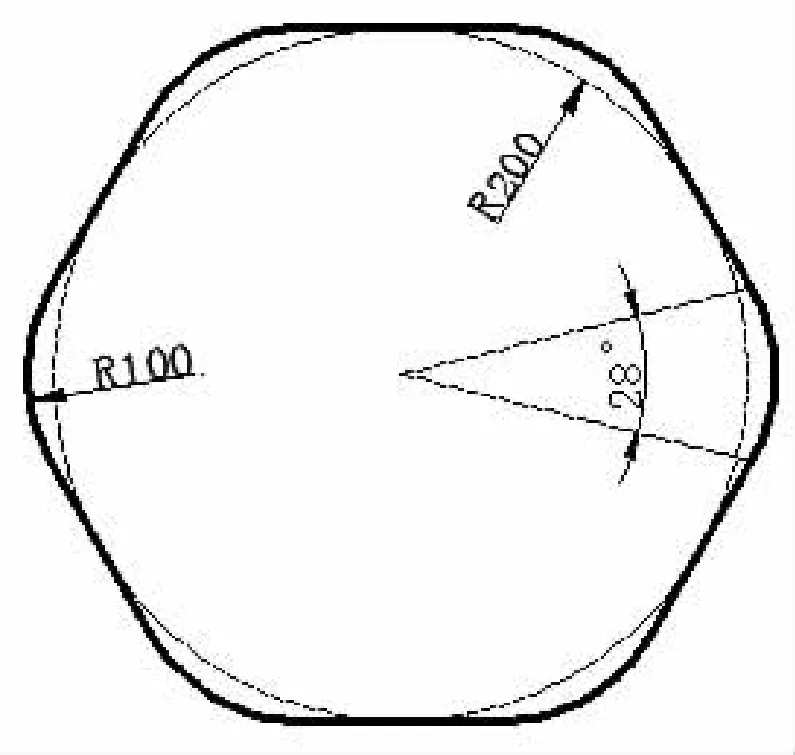
圖4 接觸曲線形狀參數
2.2 公式分析
根據模型參數,這些模型的接觸面為圓弧面和平面的組合面。如圖4所示的接觸曲線,這些接觸曲線由圓弧和直線段交替結合組成,且各段圓弧和直線的參數相同。

2.3 模型的有限元分析計算
繞繩與卷筒是柔—剛性面面接觸問題,分別將各個導入的模型在ANSYS WORKBENCH中設置好接觸參數、摩擦系數,繞繩一端施加1000N拉力,另一端設置為固定約束,將轉筒固定,劃分好網格,進行結構非線性分析。求得纏繞包角為120°時繞繩截面上的等效應力分布如圖5所示,用探針probe分別探測出纏繞線繩在各個不同纏繞包角時的緊邊等效應力和松邊等效應力,結果如圖5、圖7所示,并將所得的結果列在表1中。
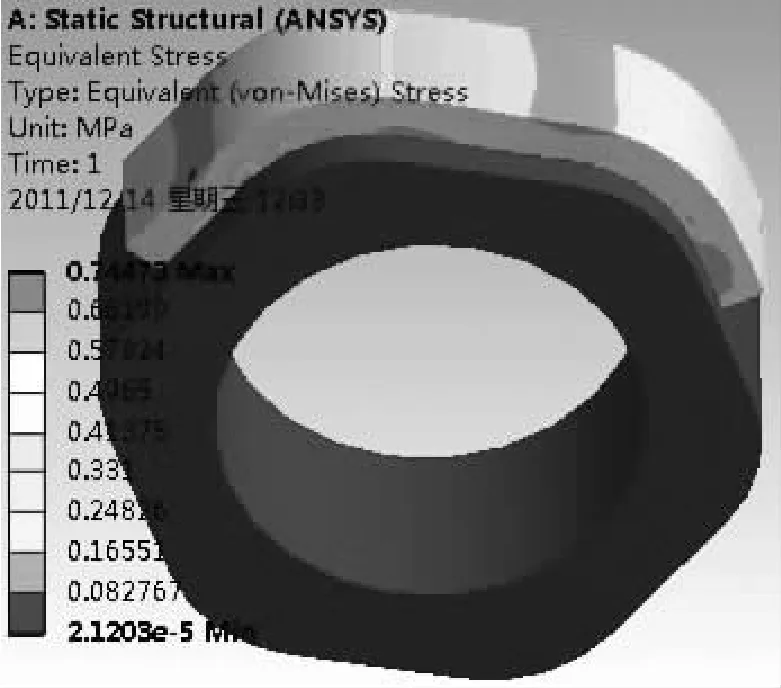
圖5 卷筒纏繞等效應力圖

圖6 纏繞包角為60°、120°、180°時線繩兩端的等效應力值

圖7 纏繞包角為240°、300°、360°時線繩兩端的等效應力值
2.4 計算結果分析
由上述知,張緊力的計算公式為:F2≈1000/e0.3α。用數學分析軟件Matlab繪制出此公式的曲線圖,如圖8所示。x軸方向表示接觸時圓弧段參與的包角,y軸方向是繞繩的等效應力。將表1中所得的結果點描在圖8等效應力曲線圖中,如圖所示圓圈點即為有限元分析的結果。
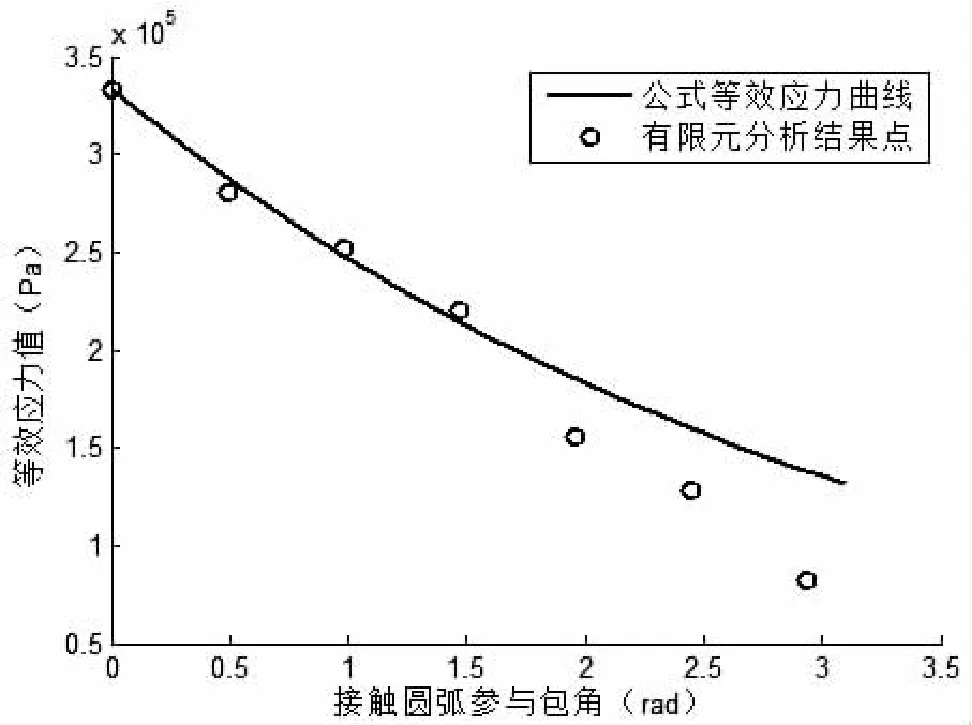
圖8 公式與有限元分析計算結果比較
從圖8分析可看出,有限元分析計算的結果和公式計算的結果在一定范圍內有一定程度的相符性。由此可知上述介紹的廣義歐拉公式在一定范圍內可以指導實際的工程應用。
3 結論
本文運用有限元法對模型進行計算分析,與公式計算所得的結果對比,借用數學分析軟件Matlab將它們繪制在一張圖上,直觀地進行比較。
由結果比較可知,運用ANSYS WORKBENCH有限元計算的結果和公式計算所得的結果在接觸圓弧參與的包角較小時,兩者的結果比較相符;圓弧參與的包角較大時,兩者的結果之間有一定的誤差。故本文介紹的纏繞于一般曲面體上的廣義歐拉公式在一定范圍內可以指導實際的工程應用,可以減少我們在遇到此類問題時計算張緊力時的誤差,比運用經典歐拉公式計算的結果更接近實際。所以上述介紹的纏繞于一般曲面體上的廣義歐拉公式具有更普遍的實用意義。
[1]楊可楨.機械設計基礎[M].北京:高等教育出版社,1989.
[2]楊景慧,陸玉,唐蓉城.機械設計(機械類)[M].北京:機械工業出版社,1995.
[3]曹助家,顧占山.歐拉公式在機械設計中的應用[J].機械制造,1994.

