滬深股市指數收益率波動性的實證分析

冷 軍

0 引言

隨著全球經濟一體化的進程，我國股市也越來越因為對全球經濟的敏感反應而呈現出不穩定和風險。尤其是2008年以來，金融危機席卷全球，使全球經濟迅速下滑，全球主要股市均出現了異常的波動，各個國家都把金融風險管理放到了極其重要的位置。股指收益率的波動性可以作為一種度量金融風險的手段。因此，對我國滬深股票市場股指收益率的波動性的研究，在理論和現實兩方面均具有十分重要的意義。已有的研究主要是基于收益率殘差分布服從條件正態分布對我國股票市場收益率進行實證分析。本文基于廣義誤差分布（GED），利用GARCH族模型，選取了1995年至2011年近16年的數據，對我國股票市場的收益率波動性進行長期的分析。本文通過實證分析發現采用廣義誤差分布時（GED），GARCH模型對我國股票市場的收益率波動性擬合的更好。

1 研究方法

ARCH模型已被廣泛地認為是目前最能集中地反映方差變化特點的模型，因而在經濟時間序列的分析中得到了廣泛應用。在恩格爾的ARCH模型基礎上，又有其他學者提出了GARCH、EGARCH、CGARCH以及GARCH-M等改進模型（一般合成為GARCH族模型），因其各自具有不同的特性，本文運用這些模型從不同的視角揭示我國股票市場指數收益率的波動性狀況。

2 數據描述及檢驗

2.1 數據描述

本文以上證綜合指數和深圳綜合指數為代表，研究我國股票市場指數收益率波動性特征。盡管上海交易所從1990年12月開始發布上證綜合指數，深圳交易所從1991年4月開始發布深證綜合指數，但是由于我國1995年5月1日開始實行5天工作日制，因此，我國股市交易也從1995年5月2日開始由一周6個交易日改為一周5個交易日，因此，為了時間序列的周期一致，本文選取1995年5月2日至2011年2月28日間每一交易日的日收盤價作為樣本，共3839個交易數據（數據來源于大智慧軟件），構成的時間序列分別為{SHP}和{SZP},對我A國股票市場近十六來的運行狀況進行研究。在這一樣本期內，我國股市經歷了2001年至2005年長達4年的熊市，2005年至2007年的大牛市以及之后持續的熊市；同樣，也經歷了我國股市國有股減持即股權分置改革，以及2008年以來的席卷全球的金融危機。因此，基于這么長的樣本期來對我國滬深兩地股市指數收益率的波動性進行研究，具有較好的代表性。圖1為樣本期內上證綜指和深圳綜指的走勢圖。

圖1 1995.5至2011.2上證綜指和深證綜指走勢

股市日收益率采用股價指數的一個對數差分來衡量，設Pt為當天的收盤指數，Pt-1為前一天市場的收盤指數，則可以將股票指數的收益率為：

根據上述公式，在滬深綜指時間序列分別為{SHP}和{SZP}的基礎上，構建了分表代表滬深兩地綜指日收益率的時間序列{SHR}和{SZR}。圖2為上證綜指和深圳綜指日收益率走勢圖。從圖中可以看出，上證綜指和深證綜指的收益率的波動都表現出明顯的時變性、突發性、與集聚性特征。

圖2 上證綜指和深圳綜指日收益率走勢圖

2.2 正態性檢驗

圖3 滬深綜指收益率的數據特征（左圖為滬市，右圖為深市）

通過eviews對上證綜指日收益率時間序列和深證綜指日收益率時間序列分別做描述性統計。獲得如圖3所示的兩指數日收益率的直方圖。由圖3可知，上證綜指收益率從的平均（Mean）小于深證綜指收益率，偏度（Skewness）和峰度（Kurtosis）都大于深證綜指收益率，另外，兩地股市的JB統計量均非常大且其P為0.00000。由于對稱分布的偏度等于0，而上證綜指收益率的偏度是正值，說明上海股市的收益率是向右偏斜的，而深證綜指收益率的偏度是負值，說明是向左偏斜的。正態分布的峰度等于3，而滬深兩地股市的綜指收益率的峰度均遠遠大于3，表明滬深兩地股市的收益率均顯著不服從正態分布，且具有較為明顯的“尖峰厚尾”。

2.3 平穩性檢驗

圖4 上證綜指日收益率序列{SHR}（左）和深證綜指日收益率序列{SZR}（右）的ADF檢驗

對上證綜指日收益率序列{SHR}做ADF檢驗，如上圖4所示，所得檢驗統計量為-60.55417，伴隨概率為0.0001，且1%顯著性水平下的MacKinnon臨界值為-3.431868，因此拒絕序列存在單位根的假設，該序列是平穩序列。同樣可驗證深證綜指日收益率序列{SZR}序列也是平穩序列。

3 實證結果及分析

根據序列的自相關和偏自相關分析圖，上證綜指日收益率序列{shr}存在滯后11階偏自相關，而深證綜指日收益序列{szr}存在滯后15階偏自相關，又根據簡單實用原則，均值方程分別設為

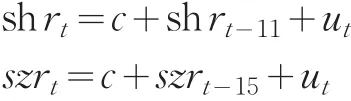
下面根據方差方程的設定不同，采用不同的模型對我國滬深股市綜指日收益率的波動性進行研究，模型參數估計方法采用擬極大似然估計法，得到穩健標準差。

3.1 GARCH(1,1)模型

模型各參數估計結果見表1。

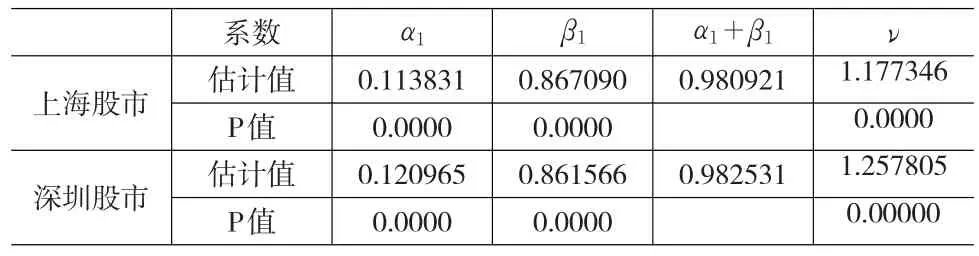
表1 滬深股市收益率GARCH(1,1)模型估計結果

從表1可知，滬深股市尾部厚度的度量參賽ν的估計值分別是1.177346和1.257805，均小于2，且隨行概率均非常低，說明收益率不具有正態分布（正態分布ν=2）的特性，呈現出后尾性，GED分布擬合數據效果良好。上海股市和深圳股市的方差方程中殘差平方項的系數α1和方差項的系數β1均是正數，且在0.001水平上顯著，反映了異方差性和波動聚集性的存在；而系數之和α1+β1均接近于1，則說明了兩市股價具有很強的波動持續性。對兩地股市的方差方程系數和進行Wald檢驗結果如表2：

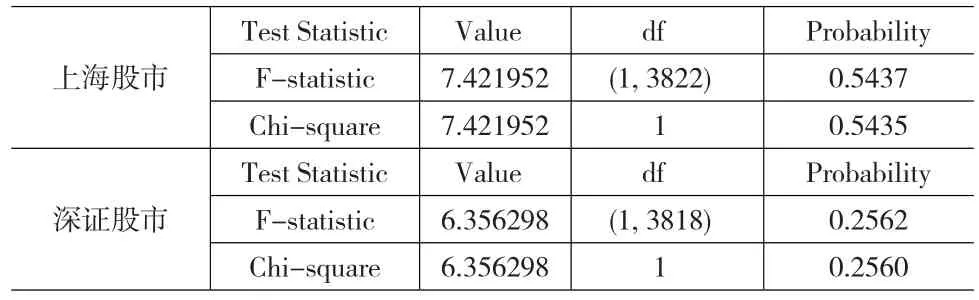
表2 兩地股市方差方程系數和的wald檢驗

由滬深兩地股市指數收益率方差方程系數和的wald檢驗結果可知，由于F檢驗和卡方檢驗的隨行概率均大于顯著性水平，因此接受系數和為1的原假設，表明波動性沖擊具有持久性的效應，且過去的沖擊對未來波動的影響衰減得十分緩慢。另外，通過對殘差項進行ARCH-LM檢驗，發現不存在ARCH效應，因此利用GARCH(1,1)模型描述滬深股市指數收益率波動的效果較好。

3.2 基于GJR-GRACH(1,1)模型的杠桿效應研究

GJR-GRACH(1,1)的方差形式為：

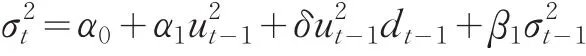
模型各參數估計結果見表3。

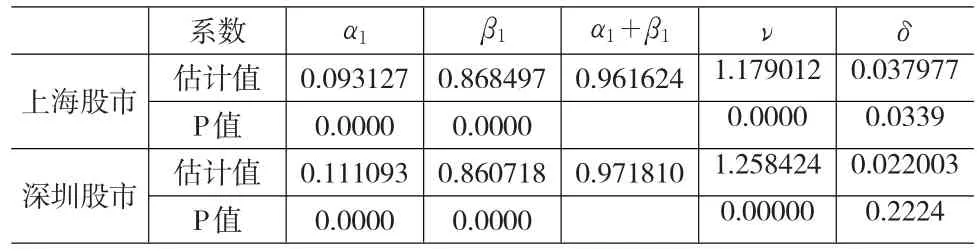
表3 滬深股市收益率GJR-GRACH(1,1)模型估計結果

由估計結果可知，上海股市綜指收益率的δ在5%的水平上顯著，而深圳股市綜指收益率的δ并不是不顯著的，表明在樣本期內上海股市的杠桿效應明顯，而深圳股票市場的杠桿效應不十分明顯。但兩市場的δ都為正，說明利空消息影響大于利好消息影響。

3.3 E-GARCH（Exponential GARCH）模型

為進一步驗證杠桿效應，用EGARCH（1，1）模型做實證檢驗，結果如下表4所示：

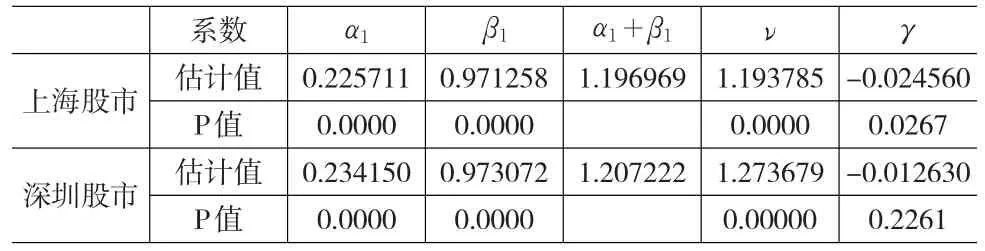
表4 滬深股市收益率利用E-GARCH(1,1)模型的估計結果

由表4可知，滬深兩地股市綜指收益率的非對稱系數γ均為負，說明利空消息比利好消息產生更大的波動，其中，上海股市在5%的水平上顯著，深圳股市不顯著。上海股市，γ=-0.024560，則正的沖擊對波動的影響比負的沖擊對波動的影響小，當ut-1＞0時，有一個α1+γ=0.201151倍沖擊，當ut-1＜0時，有一個α1+γ=0.250271倍的沖擊。且參數統計量均顯著，說明對利好和利空消息對股價波動性影響較大。 α1和 β1都很顯著，但 α1+β1＞1，表明收益率波動不會衰減，波動最為劇烈，不滿足平穩性條件。

3.4 GARCH-M模型

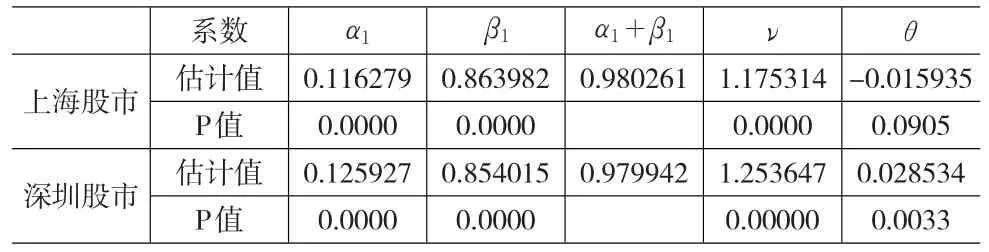
表5 滬深股市收益率利用GARCH-M(1,1)模型的估計結果

由表5可知，上海市場的風險溢價系數θ為-0.015935，且在10%的水平上顯著，符號為負，說明上海股市的投資者的收益期望與市場波動之間呈弱負相關，但絕對值很小，投資者對市場風險是弱偏好的，有一定的投機成分，這從另一個側面反映了我國股票市場仍是一個不成熟的新興資本市場，股票市場中仍有一定的投機現象，而這種投機性的存在又會使得股票價格的波動更加劇烈。另一方面，深圳市場的風險溢價系數θ為0.028534，符號為正，說明收益率與風險成正向變化，投資者對市場風險是厭惡，對于波動需要一定的風險補償，但絕對值也很小，僅為0.080027，說明風險厭惡程度很小，市場的投機現象沒有滬市的嚴重。

4 結論

本文根據不同模型的特點，分別采用GARCH模型族中 的 GARCH(1,1)、GJR-GRACH(1,1)、EGARCH(1,1)以 及GARCH(1,1)-M等模型，從多個視角我國股票市場指數收益率的波動性狀況進行分析。實證研究結果表明：

（1）和發達國家的股票市場一樣，我國股票市場指數收益率也存在著波動的聚集性、爆發性、持久性以及均值恢復性。

（2）我國上證指數收益率波動性存在明顯的非對稱性，杠桿效應明顯，利好和利空消息的發布對股票市場指數收益率的波動性會顯著的影響。這與朱均均、謝識予（2011）、周少甫（2005）的研究結果基本一致。而深證指數收益率的非對稱性、杠桿效應均不顯著，利好和利空消息對股指收益率的波動性影響不顯著。這與周少甫（2005）發現的滬深兩市均具有顯著的非對稱性的研究結果有所不同。

（3）我國滬深股票市場總體上不存在顯著的風險——收益權衡關系，投資者總體上趨于中性，其中上海市場投資者有點風險弱偏好，深圳市場有一定的風險厭惡，對承擔風險要求一定的補償。這與周少甫（2005）、陳雄兵、張宗成（2008）的研究結果有所不同，但在滬市中的投機性要比深市嚴重的結果與周少甫（2005）的結論一致。這意味著我國股票市場雖然與發達國家股市之間雖然仍存在比較大的差距，但已有很大的改善，投機現象有所減少。

[1]藩越.成交量的GARCH修正模型在股市波動中的應用[J].統計與決策,2004,(8).

[2]周少甫,袁興興.我國股票市場波動非對稱性的實證研究[J].當代經濟管理,2005,（6）.

[3]陳雄兵,張宗成.基于修正GARCH模型的中國股市收益率與波動周內效應實證研究[J].中國管理科學,2008,(8).

[4]高鐵梅.計量經濟分析方法與建模（第二版）[M].北京:清華大學出版社,2009,(5).

[5]陳守東,馬輝,才元.上海證券市場分階段收益率與波動性的特征分析[J].吉林大學學報(社會科學版),2006,(7).

[6]中國股市波動率的雙重不對稱性及其解釋——基于MS-TGARCH模型的MCMC估計和分析[J].金融研究,2011,(3).

[7]馬慧敏.滬市A股弱勢有效性實證研究[J].求索，2011，（8）.