變深度水下發射系統內彈道實驗研究①

呂 翔，李 江，陳 劍，何國強，梁 材，靳成學

(1.西北工業大學 燃燒、熱結構與內流場重點實驗室，西安 710072;2.中國船舶重工集團713所，鄭州 450015)

0 引言

為提高水下發射系統的作戰反應速度，使潛載導彈能夠在不同水下深度有效發射，目前普遍采用了變深度發射技術［1－4］。國外采用變深度發射技術的潛載導彈主要有美國的“三叉戟Ⅱ”(發射深度19.2～37.2 m)和法國的M51導彈(最大發射深度為40 m)。變深度發射需要發射動力系統具備發射能量可調的基本能力［4－7］，以保證導彈能夠在不同的發射深度、以不同的發射速度離開發射筒。變深度發射技術研究需要開展大量的水下發射實驗來獲得足夠的有效數據進行建模分析，以研究發射系統能量調節［4－5］、發射系統內彈道［3，6－7］、導彈結構動力學響應和導彈的水下動力學［8］等。

開展變深度水下發射實驗研究的方法之一是進行全尺寸模型實驗，例如法國建造了直徑φ30 m、深度50 m的巨大水池開展M51導彈的變深度發射實驗研究。該方法的不足之處是規模龐大、實驗周期長和費用高，難以開展大量的細致深入研究。目前還未見國外關于變深度水下發射系統模擬實驗的相關報道。

本文采用模擬實驗裝置開展了變深度水下發射實驗，研究不同發射深度和發射速度下發射系統內彈道，為發射系統設計提供參考。

1 實驗裝置及實驗方法

變深度水下發射實驗裝置如圖1所示，系統主要包括:燃氣－蒸汽式發射動力裝置［5］、發射筒、縮比模型彈和變深度模擬裝置。其中發射動力裝置由燃氣發生器、冷卻水噴注器和摻混器組成，其基本原理是通過調節熱燃氣和冷卻水的流量以適應不同的發射深度和發射速度。發射筒出口處設置有隔水膜，用以在發射前將模型彈和海水隔開，模型彈運動到發射筒口時會觸發隔水膜破裂。與發射筒相連的變深度模擬裝置內有一定深度的海水，以模擬導彈在水下發射過程中所受的阻力，目前能夠模擬的深度最大為100 m。

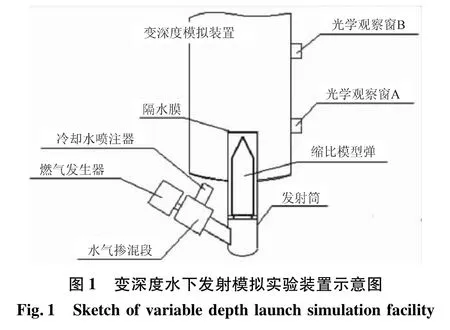
在變深度模擬裝置側壁沿高度方向設置一定數量的光學觀察窗，以觀測模型彈在水下的運動過程。其中觀察窗A位置正對發射筒口處，觀察窗B位于模型彈完全出筒時刻正對彈頭的位置。調試實驗證明［9］，在觀察窗B處利用高速攝影能夠有效捕捉到模型彈完全出筒過程，并計算出模型彈的發射速度。目前采用拍攝速度最大為2 000 fps的Mega Speed MS50K高速攝影系統進行模型彈的運動分析。為準確獲得模型彈的發射速度，在彈身和窗口B處均按一定的標準尺寸設有彩色標識，用于進行模型彈發射速度的有效判讀［9］。在燃氣發生器、冷卻水噴注器、摻混器和發射筒上均設有一定的壓強測點，實驗中采用采樣率為5 kHz的并行數據采集系統來獲得內彈道曲線。

在變深度模擬發射實驗前，首先根據理論計算［3］和有用能調節裝置實驗結果選擇合適的燃氣發生器流量和冷卻水流量，以確保發射速度滿足實驗要求。有用能調節裝置的燃氣發生器點火后，冷卻水噴注到熱燃氣中并與之摻混，形成的高溫蒸汽進入到發射筒底部，當建立足夠的發射筒底部壓強后模型彈開始運動，并觸發筒口的隔水膜破裂，隨后模型彈進入到海水內開始水下運動過程，最終由回收機構完成模型彈的止落回收。

按表1所示實驗工況開展了變深度模擬發射實驗，模擬的發射深度H為30 m和60 m，設計發射速度vD=15～45 m/s。其中發射速度設計值vD根據變深度發射系統內彈道理論分析模型［2］計算得到。

表1 變深度水下發射實驗工況Table 1 Experiments conditions for variable depth launch simulation

2 實驗結果及分析

2.1 高速攝影圖像處理結果分析

圖2給出了實驗2模型彈完全出筒瞬間2個典型時刻下的高速攝影圖像，表2則給出了按照圖像處理結果得到的實際發射速度vC及其不確定度u(vC)。關于圖像處理方法及發射速度不確定度計算方法的詳細說明見參考文獻［9］。

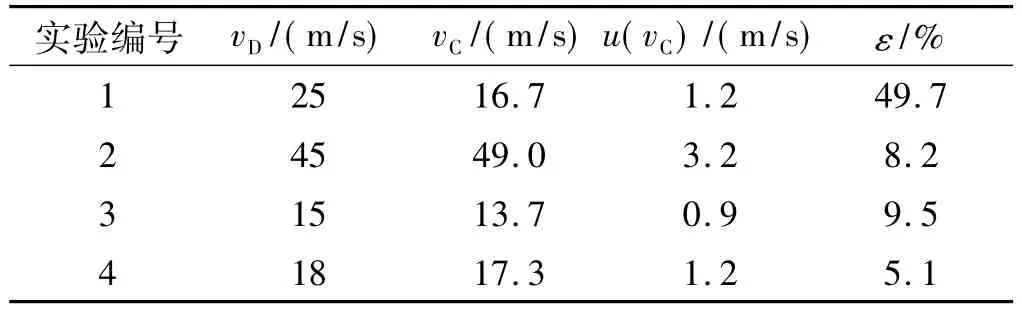
表2 基于數字圖像處理的發射速度Table 2 Launching velocity from digital image processing

由表2可看出，實驗1發射速度的設計值vD與實際值vC相差較大，相對誤差ε為49.7%;實驗2～實驗4的發射速度設計值與實驗結果的最大相對誤差ε均小于10%。需要說明的是，實驗1采用了基于全尺寸導彈水下發射實驗結果所建立的內彈道設計模型，而實驗2～實驗4則是采用基于實驗1結果修正的內彈道計算模型。由于實驗裝置與全尺寸發射裝置的工作過程完全相同，其差別主要在于尺寸不同。這說明在進行實驗裝置縮比設計時存在較大的尺寸效應。通過分析內彈道設計模型發現，尺寸效應的主要影響因素在于發射裝置的能量利用效率［2］。

2.2 壓強曲線分析

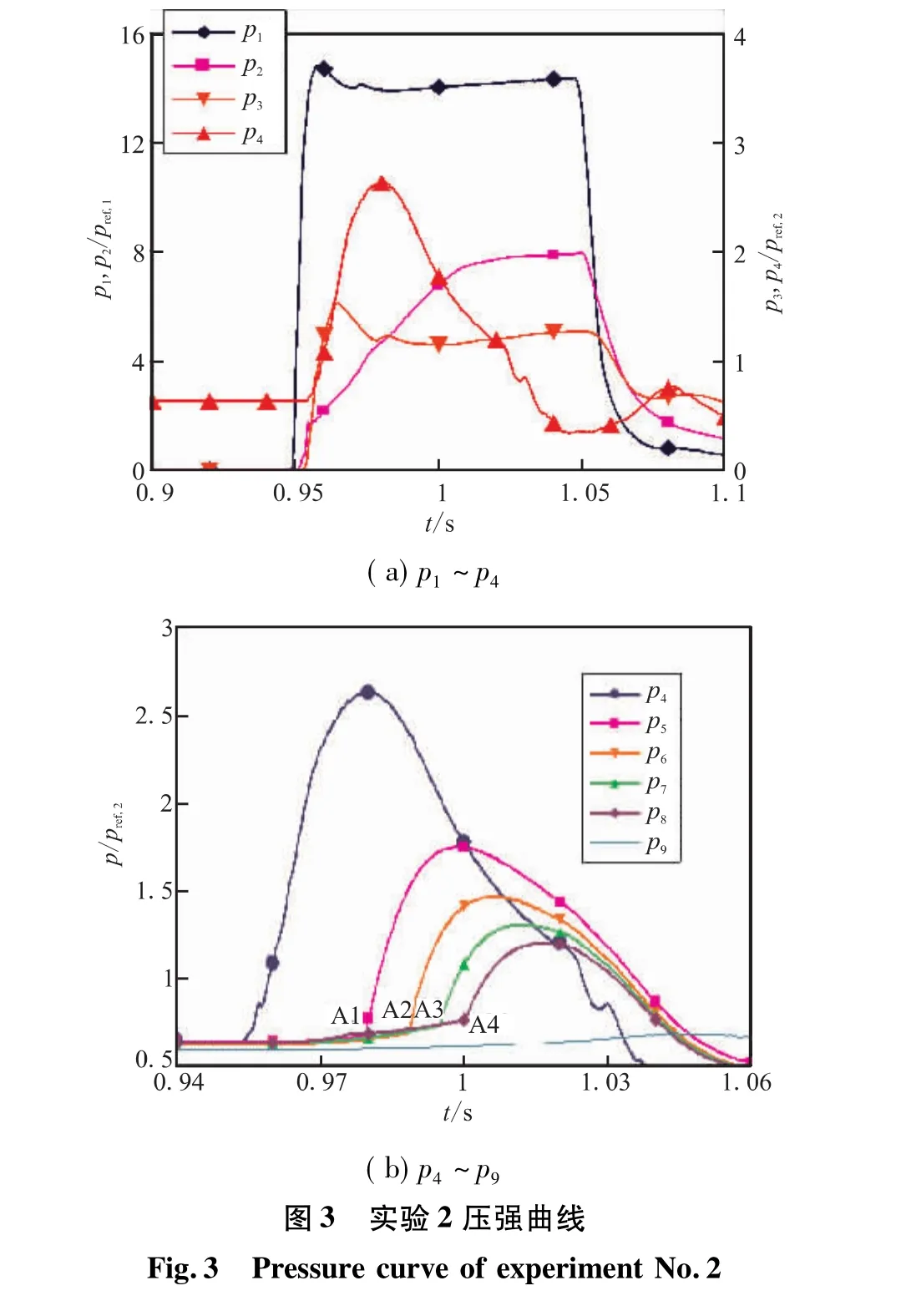
由于實驗1的設計狀態與實際偏離較大，為便于比較分析實驗結果，選取實驗2作為典型工況進行研究。圖3給出了實驗2的壓強曲線，其中p1為燃氣發生器室壓，p2為噴注器壓強，p3為摻混器壓強，p4位于發射筒底部，p5～p8為發射筒上沿高度方向的壓強分布，p9為模型彈迎水截面所受的壓強。

從發射筒上部壓強曲線p5～p8可看出，模型彈開始運動時各測點壓強平緩上升，隨后p5～p8依次出現壓強突升的拐點，如圖3(b)所示的A1～A4各點。在拐點處壓強突然上升，這表明模型彈尾部已經運動至該測點位置，導致測點與發射筒底部完全連通。因而，可將此拐點作為模型彈的典型運動時刻，用于發射筒內彈道分析和模型彈在發射筒內運動規律分析。

在模型彈開始運動之前，發射筒上部壓強p5～p8與發射筒底部壓強p4是完全隔離的，并保持恒定。當模型彈開始向上運動時，發射筒內彈尾平面上方空腔的氣體開始受到壓縮作用，其壓強逐漸上升，在內彈道曲線上表現為各測點壓強開始上升。由于p5接近于模型彈的底部，因而當p5開始上升的時刻可作為模型彈發射的起始時刻t0，由此可確定出實驗2的發射起始時刻t0=0.960 s。利用此方法同樣可確定出其他各次實驗的模型彈發射起始時刻。

2.3 運動方程分析與求解

模型彈在發射筒內運動時受到的作用力包括重力、發射驅動力和阻力。其中發射驅動力由發射筒底部壓強產生，阻力不僅包括迎水面上產生的水壓阻力，還包括發射筒壁面、發射筒內氣體及海水等作用于模型彈表面的運動摩擦阻力f。

根據牛頓第二運動定律，模型彈的加速度為

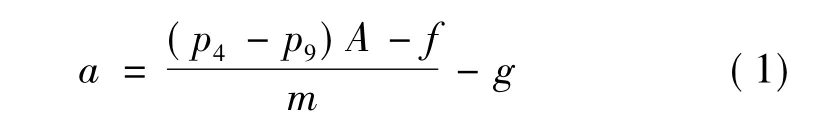
式中 A為模型彈的橫截面積;m為模型彈質量;g為重力加速度常數。

則模型彈的速度v和位移s可表示為

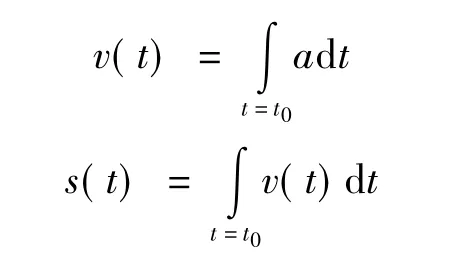
因各項摩擦阻力難以直接計算，本文定義如下所示的運動摩擦系數β來計算總運動摩擦阻力f:

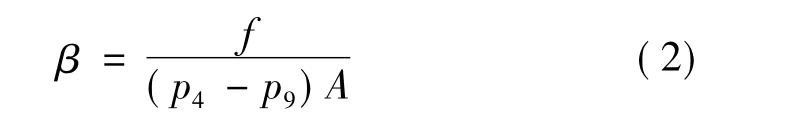
理想情況下，β=0表示沒有任何運動摩擦阻力。引入運動摩擦系數后，模型彈的實際加速度可表示為

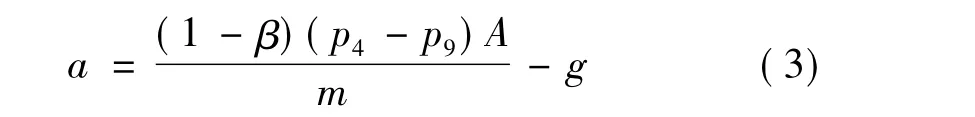
將式(3)代入模型彈的速度和位移計算式中可得

摩擦系數β與模型彈的實時運動速度v(t)密切相關，并存在復雜的非線性函數關系式，因而方程(4)、(5)組成了一個非常復雜的非線性方程組，求解難度較大。為了適當的簡化求解過程，本文假定在單次發射過程中摩擦系數β保持恒定，只與模型彈的出筒速度相關。

在上述方程中未知參量包括模型彈的運動摩擦系數β和模型彈運動的終點時刻tE，為了求解方程組需要附加2個約束條件。

由于模型彈在完全出筒時刻的位移應為設計值1.55 m，因此式(5)的終點約束條件為

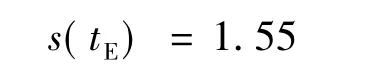
對于各次實驗來說，壓強測點p5和p8對應的間距是由實驗裝置設計狀態所唯一確定的，而模型彈在兩者之間的運動時間差ΔT5-8可由發射筒內彈道曲線分析獲得(如圖3)。

根據模型彈運動方程及其約束條件的分析，建立了如圖4所示的求解方法。

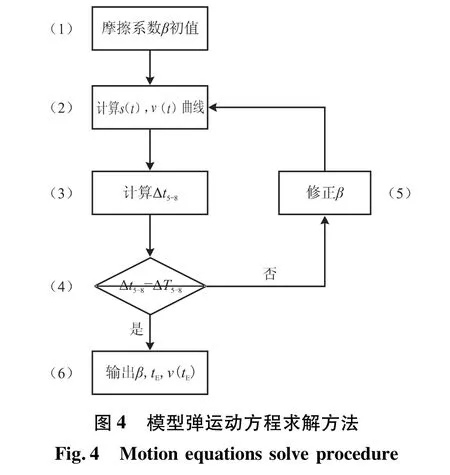
步驟2中計算s(t)和v(t)曲線時利用模型彈運動終點約束條件，利用4點的Simpson方法［10］在時間步長上積分，直到s(t)=1.55。步驟3中計算Δt5-8，首先在步驟2獲得的s(t)曲線中查找p5和p8位置所對應的時刻 tp5和 tp8，則 Δt5-8=tp8－tp5。步驟4中 ΔT5-8由實驗曲線獲得。步驟5中采用了二分法對運動摩擦系數β進行修正，當Δt5-8＞ΔT5-8時表明假定的摩擦系數β過大，模型彈運動速度小于實驗值，需要調小摩擦系數β，反之則需要調大摩擦系數β。

利用圖4所示的求解方法，對4次實驗結果進行了計算分析，得到了如表3所示的不同實驗發射速度vB和運動摩擦系數β。通過擬合得到了如式(6)所示運動摩擦系數β與發射速度vB的函數關系，擬合結果與實驗結果的對比見圖5。

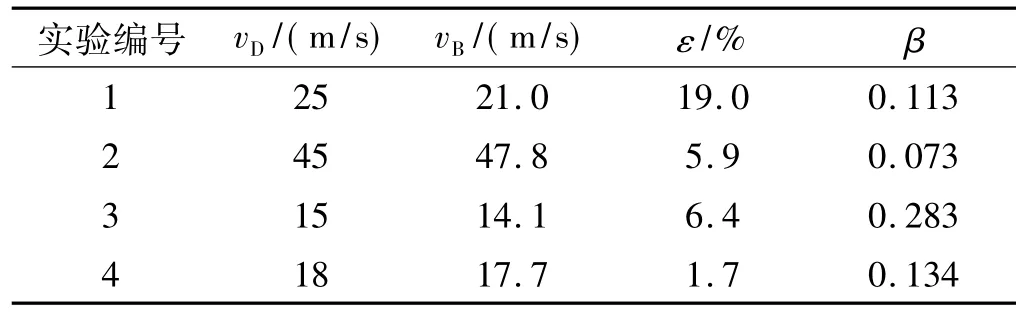
表3 模型彈運動規律分析結果Table 3 Subscale missile movement analysis results

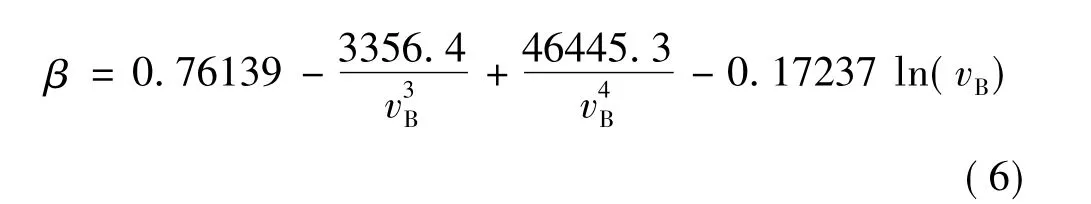
表3所示計算結果表明，運動摩擦系數隨發射速度的增大而減小，實驗值最大為0.283，最小為0.073。綜合對比實驗1、實驗3和實驗4的運動摩擦系數可發現，發射速度由17.7 m/s變為21.0 m/s時，運動摩擦系數的絕對變化量為0.031，而發射速度由17.7 m/s變為14.1 m/s時，運動摩擦系數的絕對變化量達到了0.149。這說明存在影響運動摩擦系數的臨界發射速度，當發射速度低于臨界值時運動摩擦系數變化劇烈，而當發射速度高于臨界值時運動摩擦系數變化平緩。根據圖5所示運動摩擦系數與發射速度的關系，可推測影響運動摩擦系數的臨界發射速度為18～20 m/s。當發射速度小于臨界值時，由于運動摩擦系數變化劇烈，為了保證導彈發射初速度的精確性，需要對發射動力裝置的內彈道提出較高的控制精度要求。

2.4 發射速度對比

表4給出了發射速度的理論設計值vD、高速攝影分析結果vC和內彈道分析結果vB。可看出，除了實驗1的結果存在較大差異外，其他各次實驗中不同方法得到的發射速度吻合較好。實驗2～實驗4中，發射速度的設計值vD與內彈道分析結果vB的最大相對誤差εDB=6.4%。實驗2～實驗4中，通過發射筒內彈道分析得到的發射速度vB均位于高速攝影結果vC的不確定區間內，最大相對誤差εCB=2.8%，這說明2種完全不同的分析方法能夠相互印證。同時也說明，本文所提出的“發射過程中摩擦系數β恒定并且只與模型彈出筒速度相關”這一假設用于內彈道分析是可行的。與考慮發射過程中各種阻力作用的復雜計算模型相比，這將在一定程度上簡化發射動力系統的內彈道計算分析模型。

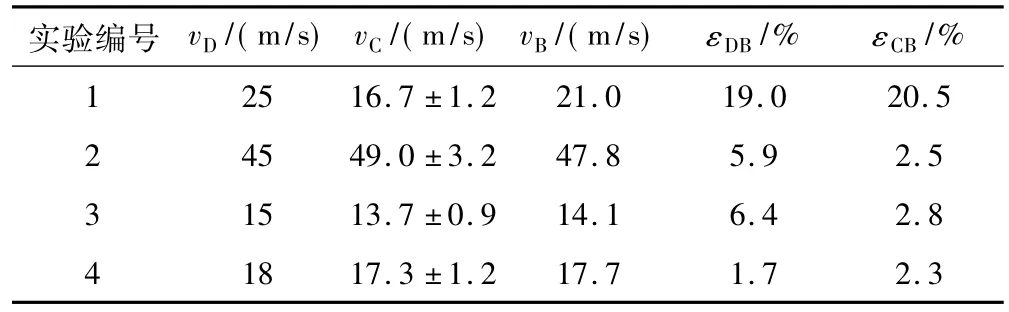
表4 發射速度對比Table 4 Comparison of launching velocity

實驗1發射速度的高速攝影分析結果vC和內彈道分析結果vB相對誤差εCB=20.5%，遠遠大于其他3次實驗結果。實驗1作為其他各次實驗的基礎，在高速攝影測量方法和成像質量等方面會存在需要改進的地方，從而導致速度測量結果出現偏差。而后續實驗均是在前一次實驗的基礎上不斷改進和完善，從而保證了高速攝影分析結果具有較高的準確性。更為重要的一點是，彈道分析時采用了出筒位移設計值、發射筒上典型測壓點坐標等多個確切尺寸參數作為約束條件來計算發射速度，利用此方法得到的發射速度較高速攝影結果應當更為精確。

3 結論

(1)建立的變深度水下發射系統內彈道分析方法可簡化發射動力系統的內彈道計算分析模型，并能夠較好地獲得模型彈發射速度。

(2)利用全尺寸水下發射系統縮比設計變深度發射模擬實驗裝置時存在顯著的尺寸效應。

(3)基于實驗結果修正的變深度發射內彈道計算模型所獲得的發射速度，與發射筒內彈道分析結果的最大相對誤差為6.4%。

(4)模型彈在發射筒內運動摩擦系數隨發射速度的增大而降低。

(5)影響運動摩擦系數變化規律的臨界發射速度為18～20 m/s，當發射速度低于臨界值時需要提高發射動力裝置的內彈道控制精度。

［1］倪火才.潛載導彈水下發射技術的發展趨勢分析［J］.艦載武器，2001(1):8－16.

［2］趙險峰，王俊杰.潛地彈道導彈系統內彈道學［M］.哈爾濱工程大學出版社，2000.

［3］李咸海，王俊杰.潛地導彈發射動力系統［M］.哈爾濱工程大學出版社，2000.

［4］李悅，周儒榮.導彈變深度發射動力調節技術研究［J］.南京理工大學學報，2003，27(2):127－131.

［5］肖虎斌，趙世平.燃氣蒸汽式發射動力裝置復雜內流場數值模擬［J］.固體火箭技術，2009，32(4):392－395.

［6］Edquist C T.Prediction of the launch pulse for gas generator launched missiles［R］.AIAA－88－3290.

［7］Edquist C T，Romine G L.Canister gas dynamics of gas generator launched missiles［R］.AIAA－80－1186.

［8］CHENG Yong－sheng，LIU Hua.Mathematical modeling of fluid flows for underwater missile launch［C］//Conference of Global Chinese Scholars on Hydrodynamics，2006:492－497.

［9］呂翔，李江，魏祥庚，等.變深度模擬發射實驗導彈出筒速度測量方法［J］.固體火箭技術，2011，34(2):265－268.

［10］William H Press，Saul A Teukolsky，William T Vetterling，et al.Numerical recipes in C(Second Edition)［M］.Cambridge University Press，1992.