旋轉固體火箭發動機燃燒室內流場分析解①

劉平安，王 革，郜 冶

(哈爾濱工程大學航天工程系，哈爾濱 150001)

0 引言

旋轉過載引起固體火箭發動機性能的改變，一般有4種潛在的重要影響模式出現［1］:第1種模式是旋轉加速過載引起殼體和藥柱變形的力學模式(machanical mode);第2種為熱力學模式(thermodynamic mode)，其導致燃燒性能的改變;第3種為應力模式(stress mode)，其導致推進劑燃速發生變化;第4種模態就是氣動力模式(gas dynamic mode)，旋轉過載將引起燃燒室和噴管的流動性能發生改變［2－8］。文獻［9］研究了無限長圓柱形固體裝藥通道粘性不可壓縮氣體沿橫截面氣流切向速度分布的近似關系。對于有分布質量進入的旋轉圓管內，切向速度分布類似Rankine渦。國內在旋轉固體火箭發動機性能和流動特征方面也開展了廣泛的研究［10－12］。文獻［13－14］應用數值方法，研究了旋轉固體火箭發動機的內流場，分析了旋轉發動機內流場的分區特征和端面近軸區域的回流效應，研究了轉數對渦核結構及端面流場細微結構的影響。

本文旨在應用解析分析法求解旋轉情況下的發動機內部流場，分析旋轉和壁面質量注入對渦核結構的影響。

1 數學物理模型

1.1 物理模型

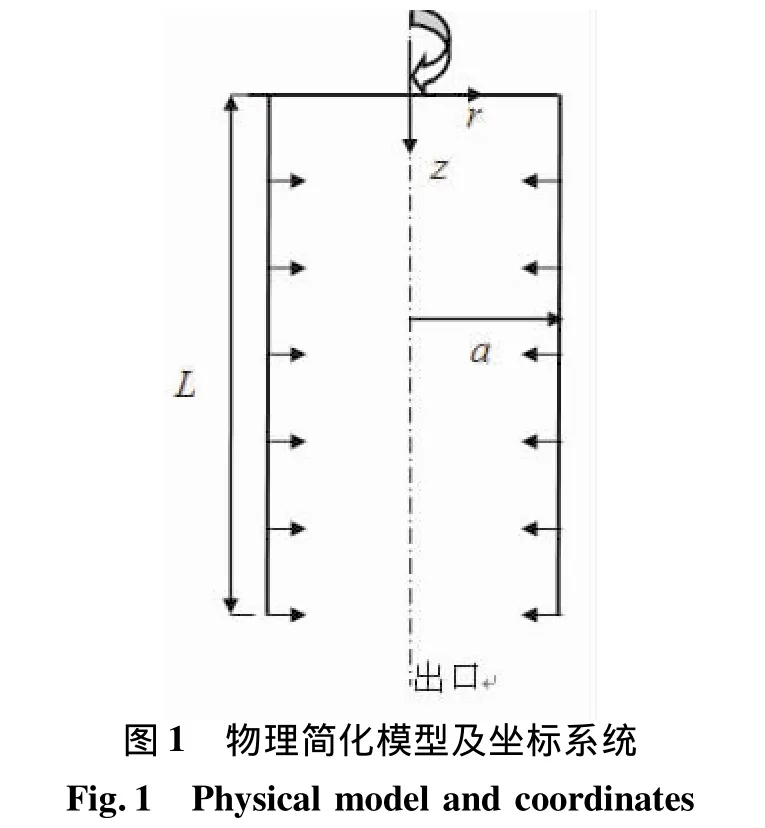
軸對稱管型裝藥內孔燃燒固體火箭發動機燃燒室通道空間的簡化模型如圖1所示，長為L，半徑為a，頭部封堵。燃燒室側壁面有流體均勻注入，注入速度為Vb，發動機轉速為ω，則側面切向速度U=ωa。

1.2 基本假設

由于發動機旋轉時，內流場變化較復雜，引入以下假設條件:

(1)流動處于穩定狀態;

(2)流體等溫不可壓;

(3)忽略體積力;

(4)粘性系數ν為常數;

(5)忽略頭部壁面摩擦影響。

1.3 控制方程

通用控制方程:

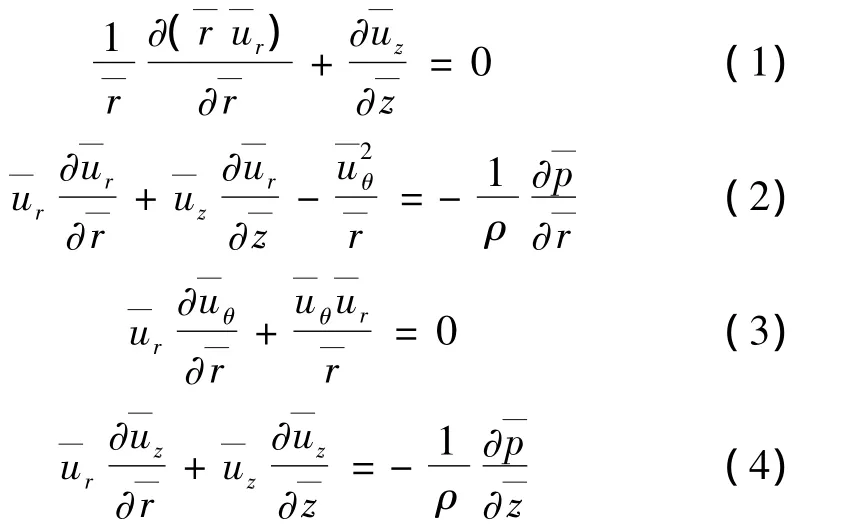
1.4 邊界條件

1.5 參數無量綱化

為了更簡潔地描述物理問題，下面將各參數無量綱化:

2 方程的解析求解

2.1 簡化方程

將式(3)無量綱化，有

2.2 求解方程

2.2.1 方程的通解

運用分離變量法，認為:

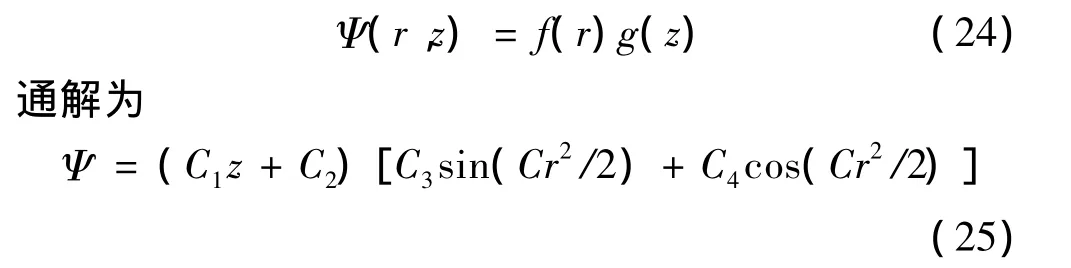
2.2.2 方程的特解

應用式(23)的邊界條件確定常數:

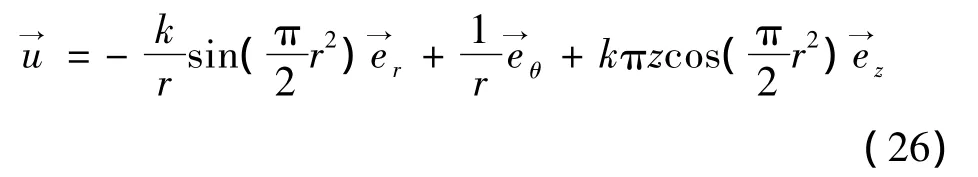
式(26)是滿足全部邊界條件的速度解。

2.3 修正切向動量方程

假設整個流場只存在自由渦，該假設雖然對徑向與軸向速度的分布影響很小，但明顯存在缺陷。完整的假設應包括外部自由渦與核心強制渦，核心強制渦的運動類似于剛體旋轉，由于軸附近粘性力的作用而產生。為了得到準確的切向速度分布，需修正切向動量方程，在式(3)中引入粘性項。修正后的切向動量方程無量綱形式為

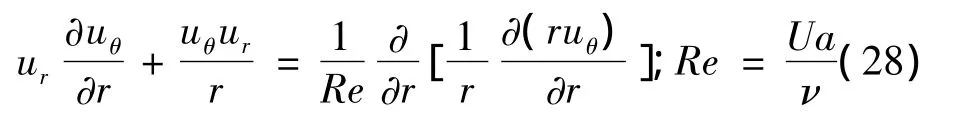
式中 Re為平均流動雷諾數。

令 uθ=uθ(r)，式(28)化為常微分方程:

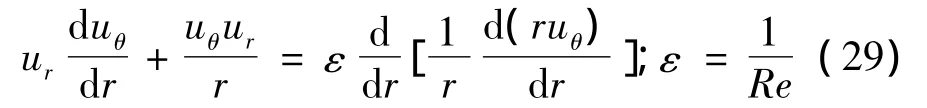
引入2個邊界條件:

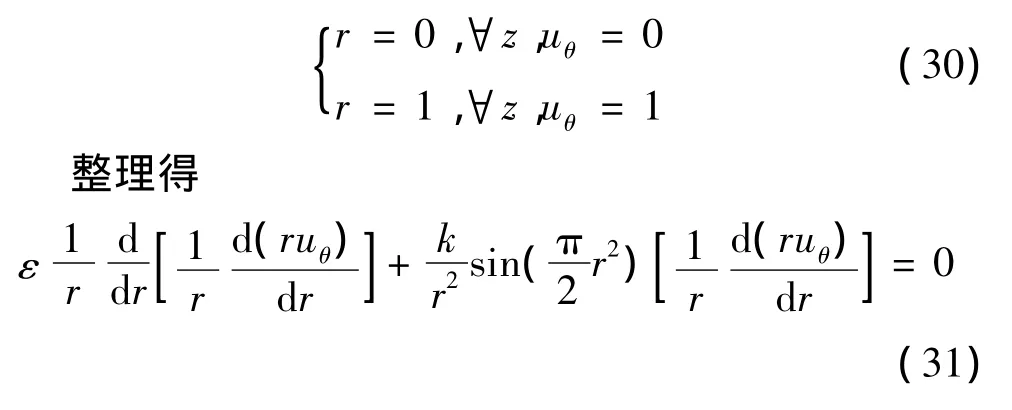
為了簡化方程，令:

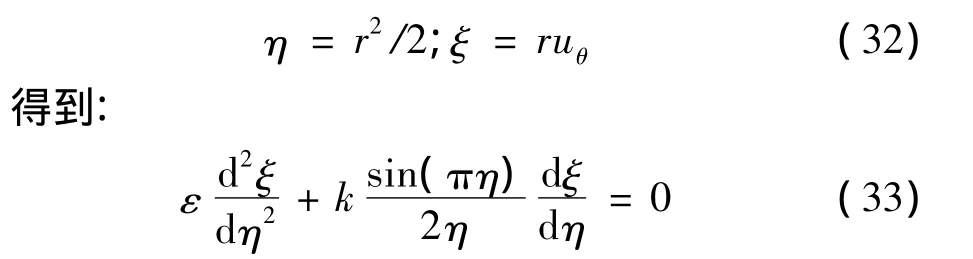
2.4 重新求解切向速度

實際情況中Re＞1 000，因此ε非常小，可作為攝動量，運用攝動法中的漸進展開匹配法求解切向速度:

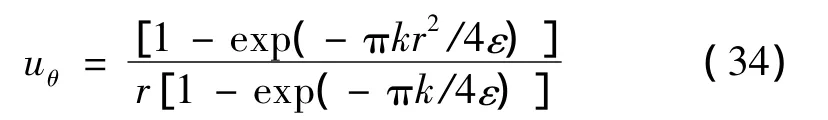
式(34)為切向速度的最終表達式。當ε→0時，切向速度與全場自由渦假設條件下得到的結果一致，即uθ=1/r。對于固定的 ε，當 r→0時，可將式(34)展開為

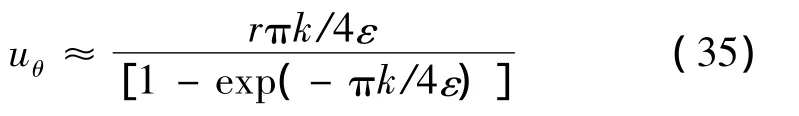
顯然，uθ與r成正比，說明核心區流體類似于剛體做繞軸轉動，這是由于集中的粘性力作用。應注意到，前面得到的解明顯受參數ε與k的影響，因此定義有效雷諾數ReV(注入雷諾數):

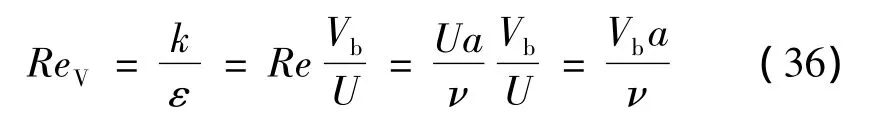
式(34)切向速度的表達式可寫成ReV的表達形式:

2.5 粘性渦核厚度

為了確定強制渦的影響區域，首先要確定渦核半徑r*。對式(34)求導可得，并令其等于0。

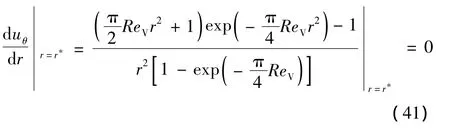
由此可得

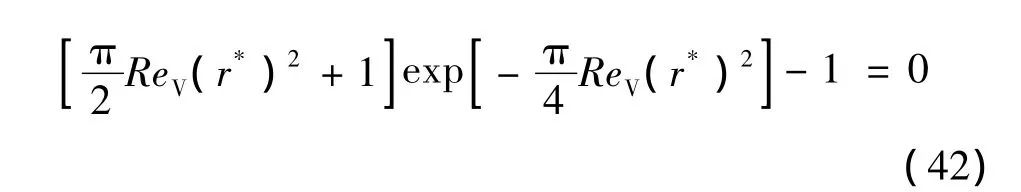
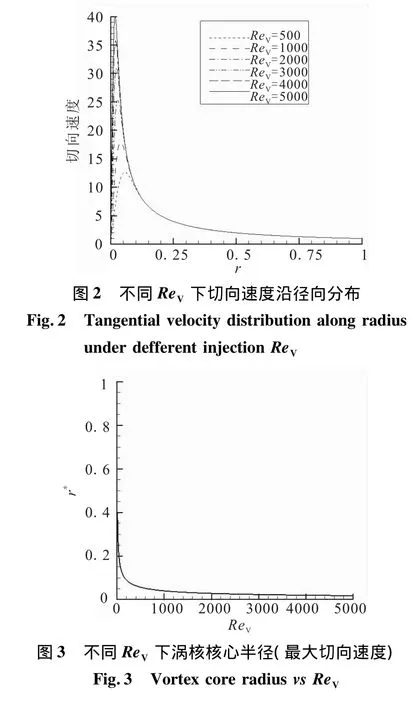
不同ReV下切向速度沿徑向分布見圖2;最大切向速度的位置，即渦核核心半徑r*隨ReV的變化見圖3。當ReV超過500時，其渦核半徑減小程度趨于平緩。小于500時，渦核半徑變化加大。當注入速度一定的情況下，湍流比層流的粘性系數大得多，對應的ReV相應減小。因此，湍流的渦核半徑比層流情況下大很多，湍流強度越大，對應的渦核區也就較大。

2.6 切向速度的近似關系

式(34)可寫成如下近似關系:

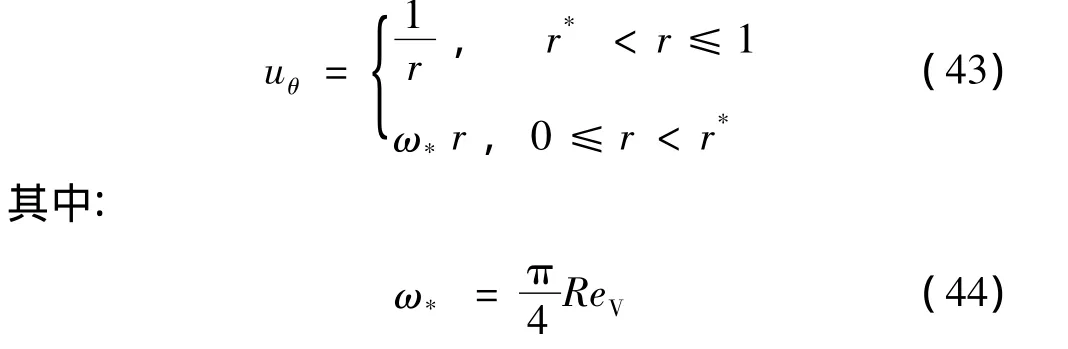
由r*處的連續條件ω*(r*2)=1可得

相應于式(43)，一般在ReV＞103的情況下，通道內不可壓縮燃氣的切向流動速度在2個區域內具有不同的特點，在小于r*的圓柱氣流核心區，切向速度呈“準固體”特征，其旋轉角速度ω*明顯超過通道旋轉角速度ω。而大于r*的區域切向流動為自由旋流。由于在旋轉角速度很高的情況下，不可壓縮的假設會帶來較大的誤差，因此對高速旋轉的通道，應考慮可壓縮性的修正。

2.7 切向速度的可壓縮性修正

文獻［9］分析了可壓縮氣體在旋轉通道內的切向速度橫截面壓力分布，首先定義核心旋轉角速度:

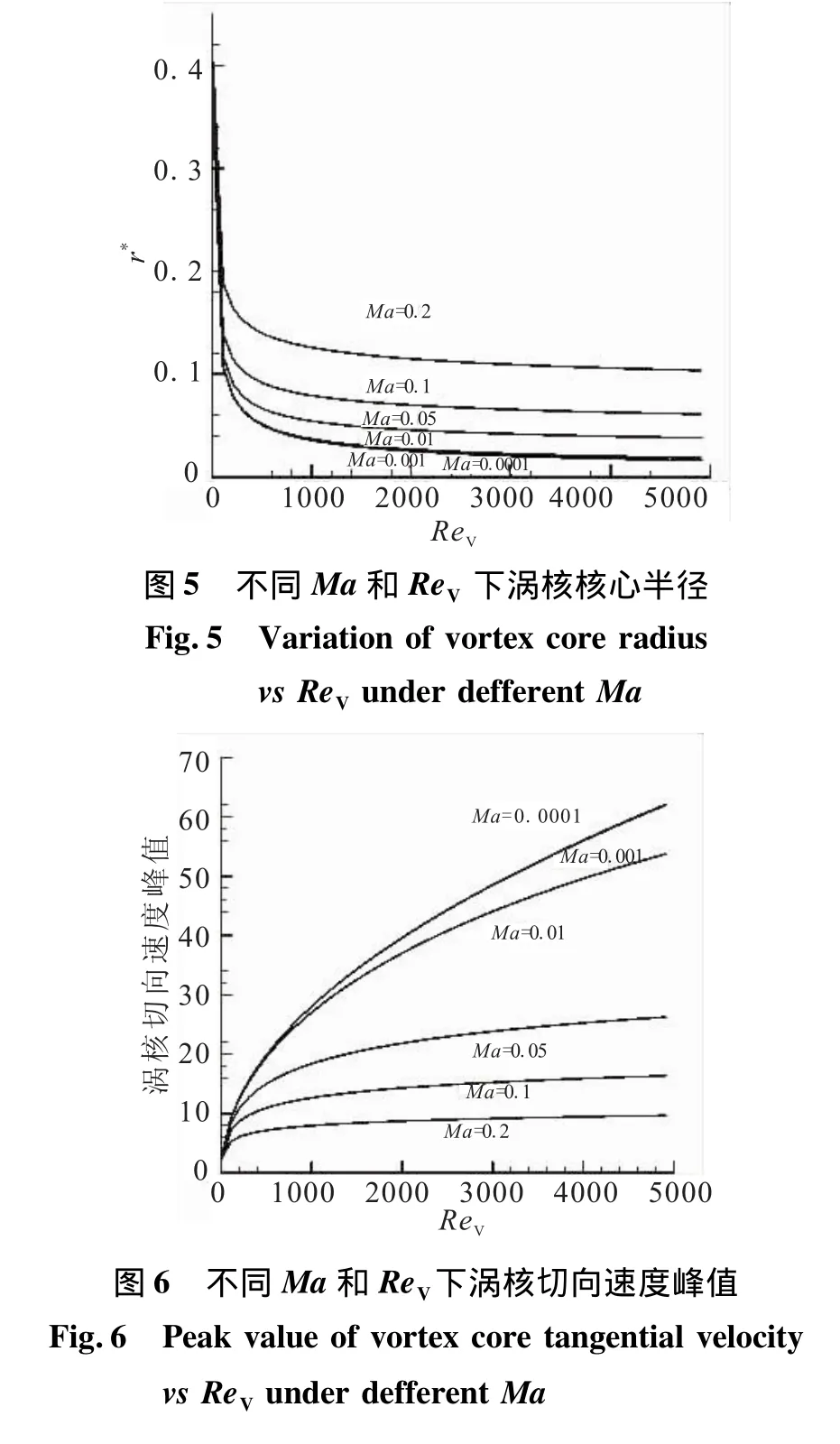
即當音速c→∞，ω*等于不可壓縮流體的結果。r*的確定同式(45)。不同馬赫數下渦核轉速ω*隨ReV的變化見圖4。

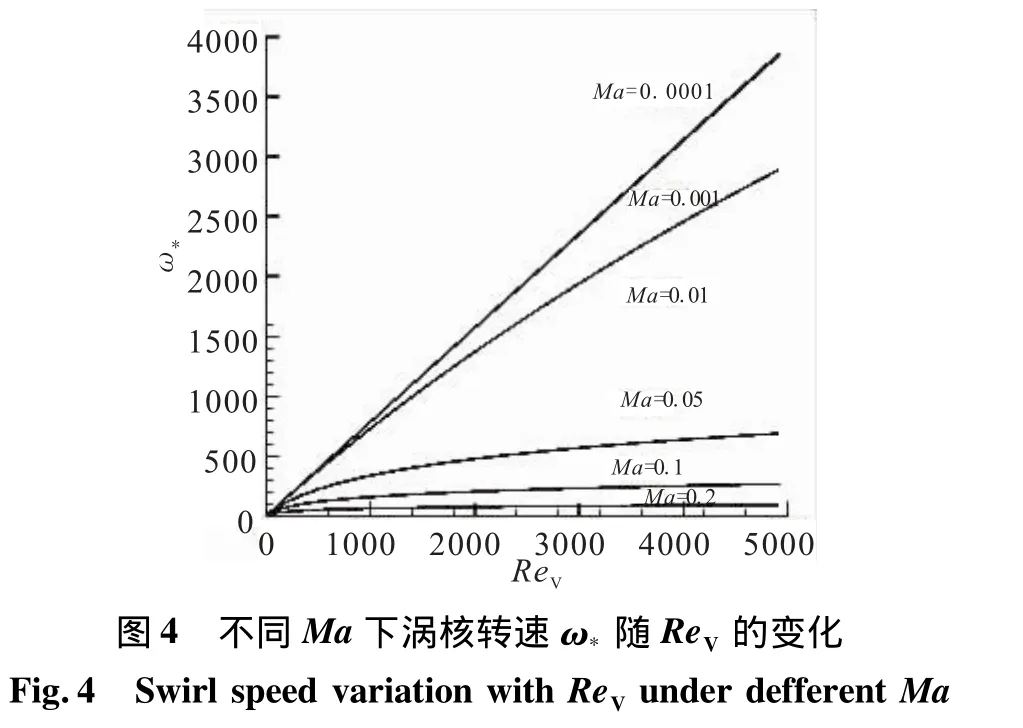
由圖4可看出，可壓縮性對渦核結構的影響較大，隨旋轉速度增大，可壓縮的影響加劇，渦核轉速對ReV的依賴程度急劇減小，并趨于平緩。而渦核半徑隨轉速的增加而增加，尤其對于較大的ReV，當ReV＜200時，渦核半徑隨ReV的增大急劇減小，見圖5。圖6為渦核切向速度峰值與ReV和旋轉馬赫數(與轉數相對應)的關系。

2.8 求解壓力和渦量

根據式(2)與式(4)，壓力梯度可表示為

積分式(51)與式(52)，且合并:

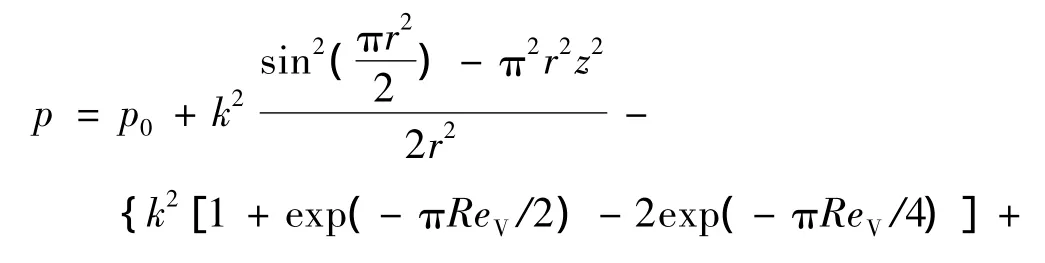
由于重新求解了切向速度，因此渦量表達式(13)也要相應地發生變化，根據式(39)與式(9)，可得到修正后的渦量表達式為

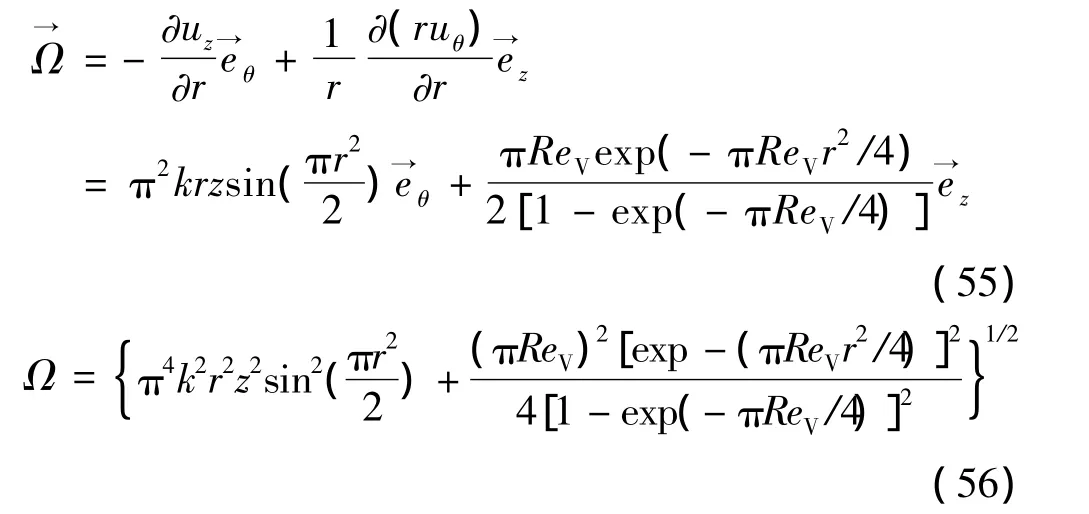
3 結論

(1)通道內不可壓縮燃氣的切向流動速度在2個區域內具有不同的特點，在小于r*的圓柱氣流核心區，切向速度呈“準固體”特征，其旋轉角速度ω*明顯超過通道旋轉角速度ω;而大于r*的區域切向流動為自由旋流。

(2)由于在旋轉角速度很高的情況下，不可壓縮的假設會帶來較大誤差，因此對高速旋轉的通道，應考慮可壓縮性的修正。可壓縮性對渦核結構的影響較大，隨著旋轉速度的增大，可壓縮的影響加劇，渦核轉速對注入雷諾數的依賴程度急劇減小，并趨于平緩。而渦核半徑隨轉速的增加而增加，尤其對于較大的ReV。

［1］Langhenry M T.Acceleration effects in solid propellant rocket motors［J］.AIAA Journal，1986，15:77-90.

［2］Mager A.Approximate solution of isentropic swirling flow through a nozzle［J］.ARS Journal，1961(8):1140-1148.

［3］Bastress E K.Interior ballistics of spinning solid propellant rockets［J］.J.Spacecraft Rockets，1965(3):12-25.

［4］Manda L J.Spin effects on rocket nozzle performance［J］.Spacecraft Rockets，1965(3):36-45.

［5］Nontan D J.An analytical and experimental investigation of swirling flow in nozzle［J］.AIAA Journal，1968(10):102-110.

［6］Dunlap R.An investigation of the swirling flow in a spinning end-burning rocket［J］.AIAA Journal，1969，7(12):2293-2299.

［7］Fuchs M D.A parametric study of the effects of acceleration on the burning rate of metalized solid propellants［J］.Journal of Spacecraft and Rockets，1982，19(6):539-544.

［8］Boraas S.Modeling slag deposition in the space shuttle solid rocket Motor［J］.Journal of Spacecraft and Rocket，1984，21(11):36-47.

［9］萊茲別格B A，葉羅欣B T，沙母索諾夫K п.固體火箭發動機系統工作過程的理論基礎［M］.劉光宇，梅其志，譯.北京:國防工業出版社，1984:369-392.

［10］邵愛民.大型固體發動機旋轉試車頭部熱防護工程分析［J］.固體火箭技術，1998，21(3):7-12.

［11］蔡國飆，田輝.旋轉對固體火箭發動機的影響［J］.推進技術，1999，20(1):11-15.

［12］高波，葉定友，侯曉.旋轉固體發動機燃燒室燃氣湍流流動數值模擬［J］.推進技術，1999，20(6):23-27.

［13］王革，陳亮，郜冶，等.旋轉對固體火箭發動機燃燒室燃氣流動的影響［J］.空氣動力學學報，2008，26(2):208-211.

［14］王革，陳亮，郜冶.旋轉管狀裝藥固體火箭發動機燃燒室流動特征［J］.彈道學報，2008，20(3):5-8.