新型寬速域高超聲速飛行器氣動特性研究①

李世斌，羅世彬，黃 偉，柳 軍，金 亮

(國防科學技術大學高超聲速沖壓發動機技術重點實驗室，長沙 410073)

0 引言

Nonweiler于1959年率先提出了乘波構型的概念［1］，引起了世界各航天科學家的興趣。進入21世紀，乘波構型飛行器的研究達到了空前的高度，關于乘波飛行器的研究逐漸進入實用化。2010年5月26日，X-51A的第一次試飛成功，加速了乘波構型的研究。乘波構型飛行器已經成為高超聲速飛行器研究的主流，也是解決高超聲速飛行難題的有效途徑之一。

國內外關于乘波體飛行器開展了大量的研究工作。陳小慶、崔凱和 Huang等［2－4］在單馬赫數條件，進行了乘波體的構型設計與性能研究，并根據不同的優化目標得到了相應的最優構型。Starkey、耿永兵和何烈堂等［5－9］分別在不同馬赫數條件下，對不同乘波體飛行器的氣動性能進行了系統研究，并考慮了不同外形在其非設計工況下的氣動性能，在乘波體構型研究中取得了豐碩的研究成果，但其設計理念的根本是針對單馬赫數條件下的特定流場，而這種針對某一特定的乘波體構型，不能夠實現寬速域均具有良好氣動特性的目標。類似這方面在單馬赫數下乘波飛行器氣動性能的研究很多，但針對以寬速域飛行器為目標的設計研究才剛起步，國內只有王發民等［10］對寬速域乘波布局飛行器進行了研究，亟急待深入探索。

以單馬赫數設計的乘波體，在非設計狀態下的氣動性能變化明顯，因而寬速域飛行器所要解決的是，乘波飛行器在更寬的速域范圍內均具有良好的氣動性能，使其在寬速域范圍內的總體性能最優。要實現此目標，不僅要考慮氣動力/熱、結構等多種學科，還要考慮各個學科之間的耦合因素。本文僅針對寬速域乘波飛行器的氣動特性進行了較深入的研究，提出了新的設計方案。

1 乘波體設計理論

在高超聲速錐形流中，氣流在激波上轉折角小于圓錐半錐角，過了激波氣流的指向還要繼續轉變，逐漸趨向于與圓錐母線平行。錐形流激波前后的流場關系可用Taylor-Maccoll方程［11］的無量綱形式表示:

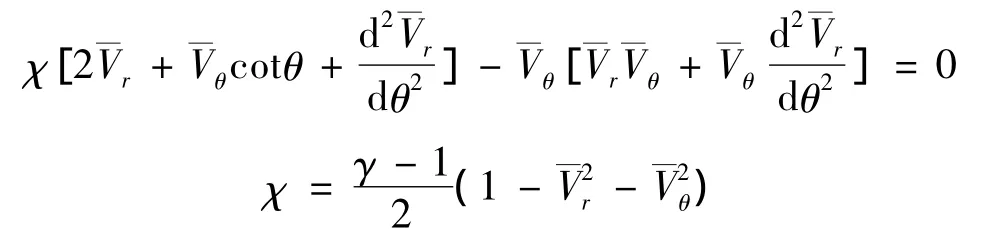
在常規乘波體生成方法中，通過數值積分以上公式，可獲得錐形流內的流線分布。本文對乘波體生成方法進行了簡化，如圖1所示。假設氣流在激波上轉折角與圓錐半錐角相同，即圓錐激波內的流線與圓錐母線平行，則可由解析方法獲得錐形流內的流線分布。

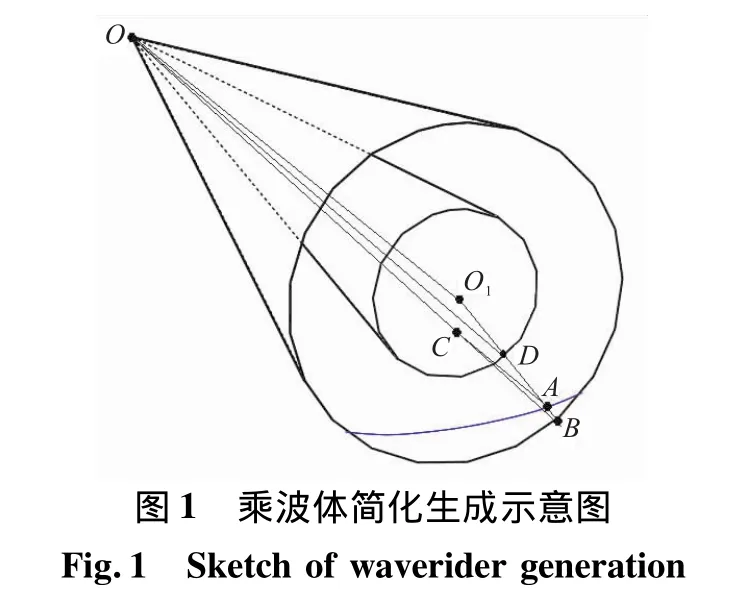
定義自由來流馬赫數、圓錐激波半錐角、圓錐底面半徑以及乘波體機身下表面的后緣曲線形狀，就可根據流線追蹤的方法獲得乘波體下表面前緣曲線，之后將前緣線向底面投影，完成整個乘波體機身的設計。

2 計算模型

由于乘波構型隨激波角的變化曲線不大［10］，在12°激波角條件下的性能較好，故本文采用的激波半錐角β=12°，圓錐底面半徑R=1 200 mm。首先分別針對Ma=4和Ma=8進行了乘波體的氣動外形設計，設計參數如表1所列，進而將兩者進行“串聯”拼接，設計了一類新型的高超聲速飛行器，如圖2所示。

表1 基準(JZ)乘波體構型的設計參數Table 1 Parameters of the benchmark waverider configuration

表1 中，a= －0.5，b=0.5，c=1;JZ-1 與 JZ-2 與圓錐底面的交點相同，圓錐底面圓心與JZ-2后緣線圓心之間的距離d=790 mm。

新型乘波構型的設計參數如表2中所列，其中L為連接段的長度，H為連接段的寬度。將JZ-1進行全尺度縮比作為其前體，并取JZ-2全長的43%作為其后體，使前體后端面和后體前端面的寬度相同，然后將其進行點對點放樣產生連接段，如圖2所示。取最大迎風面的后端面面積作為參考面積，即與JZ-2的參考面積相同。

表2 “串聯”乘波構型(CL)的設計參數Table 2 Parameters of the combined waverider

3 計算方法

采用三維隱式RANS方程和RNG k-ε湍流模型對新型寬速域高超聲速飛行器氣動性能進行數值仿真，可壓縮氣體的湍流方程可在適當的參考系下進行描述［12］。

式中 ρ、ui、p、τij、Fbi、Q、Cμ分別為密度、組分速度、壓強、湍流剪切應力、質量組分力、主體供熱和渦流粘度;Gk、YM和S分別指由速度梯度引起的湍動能量、在可壓縮湍流中膨脹-耗散提供的能量和平均應變張量系數;αk和αε分別指在k和ε方程中的普朗特數;模型常數 Clε=1.42，C2ε=1.68 可由經驗公式得到。

粘性系數和熱導率均由質量平均混合法則，采用無滑移和絕熱的壁面條件，計算域的外場條件為壓強遠場［13］。

由于幾何模型具有對稱性，故數值模擬時只需采用一半的流場來進行模擬;壁面函數采用近壁面流動模型，氣體為熱理想氣體。

收斂標準:當殘差曲線下降到10－3量級且流通量降為0.001量級時，可認為計算收斂;計算網格在機身壁面處進行加密處理;參考面積均取各模型的后端面，表3為計算模型及各模型的參考面積。

初始條件:以H=25 km、Ma=6時的狀態大氣參數為基準，pe=2 511.01 Pa、Te=221.65 K，采用等動壓設計方法，設計范圍為 Ma=4～12，動壓 p=64 240.97 Pa。

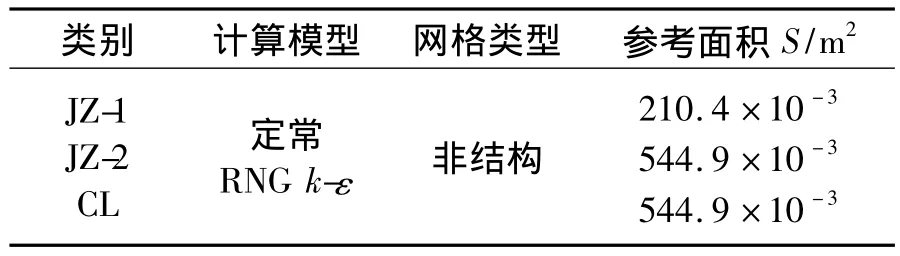
表3 計算模型及參考面積Table 3 Computational model and reference areas

采用本文的數值方法，對高超聲速細長體飛行器流場進行了數值模擬，獲得的升阻比和俯仰力矩系數結果與實驗數據吻合較好，參見文獻［12］，表明本文所采用的數值方法可用于高超聲速飛行器流場的模擬。

4 結果與分析

由升力系數和阻力系數計算公式，可得不同模型的CL、CD及升阻比L/D隨馬赫數的變化規律，如圖3所示。

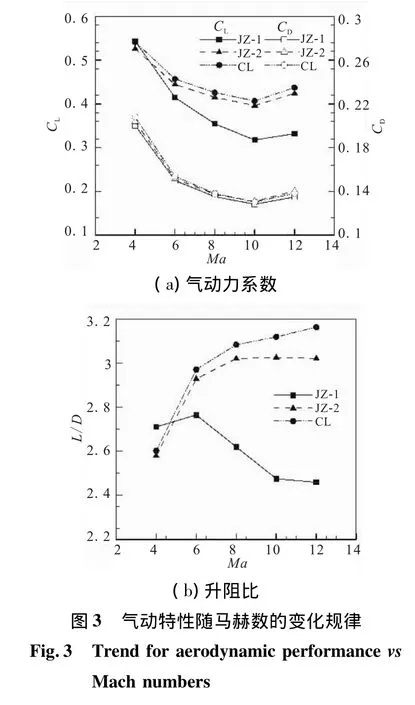
由圖3(a)可知，隨著馬赫數增加，基準模型和“串聯”模型的氣動力系數先急劇降低后增加;JZ-1的升力系數降低幅度較大，“串聯”乘波體的升力系數高于基準乘波體;而“串聯”模型的阻力系數和基準模型的阻力系數幾乎保持一致;說明連接段使“串聯”乘波體的升力系數特性改進，進而提高其升阻比，改善其氣動性能。

由圖3(b)可知，JZ-1的升阻比先增加后降低，馬赫數在6～10時升阻比呈線性急劇降低，JZ-1的氣動性能隨馬赫數的變化較大，說明外形太薄的飛行器氣動性能不穩定;JZ-2的升阻比隨馬赫數的增加先升高后幾乎保持不變，“串聯”乘波體的升阻比隨馬赫數的增加不斷升高;當Ma＞8時，“串聯”乘波體的升阻比變化不明顯。在Ma=4時，“串聯”乘波體的升阻比高于JZ-2卻低于JZ-1，而在高馬赫數下，其升阻比始終高于其他模型，說明“串聯”組合乘波飛行器的氣動性能，在合適的飛行馬赫數條件下能夠使氣動性能達到最優。在設計范圍內，“串聯”乘波體的升阻比最大接近3.2，高于基準模型;而目標Ma=6時，并不能取得最大的升阻比，“串聯”乘波體的升阻比接近3.0;“串聯”乘波體的升阻比隨馬赫數增加而變大，而JZ-1的升阻比在Ma＞6的情況下，隨馬赫數升高而降低，說明JZ-1乘波體對新型寬速域乘波體的影響不明顯，JZ-2乘波體在整體氣動性能中起主要作用;連接段改善了“串聯”乘波體的性能，說明兩者適當的組合可達到“串聯1+1＞2”的效果。

圖4所示為Ma=8、0°攻角飛行狀態下的等值線分布云圖。高壓區主要集中在下表面，乘波特性較好。從圖4可見，由于錐導乘波的設計是根據無粘流場特性生成的，故在乘波體邊緣存在部分高壓向上表面溢流的現象。

圖5所示為Ma=8、0°攻角飛行狀態下，對稱面上連接段處靜壓的等值線圖。

結合圖4和圖5可知，高壓區幾乎全部在機體的下表面，連接段適當的坡度可提高“串聯”乘波體的升力特性;而在連接段上表面處存在一定的壓強，這將導致阻力的增加，適當的改善連接段的外形將能夠降低乘波體飛行器的阻力性能，改善乘波體的整體氣動性能。

在設計目標Ma=6下，數值模擬了攻角對氣動特性的影響，圖6為氣動特性隨攻角的變化規律。

由圖6(a)可知，升力系數隨攻角的增加成線性增加，阻力系數隨攻角的增加而增大，且增大幅度越來越大;JZ-1的升力系數和阻力系數增加更快，“串聯”乘波體的氣動力系數隨攻角變化趨勢與JZ-2基本一致。由圖6(b)可知，升阻比隨攻角先增加后降低，“串聯”乘波體和JZ-2升阻比的變化趨勢相似，在3°攻角時升阻比達到最大;JZ-1的最大升阻比達到4.714，“串聯”乘波體的升阻比在3°攻角條件下達到3.48，而且其升阻比在正攻角條件下始終處于JZ-1和JZ-2之間;在正攻角飛行狀態下，JZ-1的升阻比明顯高于JZ-2的升阻比，故JZ-1可作為“串聯”乘波體的一部分來提高其升阻比。

由文獻［14］可知，當 ?Mz/?α ＜0時，飛行器具有縱向靜穩定性。由圖6(c)可知，在－2°～10°攻角范圍內，俯仰力矩系數隨攻角增加單調遞減，故而飛行器具有靜穩定性，這是由于CM的參考點位于飛行器的50%處，使壓心位于質心之后的緣故，使飛行器產生低頭力矩。

5 結論

(1)“串聯”方式的新型乘波飛行器的氣動性能在寬速域范圍內比單馬赫數條件下的乘波飛行器的氣動性能更優;選擇合適的連接段可使飛行器的氣動性能較優，達到“串聯1+1＞2”的效果。

(2)“串聯”乘波體的升阻比隨馬赫數的增加而變大，當Ma＞8時，其氣動特性變化不明顯，最大升阻比接近3.2，在設計馬赫數范圍內，升阻比不低于2.6。

(3)“串聯”乘波體的升阻比隨攻角的增加先增加后減小，在3°攻角時升阻比最大。在Ma=6下，JZ-1的最大升阻比為4.714，“串聯”乘波體的最大升阻比達到3.48;在正攻角飛行狀態下，JZ-1的升阻比明顯高于JZ-2，故可作為“串聯”乘波體的一部分用來提高其氣動特性。

［1］Nonweiler T R F.Aerodynamic problems of manned space vehicles［J］.Journal of the Royal Aeronautical Society，1959，63:521-528.

［2］Huang Wei，Ma Lin，Wang Zhen-guo，et al.A parametric study on the aerodynamic characteristics of a hypersonic waverider vehicle［J］.Acta Astronautica，2011，69:135-140.

［3］陳小慶.高速乘波飛行器氣動布局設計研究［D］.長沙:國防科技大學，2006.

［4］崔凱，楊國偉.6馬赫錐體流場對乘波體性能的影響及規律［J］.科學通報，2006，51(24):2830-2837.

［5］Mazhul I I，D R R.Hypersonic power-law shaped waveriders in off-design regimes［J］.Journal of Aircraft，2004，41(4):839-845.

［6］Starkey R P，J LM.Analytical off-design lift-to-drag-ratio analysis for hypersonic waveriders［J］.Journal of Spacecraft and Rockets，2000，37(5):684-692.

［7］耿永兵，劉宏，姚文秀，等.錐形流乘波體優化設計研究［J］.航空學報，2006，27(1):23-29.

［8］何烈堂，周伯昭，陳磊.基于乘波構型的跨大氣層飛行器氣動布局［J］.國防科技大學學報，2007，29(4):17-21.

［9］劉濟民，侯志強，宋貴寶，等.前緣鈍化對乘波體非設計點性能影響分析［J］.飛行力學，2011，29(1):21-25.

［10］王發民，丁海河，雷麥芳.乘波布局飛行器寬速域氣動特性與研究［J］.中國科學 E輯:技術科學，2009，39(11):1828-1835.

［11］左克羅，霍夫曼(美).氣體動力學［M］:國防工業出版社，1989.

［12］Huang Wei，Li Shi-Bin，Liu Jun，Wang Zhen-Guo.Investigation on high angle of attack characteristics of hypersonic space vehicle［J］.Science China Technological Sciences，2012，55(5):1437-1442.

［13］李世斌，羅世彬，黃偉，等.新型高超聲速飛行器氣動構型設計［J］.彈箭與制導學報，2012(錄用待刊).

［14］黃偉，柳軍，羅世彬，等.尾噴管構型對高超音速飛行器縱向靜穩定性的影響［J］.固體火箭技術，2008，31(4):310-312.