計及互感的開關磁阻電機單雙相勵磁靜態性能分析

高潔， 孫鶴旭， 米彥青， 董硯， 何林

(1．河北工業大學控制科學與工程學院，天津 300130;2．天津清源電動車輛有限責任公司，天津 300450;3．天津職業技術師范大學自動化與電氣工程學院，天津 300222)

0 引言

開關磁阻(switched reluctance，SR)電機的結構和工作原理比較簡單，但其特有的雙凸極結構定轉子齒交疊前產生的邊緣磁通引起電流非線性變化;并且開關電源供電使得轉矩是由一系列脈沖轉矩疊加而成，合成轉矩亦非恒定值。這導致SR電機存在固有的轉矩脈動，尤其電機低速運行時轉矩脈動較大［1］，轉矩脈動抑制的研究是近年來SR電機研究領域的熱點之一，國內外學者從電機結構、電流優化控制等方面做了大量卓有成效的工作［2－3］。

為了減小轉矩脈動，保持各相導通時電感曲線相互重疊是研究者所期望的，因而各相間的交互是不可避免的，一般SR電機的各相磁鏈和轉矩分別計算，且通常忽略互感［1］。各相間的交互可歸為兩類:互感耦合及飽和效應。其中互感耦合是由于各相磁鏈交鏈引起的，而互感飽和則是下一相勵磁時對前一導通相在其飽和區所產生的影響，飽和進而影響了磁鏈和輸出轉矩。通常情況下，SR電機的設計準則之一就是互感盡可能小，可以使得各相單獨控制。然而大多數SR電機即使單相勵磁時也工作在磁飽和區域，此時本身互感效應就已不能忽略，且下一相勵磁過程中與前一相交鏈的磁路部分也將影響其飽和程度。

已有的文獻［4－7］通常只是考慮了互感耦合效應，而往往忽略了互感的飽和。本文從電機設計的角度分析互感飽和的影響，利用有限元法詳細分析相鄰相對導通相磁鏈的影響，以及互感對輸出轉矩的影響。隨著相數的增加，SR電機運行時的重疊區域也變得更大，由于四相8/6結構磁路的非對稱性，本文將對此結構重點分析。

1 SR電機互感耦合分析

1.1 SR電機單相勵磁模式互感耦合分析

互感的一般定義式為

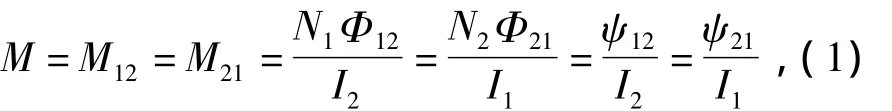
式中:N1、N2分別是線圈 1、2 的匝數;Φ12和 ψ12分別是線圈2中的電流I2在線圈1中產生的每匝磁通量和磁鏈，Φ21和ψ21分別是線圈1中的電流I1在線圈2中產生的每匝磁通量和磁鏈。

互感系數的大小取決于兩個線圈的幾何形狀，大小，相對位置，各自的匝數以及它們周圍介質的磁導率。在SR電機中，各相繞組的幾何形狀、大小、相對位置及匝數都是固定的。但是線圈之間是通過轉子耦合的，當轉子轉動時各相線圈間的磁阻發生著周期性的變化，此周期和轉子的極數相關。

下面對SR電機單相勵磁情況進行有限元分析，各相依次通入7 A的方波電流，每相導通15°，通電周期為一個轉子極距60°，SR電機繞組采用NSNSSNSN排列方式，其自感和互感曲線如圖1所示，AB、BC、CD相鄰相均為短磁路連接，極性相反，導通相磁力線與其相鄰相的磁場方向一致，互感磁鏈具有加強相鄰相磁場的作用，因此其互感均為正值;而DA相為長磁路連接，兩相極性相同，導通相A的磁力線與相鄰相D的磁場方向相反，互感磁鏈則會減弱D相的磁鏈，因此互感為負。

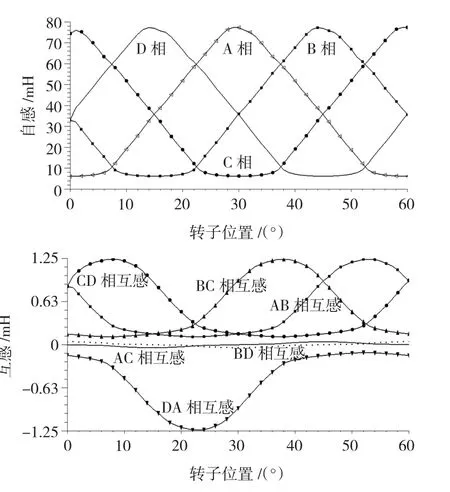
圖1 NSNSSNSN連接方式時單相勵磁各相自感和互感特性曲線Fig．1 The self and mutual inductance of single phase excitation with NSNSSNSN connection

同樣地，如圖2所示，SR電機為NNNNSSSS時，AB、BC、CD相鄰相均為長磁路連接，其互感均為負值，而DA兩相為短磁路連接，其互感值則為正。且對齊位置自感值近似為非對齊位置的12.5倍，這就為控制相電流和磁鏈帶來了難度。相鄰相的互感不超過與之相關自感值的6.4%，而非相鄰相的互感則不超過0.07%，因此，盡管在文獻［8］中非相鄰相的互感用于在無位置控制中檢測轉子位置，但是其他情況下該互感基本可以忽略。

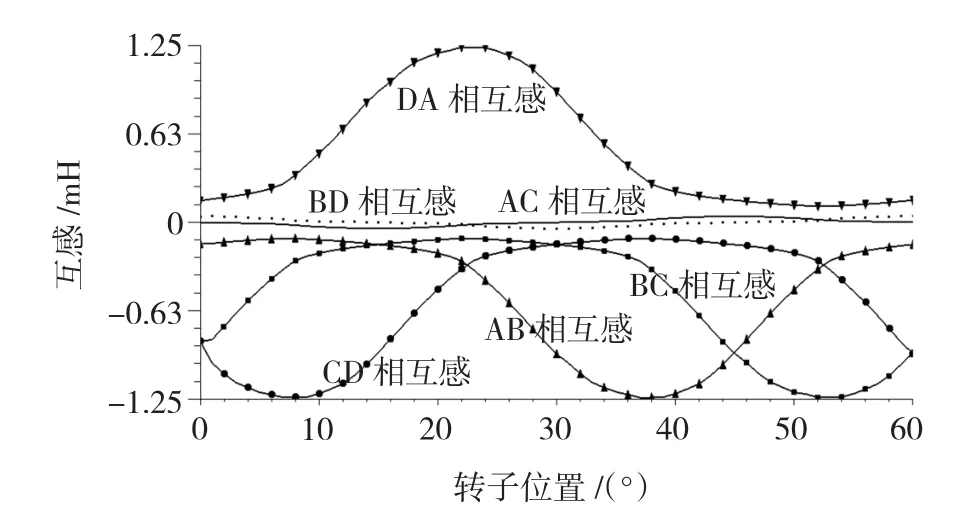
圖2 NNNNSSSS連接時單相勵磁各相自感和互感特性曲線Fig．2 The self and mutual inductance of single phase excitation with NNNNSSSS connection

1.2 SR電機雙相勵磁模式互感耦合分析

與SR電機單相勵磁類似，兩相同時導通的互感也不僅僅是各自單相導通的線性疊加，如圖3所示。對各相依次通入7A方波電流，每相導通30°，通電周期亦為60°。兩相同時勵磁對于減小轉矩脈動和降低相電流都是有利的，但是互感耦合不可忽略。這也是高性能SR電機控制研究互感耦合效應的重要性。

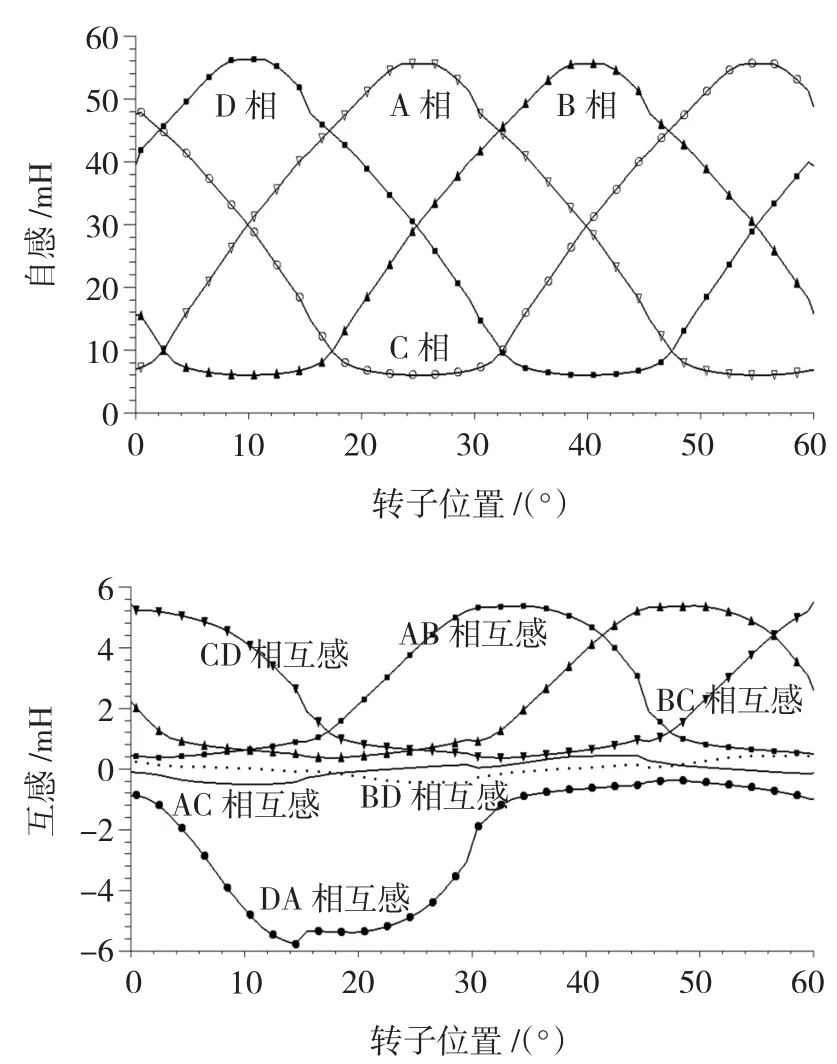
圖3 NSNSSNSN連接方式時兩相勵磁自感和互感特性曲線Fig．3 The self and mutual inductance of double phase excitation with NSNSSNSN connection

進一步對兩相勵磁模式不同電流下長、短磁路的自感和互感進行分析，如圖4所示，DA相長磁路勵磁互感均為負值，這是由于DA相間的磁路較長，而軛部的磁飽和使得DA間的互感磁鏈沿不飽和的DA相間的軛部穿過兩相線圈。在短磁路模式下，當勵磁電流較大時，由于磁飽和的原因使得DA相間較短軛部的磁阻增大，互感磁鏈沿著較長但是磁阻較小的軛部穿過DA相，所以互感也為負值。當電流較小時，短軛部的磁阻小于長軛部，互感磁鏈會先擇較小的短軛部磁路閉合，所以此時互感值為正。

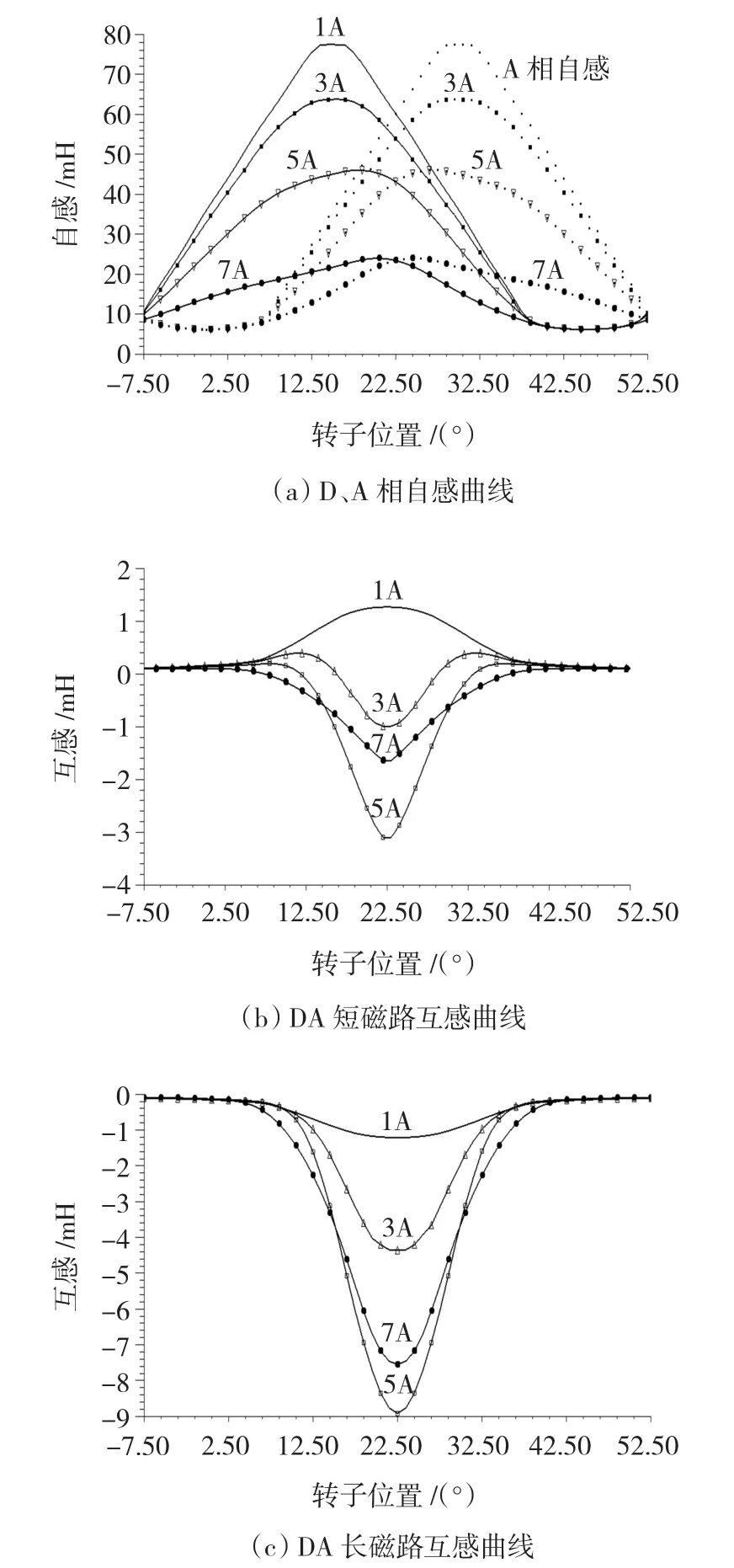
圖4 兩相勵磁模式下不同電流對應的自感與互感曲線Fig．4 The self and mutual inductance of double phase excitation corresponding to different currents

同時從圖4可知，在相同的轉子位置和較大的勵磁電流情況下，長磁路互感的絕對值比短磁路要大，這是由于在長磁路模式下互感磁鏈閉合路徑的磁阻要小于短磁路模式。而電流較小時，兩個互感磁鏈閉合路徑的磁阻相差不大，所以互感絕對值相差不大。

從圖4中還可以看出，當轉子轉到22.5°時，即DA兩相和轉子極的重合面積相等時，DA相間互感達到最大，相間磁阻最小。當轉子轉到－7.5°或52.5°位置時，即轉子極和DA相間的定子槽對齊位置時，DA兩相和轉子均無重合，此時DA相間磁阻最大，互感達到最小值，兩互感曲線關于22.5°位置軸對稱。

2 SR電機互感飽和分析

2.1 SR電機單雙相勵磁磁力線分布

相繞組間互感的飽和效應，其機理與自感相同，只是主要考慮兩相繞組互感磁路飽和度的變化，而不是某一相繞組磁路。首先，定義定轉子齒槽對齊位置為0°，定轉子齒齒對齊位置為30°，電機逆時針轉動，A相為導通相，D相為其前置相，B相為滯后相，四相8/6極SR電機導通角為15°，單相導通時如圖5(a)中。若導通角小于15°，相電流不會相互重合，但是為了減小轉矩脈動，通常使得相鄰相電流要有一定的重疊區域，如圖5(b)所示為DA兩相長磁路模式，除了兩相間定子軛部磁鏈方向相反外，其余定子軛部的磁鏈方向都相同。即使只有一相導通，定子軛部在某個轉子位置時也有部分飽和，特別是位于對齊位置處。類似地，圖5(c)為DA兩相短磁路模式，除了DA兩相間定子軛部磁鏈方向相同外，其余定子軛部磁鏈方向都相反，也即其余部分的磁阻減小。

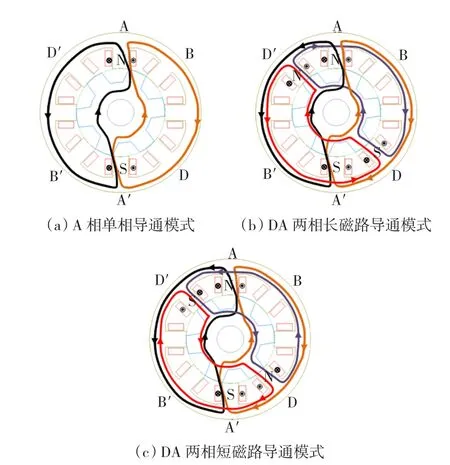
圖5 導通相磁路曲線Fig．5 Leading phase influence on flux

圖6(a)所示為A相勵磁的磁場分布圖，轉子位置角為15°，單相勵磁時，定子軛部的磁力線被對稱均分，其磁密近似相等。圖6(b)所示為DA兩相長磁路模式導通，此時D相處于齒齒對齊位置，A相仍處于15°位置，此時相當于勵磁電流關斷位置。由于兩相繞組同時勵磁時，相間磁場相互耦合，定轉子軛部磁通量大幅增加，磁場的飽和程度和分布情況也與單相勵磁磁場有較大區別。圖6(c)所示為DA兩相在短磁路模式導通的磁場分布圖，DA兩相之間的定子軛部磁場高度飽和。因此為了減小飽和效應和降低銅耗，SR電機應采用短磁路連接，同時亦可以增大輸出轉矩。

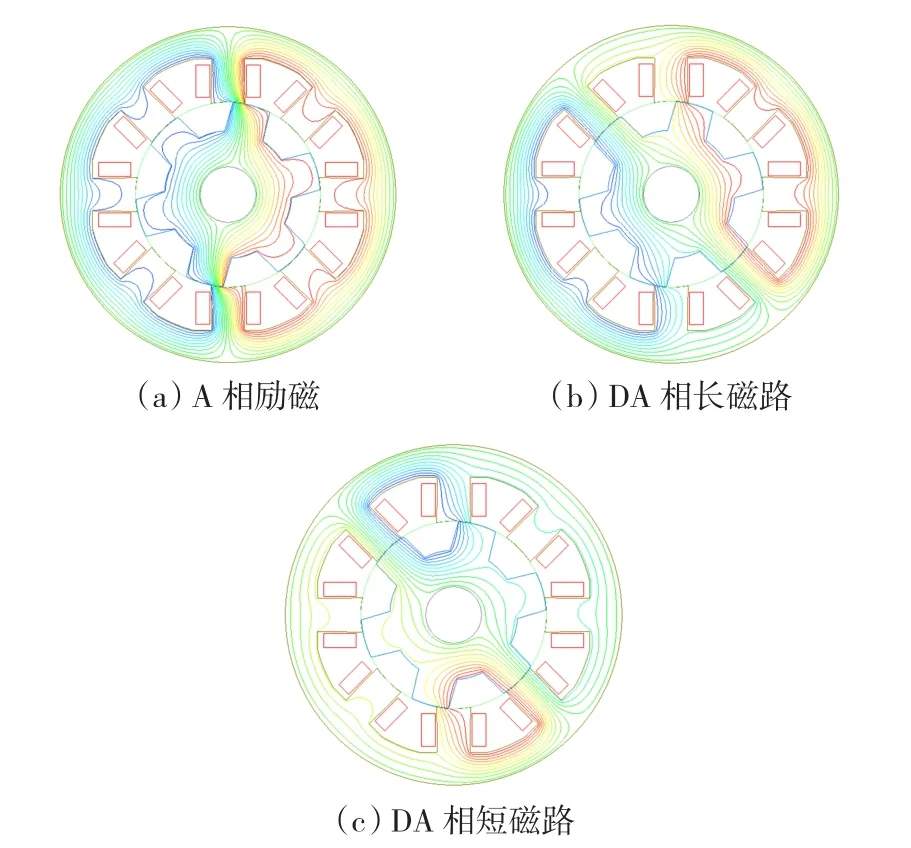
圖6 導通相磁力線有限元分析圖Fig．6 Finite-element plots of flux lines for the excitation phases

由圖5、圖6可知，當SR電機單相勵磁處于齒槽對齊位置時，氣隙磁阻較大，漏磁通也較大。當定轉子極部分重合時，其極身的局部飽和最為嚴重。隨著重合面積增大，定、轉子極身的局部飽和度將逐漸減小，完全重合時，除極尖部分外，其它部分基本上不飽和。DA兩相勵磁和單相勵磁的磁場分布及飽和程度均有較大差別，主要體現在軛部磁路上。以D相為例，單相勵磁時定轉子軛部磁通約為齒部的一半，而DA兩相同時勵磁時，定轉子軛部和齒部磁通基本相等。因此兩相勵磁時軛部磁勢降因磁路過飽和而大幅增加，將導致每相磁通減小，從而每相磁鏈減小。

2.2 SR電機兩相勵磁模式互感飽和分析

下面分析兩相勵磁時互感飽和的影響，對于導通相A而言，同時給D相或B相輸入恒定等值電流計算磁鏈。如圖7所示，實線為A相在0～30°范圍內勵磁磁鏈曲線;左箭頭虛線表示DA兩相在0～15°范圍內同時勵磁的A相磁鏈曲線，即兩相長磁路連接方式;下三角虛線代表AB兩相在15～30°范圍內同時勵磁的A相磁鏈曲線，也即短磁路連接方式。由圖7可知，相電流在0到2 A范圍內，磁場尚未飽和，磁鏈與勵磁電流為線性關系，磁鏈線性疊加，3種勵磁方式下的磁鏈特性基本重疊;當相電流大于2 A時，磁場開始飽和，且單相勵磁時定轉子軛部磁通密度比兩相勵磁小，飽和程度低，磁勢降亦小，因此相電流相同時磁鏈相對較大;而兩相勵磁時，長磁路勵磁模式下定、轉子軛部路徑長度分別是短磁路勵磁方式的3倍和2倍，軛部具有更大的磁勢降;所以長磁路勵磁模式各相磁鏈最小，短磁路次之，單相勵磁時最大。

進一步分析不同轉子位置的磁鏈變化:首先從非對齊位置到15°之前范圍內分析，當A相位于定轉子齒槽對齊位置時，單相導通的磁鏈值最小;在此區間內，D相定、轉子還未到達齒齒對齊位置，因而其磁鏈未達到峰值，且D相若是處于非對齊位置區間內，其對A相的影響很小。然而，當A相處于15°時，由于定轉子極重合面積增大，其自身磁鏈值增大，此時D相處于齒齒對齊位置，磁鏈達到峰值，互感飽和也在此點增強。轉子處于15°位置時，B相開始導通且處于齒槽對齊位置，而D相處于齒齒對齊且勵磁電流關斷狀態。當轉子逐漸轉至30°，A相處于齒齒對齊位置，此時，定子軛部的磁鏈將由D相對其影響較大狀態過渡到B相的影響較小狀態，圖7同時也表明了轉子轉到15°時磁鏈產生躍變，這是因為此位置D相處于完全對齊并且磁鏈最大，接著D相關斷，B相開始導通，此時B相處于非對齊位置且磁鏈最小，與D相相比，B相在15°的影響可以忽略。B相對A相磁鏈的影響隨著其達到齒齒對齊位置而增強，兩相磁鏈同時增加，此時已不可忽略。

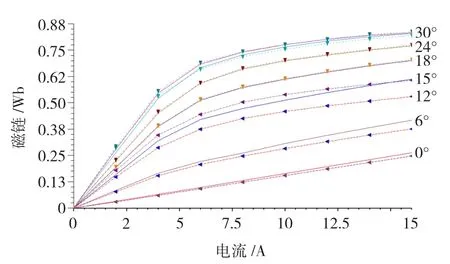
圖7 單雙相勵磁磁鏈曲線Fig．7 The flux lines of both single and double phase excitation

因此當SR電機處于兩相勵磁模式時，若采用單相勵磁獲取的磁鏈計算電機的磁共能進而求得輸出轉矩，將產生較大誤差，尤其當相鄰兩相為長磁路勵磁模式時。為準確地反映兩相勵磁時由于相間耦合、磁場分布以及飽和導致的磁鏈與單相勵磁的差別，必須考慮互感飽和及耦合的影響。

3 SR電機互感特性的實驗研究

為了驗證上述模型的正確性，本文利用數字電橋來測量各相的電感值和各相間的互感值。常用的互感的測量方法有:磁通法、伏安法、串聯法等［9－10］。本文采用的串聯法，這種方法電路連接簡單，讀數方便。

兩個具有互感的線圈若是異名端相連則為順向串聯，若是同名端相連則為反向串聯。順向串聯有

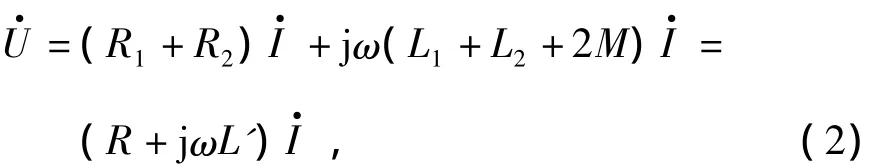
式中:R為兩線圈的等效電阻;L為順向串聯的等效電感，且有L=［(U/I)2－R2］0.5/ω。

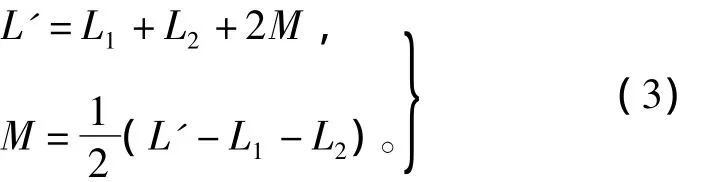
反向串聯有

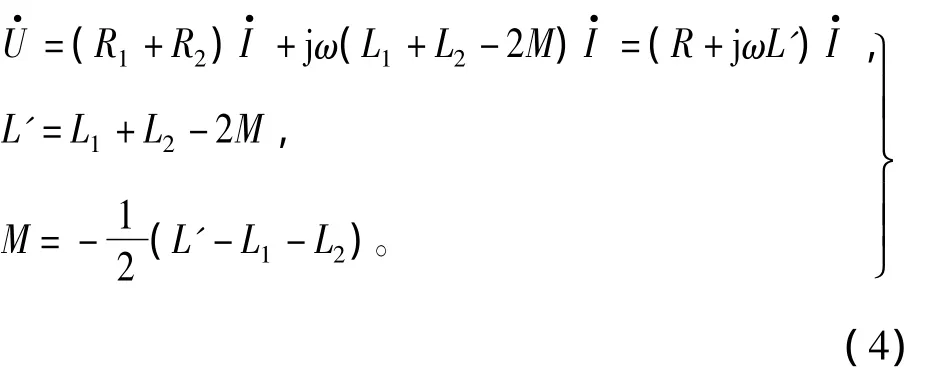
對四相8/6結構的SR電機進行測試，測量時DA兩相是順向串聯，其它相均為反向串聯。測試時讓電機軸的中心和萬能分度頭的軸心處于同一個水平位置。使萬能分度頭帶動電機軸轉動，萬能分度頭的蝸輪、蝸桿的減速率為40∶1，而分度盤最外圈的孔數為66個，所以手柄每轉過一個孔，電機轉動0.136°。實驗中萬能分度頭的手柄每轉過10個孔，即電機軸每轉過1.36°則測一次電機四相，及兩兩串聯的電感。測量電感的儀器采用的是同惠電子有限公司的TH2817A數字電橋，測試環境為數字電橋輸出2 V、5 kHz的交流信號，先測量每一相的自感，再測兩相串聯的等效電感，再利用式(3)和式(4)計算出互感M，圖8為被測樣機 A、B、C、D 四相的自感曲線，以及 AB、AC、DA相間互感曲線，實驗結果與有限元分析結果趨勢一致，稍有誤差。

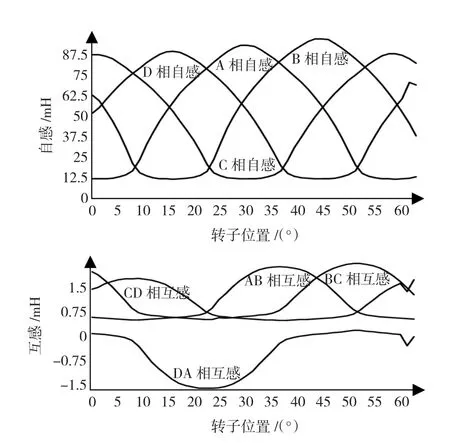
圖8 SR電機單相勵磁實測自感和互感曲線Fig．8 The self and mutual inductance test results with single phase excitation

4 SR電機互感及其對矩角特性的影響

為定性分析互感對矩角特性的影響，假設任意相鄰兩相繞組導通時，其余相電流為零且磁通為零;并有每相漏磁通為零［11－12］。利用有限元計算 SR電機分別在D相勵磁，A相勵磁，DA兩相短磁路勵磁以及長磁路勵磁方式下，如圖2所示位置的矩角特性，計算結果如圖9所示，其中TA代表A相單相勵磁轉矩，TD代表D相單相勵磁轉矩，TADS為相鄰兩相短磁路勵磁模式下的總轉矩;TADL為長磁路勵磁方式下的總轉矩，Tsum代表D、A兩相分別單相勵磁時轉矩的代數和。

圖9(a)是DA兩相繞組電流均為1 A時的矩角特性，對比DA兩相短磁路勵磁、長磁路勵磁時的輸出轉矩和分別單相勵磁時的轉矩和，可以看出三條曲線非常接近，但略有差別。這是由于勵磁電流為1 A時，磁場不飽和，磁場強度大小與勵磁電流尚為線性關系。由于勵磁電流為1 A時，短磁路互感為正，而長磁路互感為負，短磁路時輸出轉矩略大，分別單相勵磁時的轉矩和次之，長磁路最小。圖9(b)、(c)、(d)分別是 DA 相繞組電流為 3 A、5 A、7 A時的矩角特性。

轉子位置在0～8°區間內，長、短磁路的互感值都很小，繞組電流一定時，長、短磁路的磁共能與分別單相勵磁時兩相的代數和基本相等，因此DA兩相短磁路、長磁路勵磁時的矩角特性曲線以及分別單相勵磁時的轉矩之和曲線基本重疊。

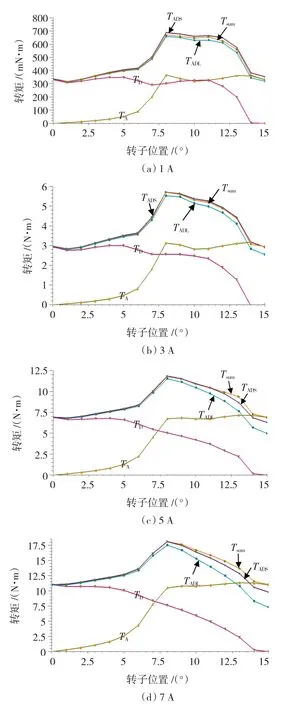
圖9 SR電機不同勵磁模式下的靜態轉矩對比曲線Fig．9 The contrast curves of the static torque for different excitation modes

轉子位置在8～15°區間內，隨著角度的增加，三條曲線的差別也越來越大。這是由于轉子位置越靠近15°，長、短磁路互感的絕對值越大，不同勵磁模式磁共能變化量的差別就越大，轉矩差別也就越大。圖9表明繞組電流較大時，長、短磁路勵磁模式下的互感均為負，且長磁路負互感的絕對值大于短磁路負互感的絕對值。兩相分別單相勵磁時的轉矩之和最大，短磁路時的輸出轉矩次之，長磁路最小。因此，有限元計算結果與理論分析結果相一致。

為了對結論進行進一步驗證，本文實測了SR樣機在額定電流下長、短磁路的轉矩，如圖10所示。理論分析和有限元計算以及實驗結果均表明，相鄰兩相為短磁路勵磁模式時，可獲取較高平均轉矩。

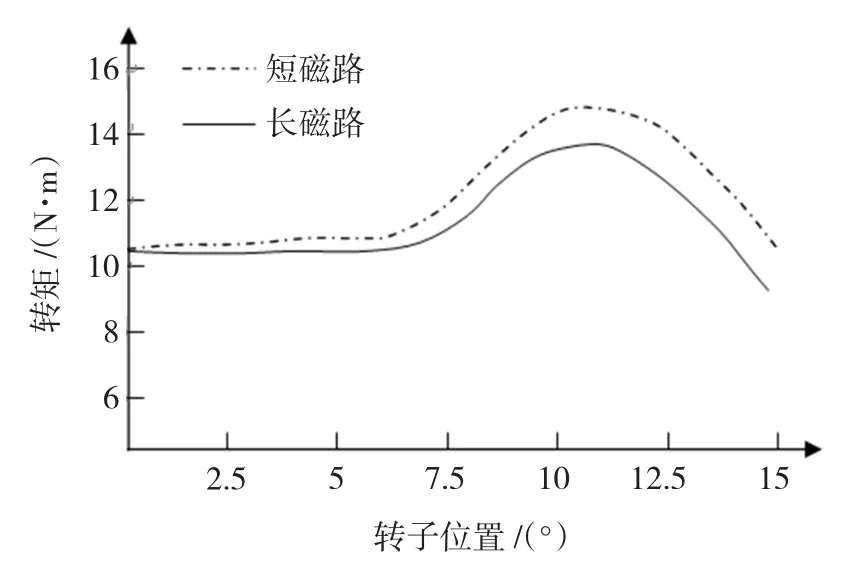
圖10 SR電機長短磁路實測轉矩曲線(i=7 A)Fig．10 The curves of the static torque for different magnetic circuits(i=7 A)

5 結語

本文以四相8/6結構SR電機為研究對象，用有限元法詳細分析了SR電機長、短磁路模式下單雙相勵磁的靜態性能。包括自感和互感曲線隨相電流及轉子位置的變化規律，并通過實驗方法進行了驗證與計算，得出當SR電機兩相勵磁模式時，若采用單相勵磁獲取的磁鏈計算電機磁共能求得輸出轉矩，將產生較大誤差，尤其當相鄰兩相為長磁路勵磁模式時。同時分析了相鄰相對導通相磁鏈的影響，以及長、短磁路模式下一個步進角內的平均轉矩，且短磁路模式下能夠獲得更高的平均轉矩。本文分析表明:為準確反映兩相勵磁時由于相間耦合、磁場分布以及飽和導致的磁鏈與單相勵磁的差別，必須考慮互感飽和及耦合的影響，為SR電機數學建模及其高性能控制提供了依據。

［1］MILLER T J E．Switched Reluctance Motors and Their Control［M］．Oxford:Clarendon，1993:7－24．

［2］LI G J，OJEDA J，HLIOUI S，et al．Modification in rotor pole geometry of mutually coupled switched reluctance machine for torque ripple mitigating ［J］．IEEE Transactions on Magnetics，2012，48(6):2025 －2034．

［3］張慧英，汪旭東，高彩霞．減小開關磁阻電機轉矩脈動、噪聲和振動方法研究綜述［J］．微電機，2009，42(8):65－68．

ZHANG Huiying，WANG Xudong，GAO Caixia．Study of optimization design methods of switched reluctance motor［J］．Micromotor，2009，42(8):65 －68．

［4］PRESTON M A，LYONS J P．A switched reluctance motor model with mutual coupling and multi-phase excitation［J］．IEEE Transactions on Magnetics，1991，27(6):5423 －5425．

［5］MICHAELIDES A M，POLLOCK C．Modeling and design of switched reluctance motors with two phase simultaneously excited［J］IEE Proceedings-Electric Power Applications，1996，143(5):361－370．

［6］PILLAY P，LIU Y，CAI W，et al．Multiphase operation of switched reluctance motor drives［C］//Thirty-Second IAS Annual Meeting-Industry Applications Conference，October 5 － 9，1997，New Orleans，USA．1997，1:310 －317．

［7］JAINA K，MOHAN N．Dynamic modeling，experimental characterization，and verification for SRM operation with simultaneous two-phase excitation［J］．IEEE Transactions on Industrial electronics，2006，53(4):1238 －1249．

［8］PANDA D，RAMANARAYANAN V．Mutual coupling and its effect on steady-state performance and position estimation of even and odd number phase switched reluctance motor drive［J］．IEEE Transactions on Magnetics，2007，43(8):3445 －3456．

［9］RADIMOV N，BEN-HAIL N，RABINOVICI R．Inductance measurements in switched reluctance machines［J］．IEEE Transactions on Magnetics，2005，41(4):1296 －1299．

［10］ZHANG Peng，CASSANI P A，WILLIAMSON S S．An accurate inductance profile measurement technique for switched reluctance machines［J］．IEEE Transactions on Industrial Electronics，2010，57(9):2972 －2979．

［11］曲兵妮，宋建成．開關磁阻電動機互感特性及其對轉矩的影響［J］．電機與控制學報，2009，13(3):332 －336．

QU Bingni，SONG Jiancheng．Mutual inductance of switched reluctance motor and its effect on torque［J］．Electric Machine and Control，2009，13(3):332 －336．

［12］LIU YAGUANG，PILLAY P．Improved Torque performance of switched reluctance machines by reducing the mutual saturation effect［J］．IEEE Transactions on Energy Conversion，2004，19(2):251－257．