用于旋轉調制捷聯慣導系統的旋轉控制方法

劉芳， 王瑋， 張仲毅

(北京航空航天大學儀器科學與光電工程學院，北京 100191)

0 引言

20世紀70年代至今，旋轉調制式捷聯慣導技術得到諸多應用和發展。國外方面包括Delco公司的代表產品“輪盤木馬”400［1］(C －400)，Litton 公司研制的低成本高精度的激光捷聯慣導系統LN－94［2］，以及英國 MARLIN 開發項目下的 MK49［3］;國內方面包括北京理工大學對旋轉調制式光纖陀螺捷聯慣導系統的誤差特性進行的仿真研究［4］，以及國防科技大學研制的用于長航時的高精度激光陀螺單軸旋轉慣性導航系統［5］。可以說旋轉調制式捷聯慣導技術受到越來越多的重視，該技術利用原有的慣性器件卻可以大幅度提高系統的導航精度［6］。與旋轉調制式捷聯慣導技術相匹配的旋轉控制技術目前已發展出了連續單方向旋轉、連續正反轉和轉位置這三種方式，其中的連續正反轉從旋轉調制的效果上講較另外兩種方式更具有優勢，主要體現在刻度系數誤差不積累，避免使用滑環，可靠性好，但控制難度也最大，對于某些高精度系統要求反轉瞬間角度誤差很小。

目前已發展出許多種電機控制策略，包括PID(proportional－integral－differential)控制、模糊控制和神經網絡［7～10］等，往往采用閉環控制。PID控制是工程上最常用的一種控制方法，其結構簡單并易于實現，但一般難以滿足某些高精度系統的性能要求，而其它的現代控制方法雖然從理論上講在某種程度上能夠提高控制性能，但在工程實際應用中卻增加了系統的復雜性而降低了可靠性。常見的電機正反轉控制主要是針對速度控制，而反轉瞬間角度的控制精度不高，大多數是從硬件上解決的［11－12］，需要設計特殊的電路結構;也有采用現代控制策略的［13－14］，而對于旋轉調制式捷聯慣導系統，電機轉速一般在幾度每秒至幾十度每秒之間，這些控制策略在中低轉速的控制系統中相比于常規PID控制并不能體現出明顯優勢，運算量也相對較大，在實時運算中往往需要相應的硬件設計［15］。

針對上述背景，給出了一種相比于其它的控制算法更為簡單易行的，應用于高精度旋轉調制捷聯慣導系統的直流電機正反轉控制方法，只需具有位置反饋的單閉環控制回路，采用PID控制與開環控制相結合的控制技術和系統調試方法，在仿真的基礎上對某型采用撓性器件的雙軸旋轉調制式捷聯慣導系統進行了實際調試，調試結果達到了系統精度要求。

1 系統介紹

雙軸旋轉調制式捷聯慣導系統由兩個獨立的單元體構成，系統實物圖如圖1所示。坐標系定義如圖2所示，單元體1旋轉軸與機體軸Z方向一致，單元體2旋轉軸與機體軸Y負方向一致。每個單元體內有兩個撓性陀螺和兩個撓性加計，對應敏感軸的x、y方向。開機后電機首先尋零，然后兩個單元體同時正反轉，將敏感軸的角速度和加速度分解到機體軸上，其中單元體1經旋轉分解后得到X、Y軸導航數據，單元體2經旋轉分解后得到Z軸導航數據。單元體1調制水平方向的陀螺漂移，單元體2調制垂直方向的陀螺漂移。這種系統結構仍然使用原有的慣性器件并且不改變已經成熟的導航算法，采用機械旋轉的方式達到減小陀螺漂移的目的，基本上可以使系統的導航精度提高一個量級。

圖1 旋轉調制捷聯慣導系統實物圖Fig．1 The rotation-modulation strap-down inertial navigation system

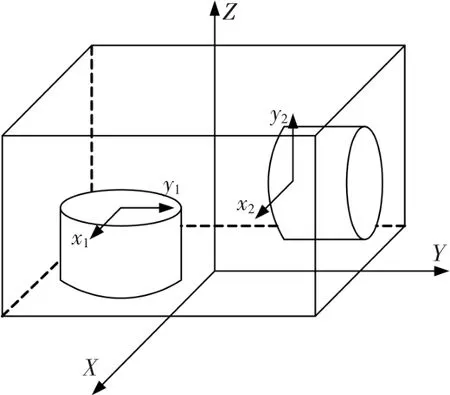
圖2 系統結構示意圖Fig．2 Structure of RM SINS

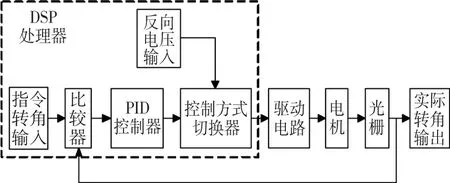
圖3 旋轉控制系統框圖Fig．3 Flow of rotation control

為了最大程度減小系統復雜程度，電機旋轉控制系統采用具有位置反饋的單閉環結構，如圖3所示。系統采用國產J80LYX01F1型永磁直流力矩電機，參數為:轉動慣量約為0.001 kg·m3(包含負載)，電樞電阻為3.5 Ω，電樞電感為2.6 mH，力矩系數為0.08 N·m/A，靜摩擦力矩為0.045 N·m。DSP的型號為TMS320F2812，采用英國Renishaw的光柵，其分辨率為1.44″，刻線精度 ±3.6″。電機的旋轉控制算法在DSP芯片內完成，其輸出經驅動電路放大后給到電機，再通過光柵讀出轉角反饋給DSP。

2 旋轉控制誤差對導航的影響

在理想情況下，敏感軸陀螺漂移經過旋轉分解后被調制成正弦或者余弦振蕩，如式(1)所示，其中Δεx1、Δεy1表示單元體1 的敏感軸漂移，ΔεX、ΔεY表示單元體1的機體軸漂移。

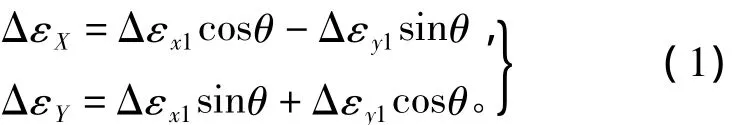
在實際情況下，旋轉控制誤差會導致機體軸上存在不可調制漂移，表現出的形式為:在電機平穩旋轉階段，旋轉控制誤差類似于噪聲，這會增大機體軸角速度上的隨機游走;在電機反轉期間，旋轉控制的超調誤差使得敏感軸漂移在這段時間內不能被完全調制，經過長時間累計后可造成導航誤差。

目前，從工程經驗的角度提出的控制要求是:平穩旋轉時的角度誤差小于10″，反轉時的最大角度誤差小于30″。該誤差對于導航的影響可以忽略不計。

3 旋轉控制算法流程

控制算法流程圖如圖4所示。第n時刻的指令轉角為

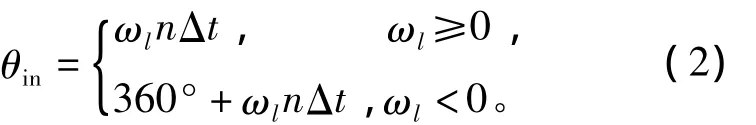
其中:ωl為理想轉速;Δt為采樣周期。

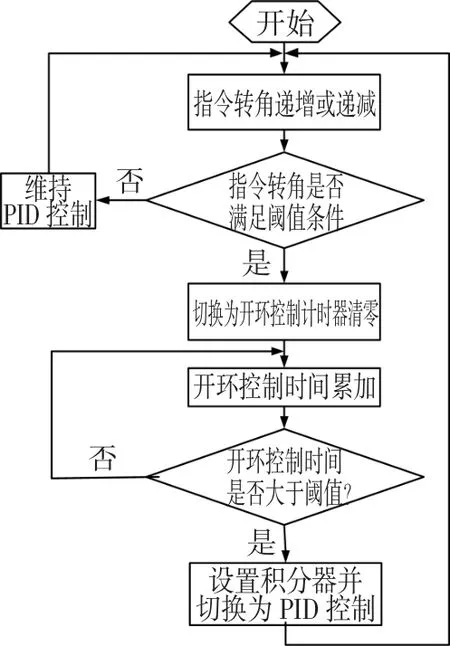
圖4 算法流程圖Fig．4 Computation scheme of rotation control

為了保證平穩旋轉時的精度并具有足夠的抗干擾性，在電機勻速旋轉時采用PID控制方式。當指令轉角θin在正轉過程中滿足θin＞θ1或在反轉過程中滿足 θin＜ θ2(其中 θ1略小于360°，θ2略大于0°)，即認為電機開始反轉，控制方式切換為開環控制方式，否則繼續維持PID控制方式。在開環控制方式中，在電機兩端施加幾伏到二十幾伏的電壓，并且當開環控制計時器的累計時間大于閾值(一般為1～10 ms)時再切換回PID控制，并設置積分器的初值，電機又開始勻速轉動。

4 系統調試方法

4.1 系統模型

系統模型框圖如圖5所示，其中:P、I、D分別為比例、微分和積分控制器參數;U為控制電機的電壓;ω為電機的角速度;L為電樞電感;R為電樞電阻;I為電機的電流;Cm為力矩系數;M為輸入給電機的控制力矩;J為電機的轉動慣量;B為粘滯摩擦系數;Mf庫倫摩擦力矩;Ce為反電勢系數。系統模型中包括控制器模型、電機模型和光柵模型。其中控制器模型包括PID控制器和控制方式切換器，電機模型［16］的表達式為

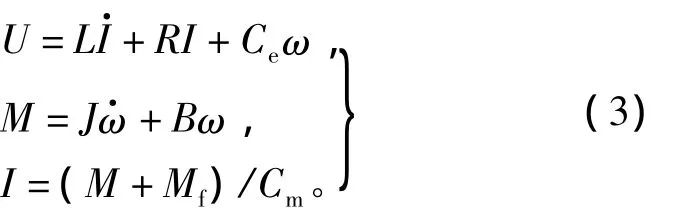
其中光柵模型即為積分器。

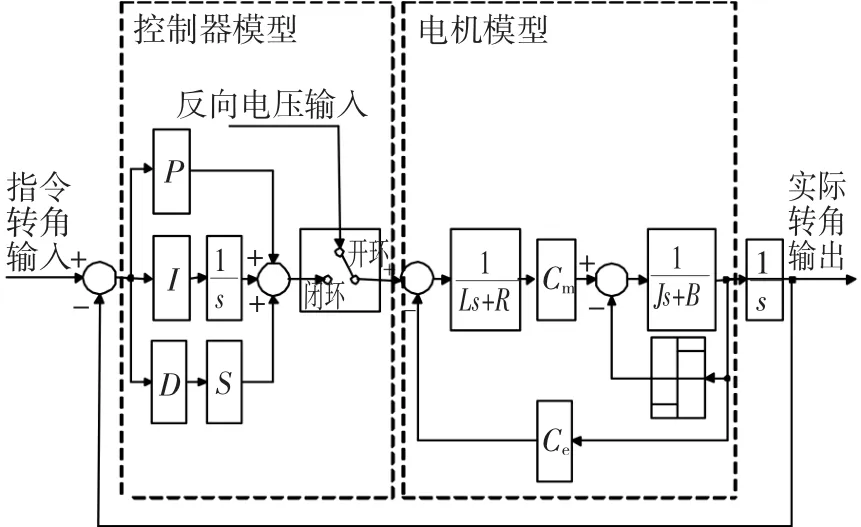
圖5 系統模型框圖Fig．5 The system rotation control model

實際系統的轉動慣量J和粘滯摩擦系數B一般很難估計，可以把系統近似為一階模型并進行參數辨識［17］。

4.2 PID參數的整定

PID參數的整定采用Z－N整定法，PID控制器的輸出為

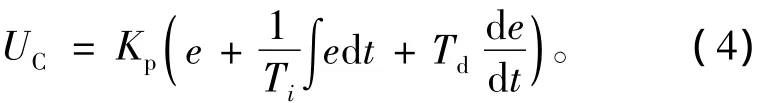
其中:e為角度誤差;Kp為比例增益;Ti為積分時間常數;Td為微分時間常數;這里令P=Kp，I=Kp/Ti，D=KpTd。系統閉環，令I=0，D=0，給電機輸入一單位階躍電壓，逐漸增大P，直至電機轉角出現等幅振蕩，記下此時的比例增益Pu和振蕩周期Tu，則Ti=0.5Tu，Td=0.125Tu，P=0.6Pu。該參數整定方法只用在仿真中，實際中參照仿真的結果。

4.3 反轉瞬間的開環控制

電機反轉前轉換為開環控制，對電機施加1～10 ms的反向電壓，其大小記為UT。由圖4可知，若不考慮摩擦和反電動勢，忽略電樞電感，則輸入電壓U和控制力矩M之間的關系近似為

在仿真和實際中再微調UT直至控制方式由開環控制切換到PID控制的時刻電機轉速盡量接近反轉后平穩旋轉時的速度。

4.4 反轉后PID控制器的設置

PID控制器中的積分器具有記憶功能，在電機平穩旋轉時，積分器的輸出用于抵消阻力。所以在電機反轉后要根據阻力情況設置積分器中的值，使之快速過渡到平穩旋轉時的穩態值。

由圖4可知電機平穩旋轉時的阻力由靜摩擦力矩、粘滯摩擦力矩和反電動勢等效力矩三部分構成，其中后兩項與電機的轉速成正比，所以積分器穩態值的計算公式為

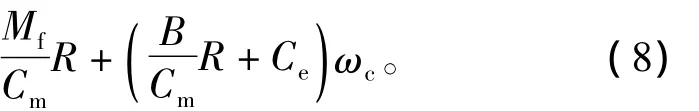
在電機即將反轉時加反向力矩MT，所加時間為ΔT，電機平穩旋轉時的轉速大小為ωc，根據剛體轉動動力學原理，則有

由式(5)和式(6)可得到反向電壓UT的近似計算公式為

在仿真或實際中，可以根據式(8)設置控制方式轉換后的積分器初值，若摩擦力矩和反電勢系數很小，也可直接將積分器清零。

5 系統仿真結果

針對國產J80LYX01F1型永磁直流力矩電機進行了SIMULINK仿真，開環控制時間為1 ms，電機平穩旋轉時的轉速為11.25°/s，由式(7)估算的反向電壓的大小為17.2 V，仿真中是在電機反轉前1 ms加了大小為18 V的反向電壓，轉為PID控制時根據式(8)將積分器初值大小設為1.97 V。

圖6給出了用常規PID控制與新方法的仿真結果對比，圖6(a)為角度誤差的對比，圖6(b)為角速度的對比。采用常規PID控制時，電機在平穩旋轉時無穩態誤差，反轉瞬間的最大角度誤差為174″，角速度超調為56.4%，調節時間約25 ms;采用新控制方法后，電機在平穩旋轉時無穩態誤差，反轉瞬間的角度誤差小于30″，角速度超調為1.5%，調節時間小于20 ms。

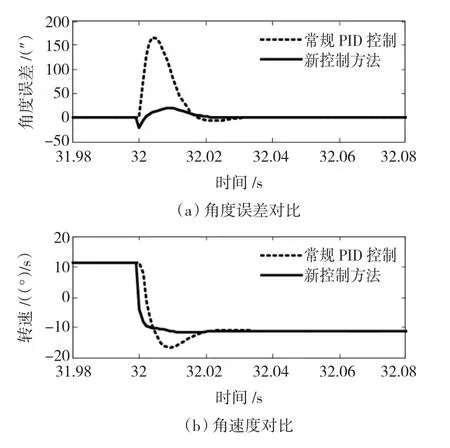
圖6 常規PID控制與新方法的仿真結果對比Fig．6 Comparing simulation result of common PID with the new methods’

6 實際系統調試結果

在實際中對上述J80LYX01F1型電機進行調試，開環控制時間為1 ms，電機平穩旋轉時的轉速為11.25°/s，實際中是在電機反轉前1 ms加了大小為18 V的反向電壓，轉為PID控制時積分器的設置參考仿真的結果進行了微調。電機在平穩旋轉時穩態誤差的標準差為2.3″。

圖7給出了用常規PID控制與新方法的實際調試結果對比。采用常規PID控制時，反轉瞬間的最大角度誤差為180″，反轉的調節時間約為40 ms，角速度超調為157.8%;采用新控制方法后，反轉瞬間的角度誤差小于20″，反轉的調節時間小于40 ms，角速度超調為1.6%，反轉過程非常平穩，滿足系統精度要求。

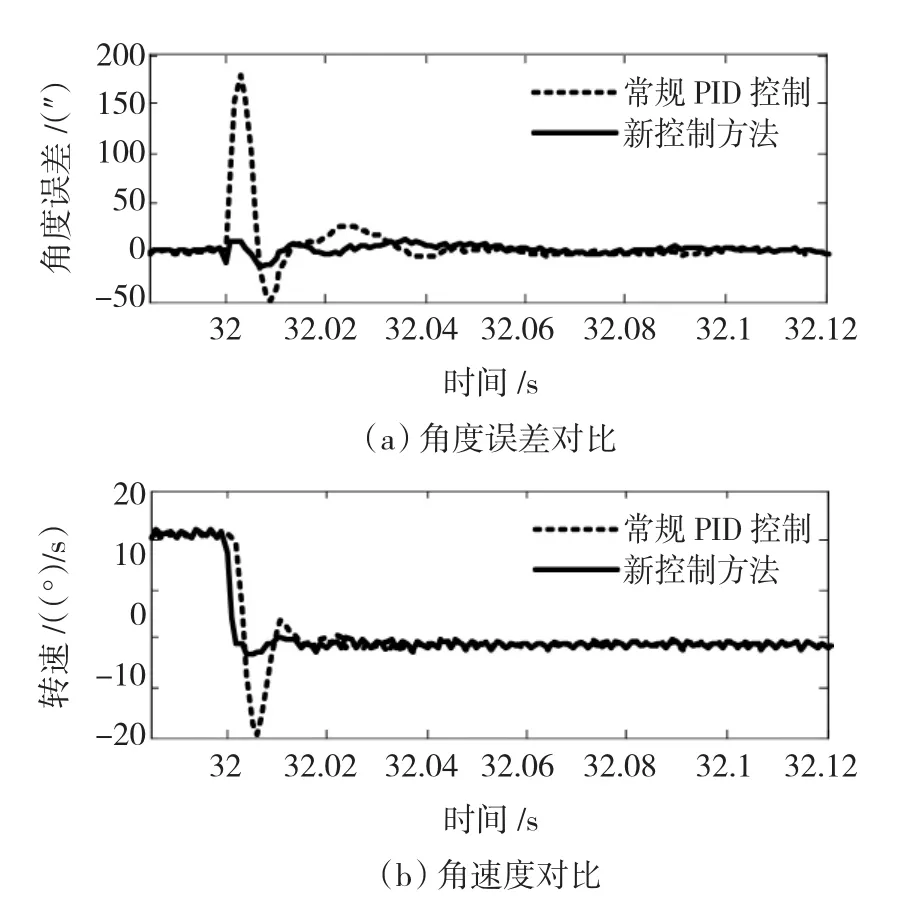
圖7 用常規PID控制與新方法的實際調試結果對比Fig．7 Comparing actual result of common PID with the new methods’

7 結論

系統仿真結果和實際系統的調試結果表明，這種應用于高精度旋轉調制捷聯慣導系統的PID控制與開環控制相結合的直流電機正反轉控制方法是有簡單而有效的，這體現在:

1)使反轉瞬間的角度誤差降至30″以下，角速度超調小于2%，實現了電機的平穩反轉。

2)與常規PID控制方法相比角位置和角速度精度均大幅度提高。

3)采用軟件方法解決了如何在兩種控制方式間進行切換的問題，保證了控制方式轉換時的平穩過渡。

［1］陀螺儀與慣性導航專業情報網．國外慣性技術手冊［M］．北京:國防工業出版社，1983:235－238．

［2］FULFROST J，CHECCO W J．Ring laser gyro navigator for surface combatant ships［J］．IEEE PLANS，1984:348 －357．

［3］LEVISON E，TER Horst J，WILLCOCKS M．The next generation marine inertial navigator is here now［C］//1994 IEEE Position location and Navigation Symposium，April 11－15，1994，Las Vegas，USA．1994:121 －127．

［4］高亞楠，陳家斌，楊亭鵬．捷聯式光纖陀螺羅經系統誤差分析［J］．北京理工大學學報，2005，25(5):423－426．

GAO Yanan，CHEN Jiabin，YANG Tingpeng．Error analysis of strapdown optic fiber gyro compass［J］．Journal of Beijing Institute of Technology，2005，25(5):423 －426．

［5］龍興武，于旭東．激光陀螺單軸旋轉慣性導航系統［J］．中國慣性技術學報，2010，18(2):149－153．

LONG Xingwu，YU Xudong．Single-rotating inertial navigation system with ring laser gyroscope［J］．Journal of Chinese Inertial Technology，2010，18(2):149－153．

［6］LEVINSON E，MAJURE R．Accuracy enhancement techniques applied to the marine ring laser inertial navigator(MARLIN)［J］．Journal of The Institute of Navigation，1987，34(1):64－86．

［7］YASUHIKO Dote．Application of modern control techniques to motor control［J］．Proceedings of IEEE，1988，76(4):438 －455．

［8］張凌云，賴豪杰．先進控制理論及策略在電機控制中的應用［J］．電機技術，2005，2:38－41．

ZHANG Lingyun，LAI Haojie．Application of advanced control theories and strategies in motor control［J］．Electrical Machinery Technology，2005，2:38－41．

［9］HU B G，MANN G K I，GOSINE R G．New methodology for analytical and optimal design of fuzzy-PID controllers［J］．IEEE Transactions on Fuzzy Systems，1999，7(5):521－539．

［10］ADHAVAN B，KUPPUSWAMY A，et al．Field oriented control of permanent magnet synchronous motor(PMSM)using fuzzy logic controller［J］．Recent Advances in Intelligent Computational Systems，2011，9:587 －592．

［11］周鳳爭，沈建新．帶正反轉功能的通用型無刷直流電機控制器設計［J］．2007，10:43－44．

ZHOU Fengzheng，SHEN Jianxin．Design of universal PM BLDC motor controller with reversion function［J］．Micromotors Servo Technique，2007，10:43 －44．

［12］胡海云．基于DSP的無刷直流電機控制系統研究［D］．上海:上海交通大學，2003．

［13］XIE Zengrong，LIANG Deliang．Research on control system of linear PM brushless DC motor based on single neuron PID［C］//ICEMS 2005，Sept 27－29，2005，Nanjing，China．2005:385－387．

［14］嵇艷鞠，李肅義．基于單神經元自適應PID的PLC直流電機控制系統［J］．吉林大學學報，2007，25(5):526 －532．

JI Yanju，LI Suyi．Control system of PLC DC electric motor based on single neuron self-adaptive PID controller［J］．Journal of Jilin University，2007，25(5):526－532．

［15］JEFFREY R，MOUNTAIN．Fuzzy logic motor speed control with real-time interface using an 8-bit embedded processor［C］//42nd South Eastern Symposium，March 7 －9，2010，Texas，USA．2010:307－312．

［16］GEHMLICH D K，KUO B C．直流電動機及其控制系統［M］．哈爾濱:哈爾濱工業大學出版社，1984:64－66．

［17］薛定宇．控制系統計算機輔助設計－Matlab語言與應用:2版［M］．北京:清華大學出版社，2006:263－267．