基于正交編碼的高頻地波雷達信號的設計

李 超 張 寧

（哈爾濱工業大學電子工程技術研究所，黑龍江 哈爾濱 150001）

引 言

解決電離層雜波折疊就是要提高信號的不模糊距離，使得電離層雜波處在信號的不模糊距離之外，無法對探測距離內產生折疊效應。雖然加大脈沖周期可以增大不模糊距離，卻會導致占空比下降，從而使得發射機功率降低無法實現遠距離探測。若采用多脈沖正交信號，由于脈沖之間相互正交，即其互相關函數為零，回波信號經過脈沖壓縮之后，只對自身脈沖產生距離譜，因此，不產生距離模糊。簡單的正交編碼往往不具有好的自相關函數特性，無法達到雷達目標檢測的需求；若采用正交矩陣得到多脈沖編碼，雖然具有良好的旁瓣特性，但由于脈沖周期過長，容易產生多普勒模糊，無法滿足海空兼容探測。因此，需要進行正交編碼波形優化設計。

發射波形優化設計是眾多學者近年來的研究熱點。Deng［1-2］研究了基于模擬退火的正交波形設計，主要是以互相關和自相關旁瓣能量最小為目的。在Deng的研究工作之后，出現了一系列正交波形設計方法，其中主要有遺傳算法、整數非線性規劃、最小互熵法、相位逗留法等，這些方法被廣泛用于多輸入多輸出（MIMO）雷達［3-4］和分組雷達信號的設計。然而，這些雷達均采用頻分復用來發射多頻信號。對于高頻地波雷達系統來說，頻分復用信號對設備的線性度要求很高，且信噪比損失較大，時分復用方式是首選。本文主要研究高頻地波雷達時分復用方式下正交編碼的設計，其各個頻段采用的信號形式完全相同，要求每個頻段內信號的各個脈沖正交。

高性能的雷達系統通常要求峰值旁瓣比達到-30dB以上，在一些特殊的場合有可能提出超低旁瓣的要求。當優化設計的編碼仍無法滿足系統對旁瓣的需求時，就需要采用信號處理的手段來降低旁瓣。目前國內外關于旁瓣抑制濾波器的設計方法很多，如窗函數加權法［5，6］，最小均方誤差（LMS）［7］，最小的線性規劃法，遞歸最小平方法（RLS）［8］以及近年來興起的神經網絡算法等。早在1971年，Rihaczek和Golden［9］就利用反相濾波器對Barker碼進行抑制，取得了較好的效果，但由于只考慮對Barker碼的抑制，限制了其廣泛應用。G.D.Cain［10］等提出了基于反相濾波的最優碼搜索。隨后Erikmat［11］又提出了利用無限長脈沖響應（IIR）來設計反相濾波器。Robert C［12］詳細地分析了Erikmat的算法并利用在旁瓣抑制方面。

針對高頻地波雷達的特殊需求來構建代價函數，采用遺傳算法設計時分復用的正交雙脈沖信號，獲得了具有理想自相關函數旁瓣和互相關函數峰值的信號。并對得到的正交編碼采用反相濾波算法進行了旁瓣抑制。通過仿真實驗比較，可以看出此算法的抑制性能更為有效。即使在較大多普勒偏移下仍有較低旁瓣，完全可以滿足高頻地波雷達系統需求。

1.電離層雜波產生的折疊干擾問題

電離層雜波折疊［13，15］是指發射信號以一定角度到電離層向外傳播，由于信號總路徑必定經過了由脈沖重復間隔決定的最大探測距離。因此，雷達會將前幾個脈沖的回波在當前周期中接收回來，產生距離模糊。由于存在著距離模糊，與目標同一距離單元上接收到的雜波在時間上是重疊的，其中包括近程的強雜波。高強度的折疊雜波完全有可能淹沒目標，尤其是復雜低空環境中的弱目標。如果系統無法檢測折疊雜波中的目標，就會發生目標丟失現象，影響到雷達的探測性能。

微波雷達工作在微波段，信號可以穿透電離層雜波，因此，電離層雜波對微波雷達探測目標幾乎沒有影響。而對于高頻地波雷達來說，其作用距離為300～400kg.幾千公里外的電離層雜波折疊，對這一區域目標產生嚴重的干擾。因此，電離層雜波折疊問題可以說是高頻地波雷達波形設計中必須要考慮的問題。

從波形設計的角度解決高頻雷達的電離層雜波折疊干擾問題，方法主要有兩種:

1）單脈沖疊加相位旋轉。文獻［13］針對高頻雷達中雜波折疊問題，提出了一種脈間相位編碼波形，將雜波搬移到無目標存在的多普勒區間，使原本掩蓋的目標顯現出來。從而解決了電離層雜波的折疊干擾問題。但是這種方法需要目標的先驗知識。

2）正交多脈沖序列。文獻［14］用Frank矩陣等正交矩陣構造正交多脈沖互補編碼，這種編碼脈壓信號具有零旁瓣特性，且能將不模糊距離推遠到幾千公里以外，避免了電離層對回波產生影響。

但是以上兩種方法都有其自身缺陷，單脈沖序列脈沖壓縮信號往往具有過高旁瓣，無法滿足我們的檢測需求。正交互補序列由于其互補特性，有著理想的脈壓主旁瓣比，但是其分段互補的信號結構，使得信號的重復周期過長。當采用多頻分時探測模式時，無法進行海空兼容探測。為了同時滿足高頻地波雷達的這些需求，采用優化算法來設計雙脈沖正交信號，解決電離層雜波折疊問題，并保證足夠的占空比，同時其信號參數可以實現多頻模式下的海空兼容探測。雙脈沖正交信號的不模糊距離如圖1中Ru所示。

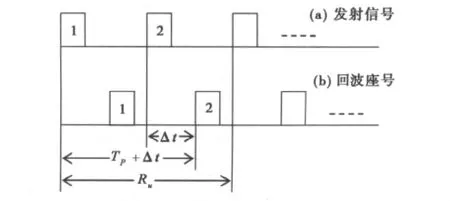
圖1 雙脈沖正交信號不模糊距離示意圖

如圖1所示，雙脈沖正交信號由兩個相互正交的脈沖組成一個信號周期。脈沖串（a）為發射信號，脈沖串（b）為回波信號。如果是單脈沖信號，就無法區分回波信號的第2個脈沖是發射信號的第1個脈沖的時延（Tp+Δt）還是第2個脈沖的時延（Δt）.因此，模糊距離為.但對于雙脈沖正交信號，由于兩個脈沖相互正交，即其自相關函數為零。回波信號經過脈沖壓縮之后，只對自身脈沖產生距離譜，因此不產生距離模糊。其最大不模糊距離為信號周期即Ru=2×=.因此，按照高頻地波雷達的檢測需求來構造代價函數得到雙脈沖正交信號就可以解決電離層雜波折疊的問題。

2.基于遺傳算法的正交相位編碼

利用遺傳算法設計正交碼，就是針對實際系統綜合考慮多方面構造出代價函數，并最小化代價函數得到編碼序列。

2.1 代價函數的構造

為了滿足海空兼容探測的需求，主要研究了雙脈沖正交相位碼。設有一對長度相同的有限二元序列，

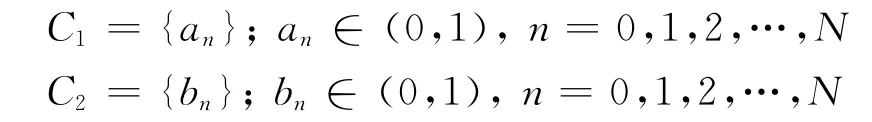
信號的自相關函數為式（1）和式（2），互相關函數為式（3）.

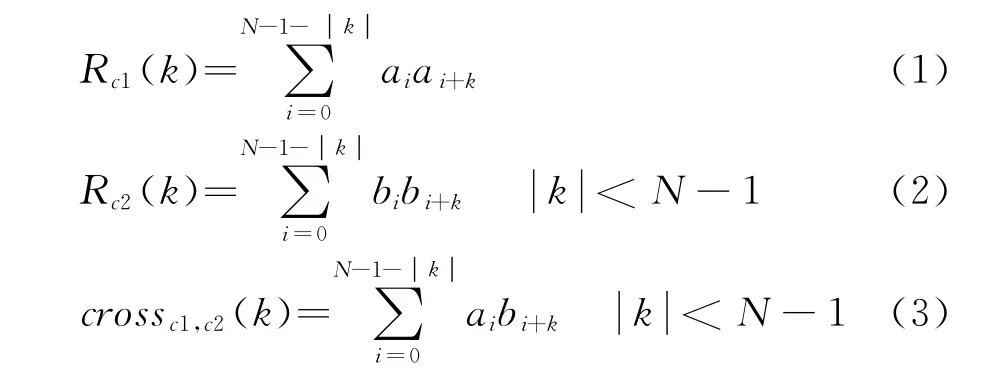
碼元信號需要具有以下特性:

1）每個脈沖都具有較低的峰值旁瓣電平PSL

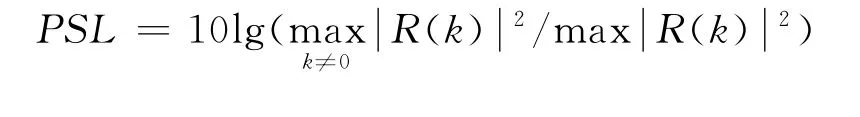
2）每個脈沖具有較低積分旁瓣電平ISL

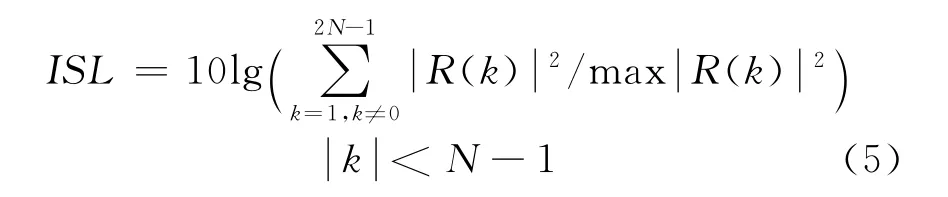
3）兩個脈沖的互相關函數峰值較低（低于各自的自相關旁瓣）

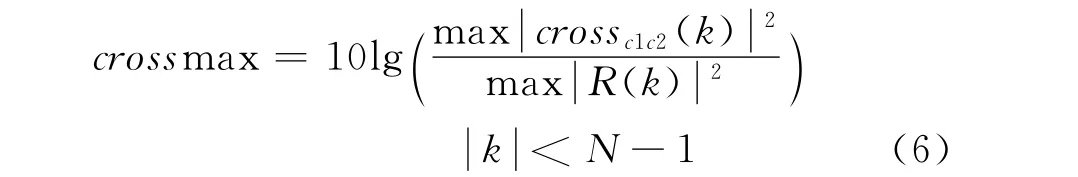
需要說明的是，這里對互相關函數用自相關函數峰值進行歸一化，若歸一化的互相關函數峰值低于自相關函數旁瓣，則表明兩個脈沖正交，信號重復周期（兩個脈沖周期）內不存在距離模糊現象，信號的最大不模糊距離為兩個脈沖周期。

4）兩個脈沖的互相關函數積分旁瓣電平較低

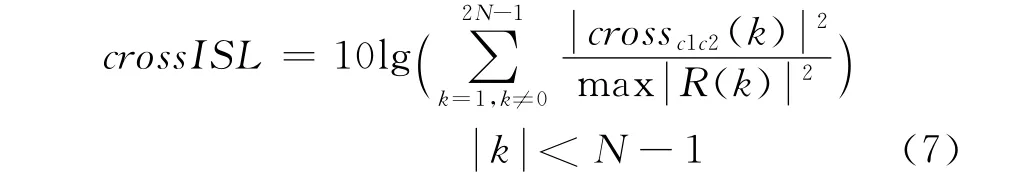
將以上各個約束函數以罰函數的形式附加到代價函數中，則有

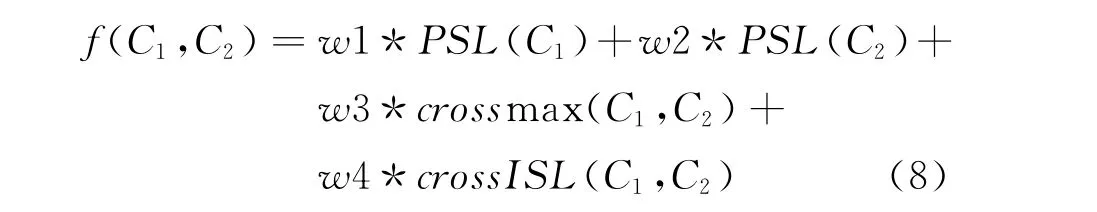
式中:［w1，w2，w3，w4］是各個約束函數的加權系數，可以通過訓練的方法得到，也可以根據優化要求自行設置。

2.2 遺傳算法設計正交編碼步驟

1）編碼

把一個問題的“可行解”從“解空間”轉換到遺傳算法所能處理的“搜索空間”的轉換方法就稱為編碼。近年來許多學者研究證明二進制碼比十進制碼具有更強的搜索能力。因此，二進制編碼是遺傳算法中最主要的一種編碼方式。

由于需要優化設計的二相碼本身就是二進制編碼，因此可以直接將它們表示成遺傳空間的基因型數據。這里把兩個脈沖的編碼放在一個行矩陣中，看成一個個體。即S=［C1C2］=sn，sn∈ （0，1），n=1，2，…，2 N，N為二相正交碼一個脈沖內的碼元個數。S前一半碼元為第一個脈沖C1，后一半碼元為第二個脈沖C2.

2）初始群體的生成

由于遺傳算法的群體型操作需要，必須為遺傳操作準備一個由若干“初始解”組成的初始群體。若初始種群數量為NIND個，每個脈沖內碼元個數為N，采用隨機二元碼做編碼。則初始種群為NIND×2 N的矩陣。

3）計算適應度

在完成編碼和初始化種群后，將種群中每個個體的編碼帶入代價函數中計算其適應度值。計算的適應度值為后面的操作提供依據。

4）選擇

根據第三步計算出的適應度值對種群中的個體進行選擇，適應度高的個體遺傳到下一代的概率就較大。常用的選擇算子有輪盤賭、隨機競爭、最佳保留等。本文選擇隨機遍歷法進行搜索。

5）交叉

在遺傳算法中，交叉是產生新個體的主要手段，將第四步選擇的個體進行離散重組和交叉。

6）變異

變異是按位進行的，即把某一位的內容進行變異。變異操作是十分微妙的操作，它需要和交叉操作妥善配合使用，目的是挖掘群體中個體的多樣性，克服有可能陷于局部解的弊病。

7）終止

當完成遺傳的代數后程序終止。

2.3 設計結果及性能

按照以上算法和步驟，進行仿真實驗，優化設計正交相位編碼，遺傳算法仿真參數為:初始種群數量100，迭代最大次數200，代溝0.9，交叉概率0.7，為了保證信號的正交性，需要互相關函數峰值小于自相關函數旁瓣，因此權值設為w= ［1131］，脈內碼元個數N為32.

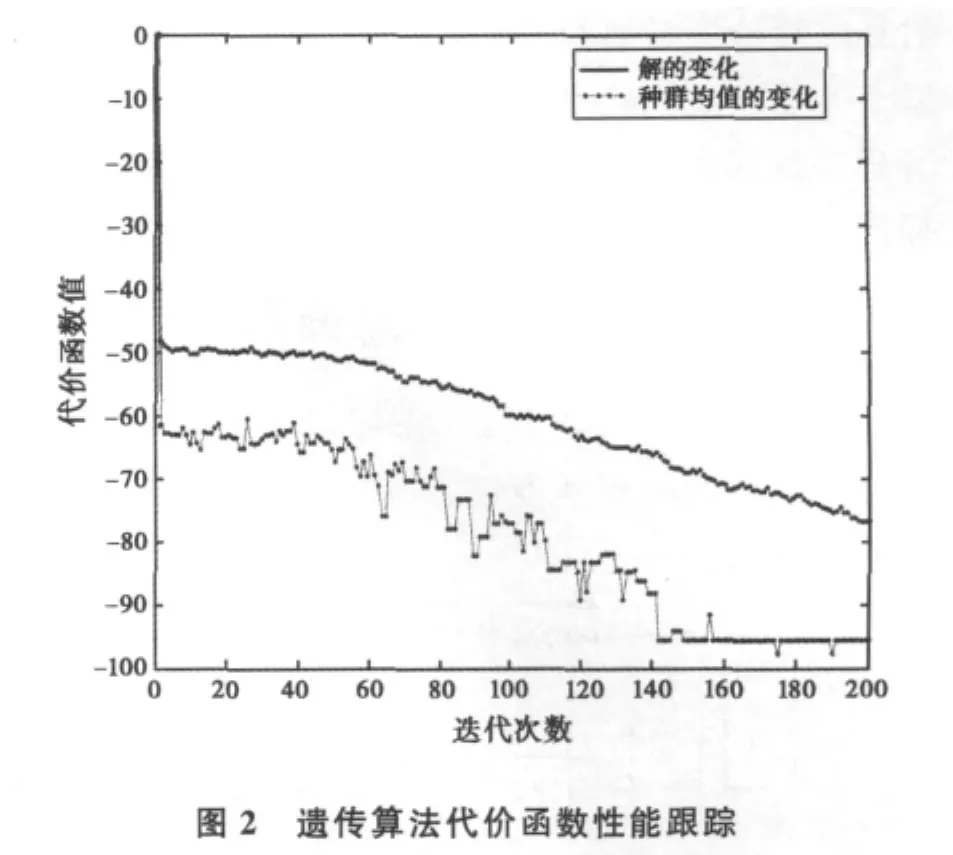
圖2為遺傳算法200次迭代的性能跟蹤。可以看出種群均值和最優解逐漸收斂，迭代次數越多，得到解的各項性能就越優，當收斂到一定程度，解的各項性能不隨迭代次數增加而變化，實驗證明迭代200次可以得到最優解。

每次運行遺傳算法得到的最優解不盡相同，但是其自相關和互相關特性相差無幾，這些最優解都可以作為高頻地波雷達的編碼。這里分析其中一組碼元的性能。

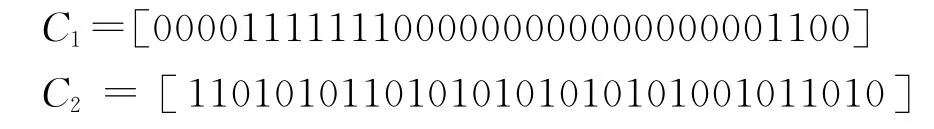
其自相關函數與互相關函數圖如3和4所示。

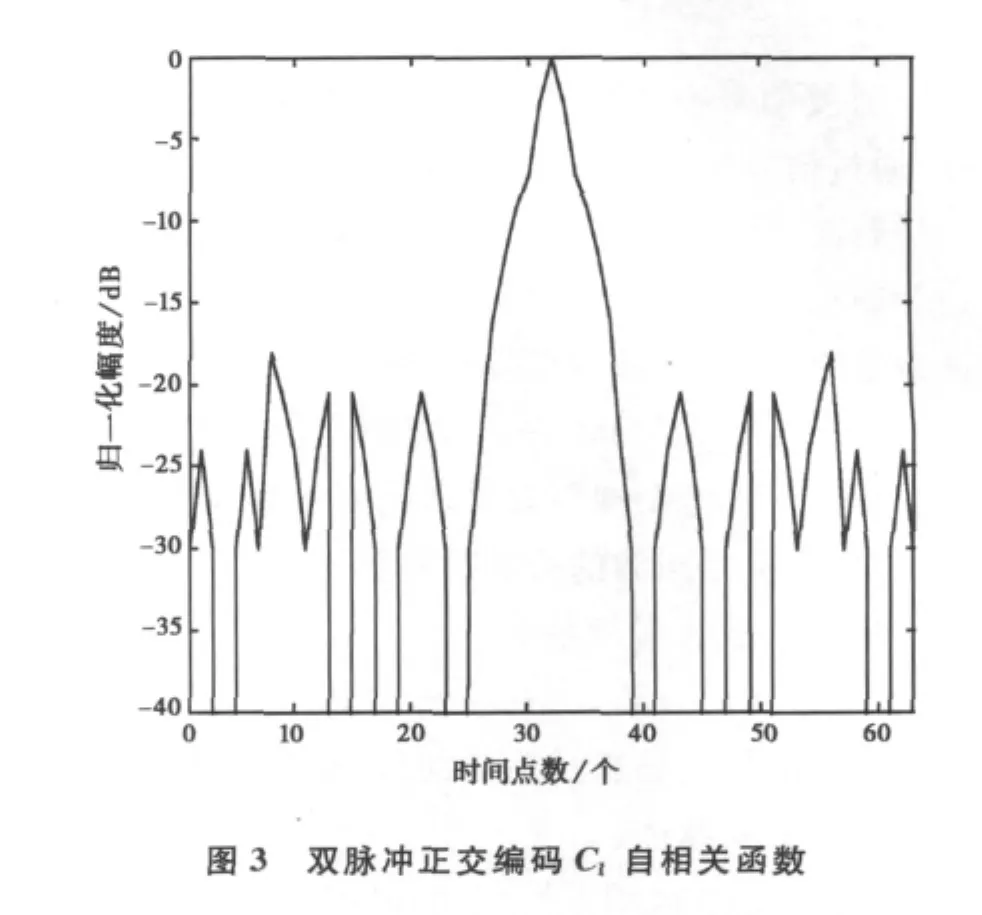
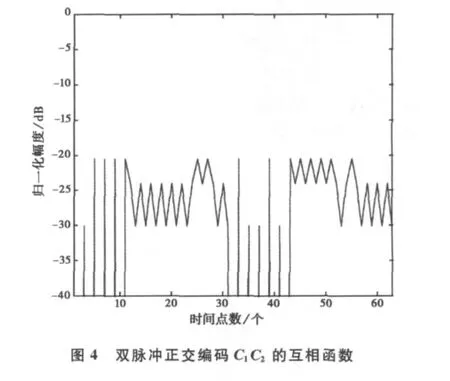
從圖4可以看出，兩個脈沖的互相關函數峰值-20dB，小于各脈沖的自相關峰值-18dB，這樣就不會產生距離模糊現象。最大不模糊距離為兩個脈沖周期。因此，采用遺傳算法可以得到解決距離模糊現象的正交相位編碼。但是高頻地波雷達對脈壓信號的峰值旁瓣有較高的要求，通常需要在-30dB以上。而通過優化算法得到的正交編碼自相關函數旁瓣大約都在-20dB左右，因此必須要進行旁瓣抑制。

3.正交編碼信號的旁瓣抑制

在雷達信號的接收端，需要對回波信號進行處理得到需要的距離速度譜。雙脈沖的信號處理方法如圖5所示。

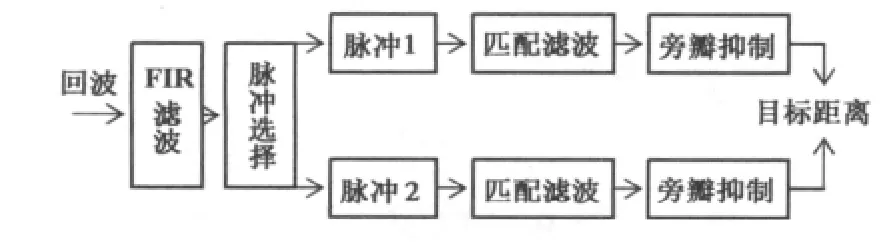
圖5 雙脈沖信號的處理方法

回波信號經過降采樣和濾波之后，進行脈沖選擇，通過信號識別算法判斷出回波是第幾個脈沖，然后進行匹配濾波，得到距離譜，根據目標特性，選擇適當的積累時間進行脈沖積累得到速度譜。為了提高信號的分辨力，進一步降低旁瓣，必須進行旁瓣抑制，本文采用Erikmat提出的反相濾波算法［11］，仿真實驗證明其旁瓣抑制效果遠遠好于其他算法。

3.1 基于反相濾波的旁瓣抑制算法

回波信號的Z變換為

算法的核心思想是信號經過旁瓣抑制濾波器之后應為零旁瓣脈沖。

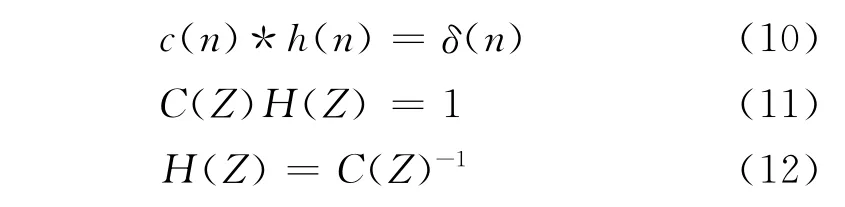
Mercer指出，具有+1，-1系數的多項式至少有一個零點在單位圓上或單位圓外。因此，C-1（z）就有極點在單位圓外，不是穩定因果系統。Robert在文獻［12］中把C（z）分成兩部分:

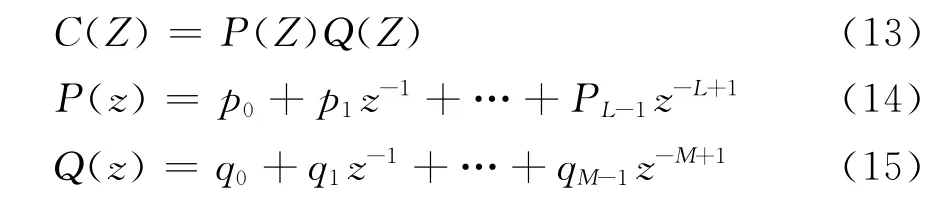
信號長度N=M+L-1.這里P（z）為C（Z）所有單位圓內零點所構成的多項式。Q（z）為所有C（Z）單位圓外零點構成的多項式。

這樣濾波器P-1（z）是穩定的。當信號通過如圖6所示P-1（z）的部分時就去掉了單位圓內零點所產生的旁瓣，輸出信號為F（z），理論上F（z）=Q（z）.Q（z）的時間反向為

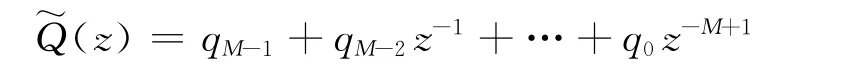
（Z）的零點是Q（Z）的零點的倒數，其零點都在單位圓內，濾波器響應是穩定的。編碼序列經過濾波器P-1（z）后，進行時間反向操作，然后再經過（Z）濾波器，得到的期望響應為沖擊單位抽樣序列δ（n）.這樣，通過兩個濾波器級聯的方式，就可以完全的去處旁瓣。

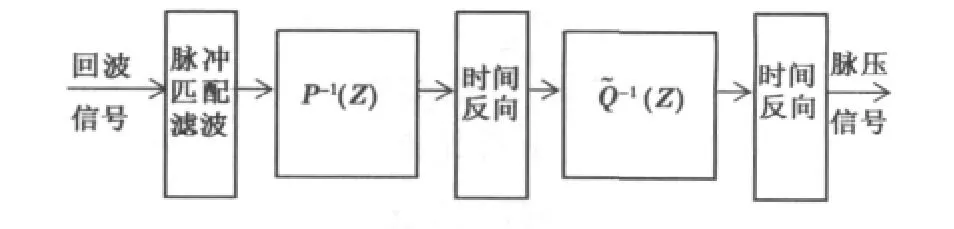
圖6 反相濾波器結構示意圖

3.2 算法性能仿真實驗

將正交編碼進行匹配濾波，然后將匹配濾波得到的自相關函數轉換成Z變換序列，求序列的零點。用在單位圓內的零點構造P-1（z）濾波器；將單位圓外的零點求倒數后構造（Z）濾波器。這樣就可以得到反相濾波器組。

仿真實驗采用脈沖寬度為20μs，編碼長度為32，載頻為14MHz（高頻地波雷達通常為3～15 MHz）。將輸入信號按照圖6的方式通過濾波器組就得到旁瓣抑制結果。從表1可以看出經過旁瓣抑制后脈沖壓縮信號峰值旁瓣非常低。

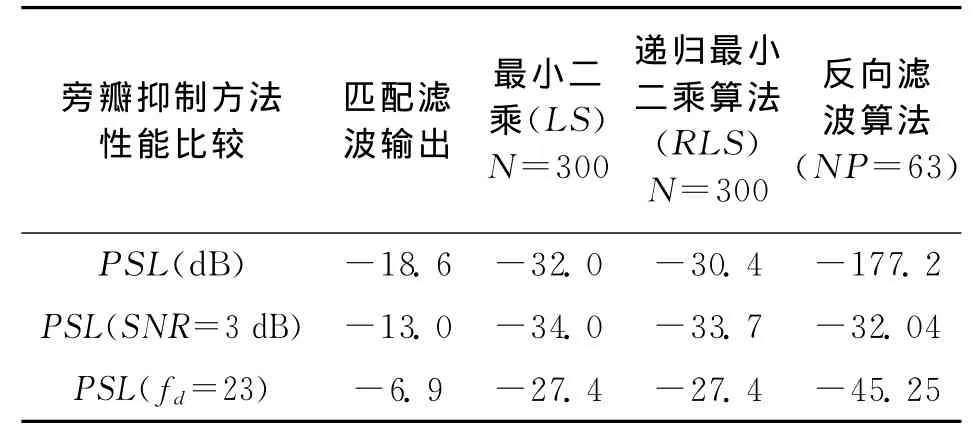
表1 幾種旁瓣抑制方法的比較

表1將該算法與目前常用的算法進行了比較。可以看出，反相濾波算法在噪聲背景下的濾波性能一般，但是也能夠滿足高頻地波雷達信號檢測的需要。而在其他情況下要遠遠優于其他算法。尤其是在多普勒頻移較大的時候fd=23（載頻為14 MHz，目標速度為250m／s）也具有-45dB的峰值旁瓣。

圖7為目標在不同速度下，碼反相濾波算法的旁瓣抑制性能，可以看出，即使在速度較高的情況下也能有較低的旁瓣，高速目標的旁瓣也能低于-40 dB，其多普勒容限性較好。

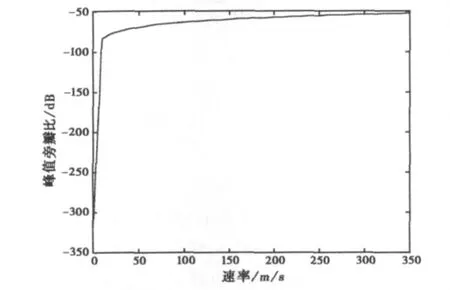
圖7 碼反相濾波算法的多普勒容限性

4.結 論

采用遺傳算法設計正交編碼，碼元信號具有良好的自相關和互相關特性，解決了高頻地波雷達電離層折疊的問題。為了進一步降低自相關函數旁瓣，研究了碼反相濾波算法，仿真實驗證明算法有著較好的抑制效果且多普勒容限性好，未來將對其的工程應用進行更細致的研究。

［1］DENG H.Poly Phase code design for orthogonal netted radar systems［J］.IEEE Transactions on Signal Processing，2004，52（11）:3126-3135.

［2］DENG H.Discrete frequency-code waveform design for netted radar systems［J］.IEEE Signal Processing Letters，2004，11（2）:179-182.

［3］LI Jian，XU Luzhou，STOICA P.Range compression and waveform optimization for MIMO radar:a cramerrao bound based study［J］.IEEE Transactions on Signal Processing，2008，56（l）:218-232.

［4］李樹鋒，張履謙.基于完全互補序列的正交MIMO雷達二維DOA估計［J］.電波科學學報，2009，25（4）:617-623.LI Shufeng，ZHANG Lvqian.Two dimensional DOA estimation for orthogonal MIMO radar based on complete complementary sequence［J］.Chinese journal of radio science，2009，25（4）:617-623.（in Chinese）

［5］KRETSCHMER F F，WELCH L R.Sidelobe reduction techniques for polyphase pulse compression codes［C］／／IEEE International Radar Conference.Alexandria，VA，USA，2000:416-421.

［6］LUSZCZYK M，MUCHA D.Kaiser-bessel window weighting function for polyphase pulse compression code［C］／／Microwaves，Radar and Wireless Communications，2008:1-4.

［7］PARK S C and DOHERTY J F.A mini-max optimization approach to sidelobe suppression filter design［C］／／IEEE International Conference on Acoustics，speech，and signal processing，1996，6:3113-3116.

［8］張仕元，吳樂南.基于RLS的脈壓雷達數字旁瓣抑制濾波器設計方法［J］.測控技術，2006，25（7）:79-82.ZHANG Shiyuan，WU Lenan.Design of digital sidelobe suppression filter based on RLS method［J］.Measure and Control technology 2006，25（7）:79-82.（in Chinese）

［9］RIHACZEK A W and GOLDEN R M.Range sidelobe suppression for barker codes［C］／／IEEE Transaction on Aerospace and electronic system，1971，7:1087-1092.

［10］CAIN G D，YARDIM A，BOWLER A M，et al.Reducing pulse compression sidelobes by inversion amenable code selection［C］／／Radar Conference.Roman，2008:1-6.

［11］ERIKMATS O.Range sidelobe elimination for discrete-coded pulse compression systems［C］／／International Conference on Radar，1978:187-193.

［12］DANIELS R C and GREGERS-HANSEN V.Code inverse filtering for complete sidelobes removal in binary phase coded pulse compression system［C］／／Radar Conference，2005:256-261.

［13］CLANCY J T，BASCOM H F，HARTNETT M P.Mitigation of range folded clutter by a nonrecurrent waveform［C］／／IEEE Radar Conference，1999:79-83.

［14］KRETSCHMER F F，Jr，Gerlach K.Low sidelobe radar waveforms derived from orthogonal matrices［J］.IEEE Transactions on Aerospace and Electronic Systems，1991，27（1）:92-101

［15］萬顯榮，楊子杰，張景偉.高頻地波雷達距離混疊與距離模糊研究［J］.電波科學學報，2009，24（5）:891-894.WAN Xianrong，YANG Zijie， HANG Jingwei.Range aliasing and range ambiguity of HF surface wave radar［J］.Chinese Journal of radio science，2009，24（5）:891-894.（in Chinese）