流線型閉口箱梁斷面風荷載空間相關性試驗研究

張冠華，趙 林，葛耀君

(1.同濟大學 土木工程防災國家重點實驗室，上海 200092;2.遼寧省交通規(guī)劃設計院，沈陽 110005)

大跨度橋梁作為典型的空間線狀結構，傳統(tǒng)的抗風研究內容主要集中在空間線狀結構局部“點”的氣動力表達及其相應斷面的氣動參數識別等工作，一定程度上忽略或簡化了與結構響應密切相關的風荷載的空間相關性。目前，氣動力荷載的空間相關性僅僅考慮來流湍流的相關性，近似假定脈動風荷載的空間相關性與來流湍流一致，并服從指數律衰減趨勢。限于風特性觀測的條件和困難，描述湍流的空間相關特性的指數衰減因子一直按全橋跨完全相關而取最保守值［1]。伴隨著橋梁跨度不斷增加，結構對來流湍流的空間相關性將更為敏感，傳統(tǒng)的描述風荷載空間相關性的方法可能不再適用;同時來流湍流沿橋梁展向的流動也進一步影響氣動力的空間相關性;極端氣候條件下如臺風等所帶來的來流強湍流也會對氣動力的相關性產生較大影響。因此有必要深入研究風荷載相關性的影響因素，驗證傳統(tǒng)方法的有效性和合理性。

60年代起，國外學者已經開始對橋梁結構抖振問題的研究。Davenport最早將概率統(tǒng)計的方法引入到橋梁等細長結構的抖振響應分析中，應用隨機振動理論來分析橋梁抖振響應的方法，開辟了橋梁氣動彈性研究的新領域，并成為至今人們研究抖振問題的主要方法之一。但在這個處理過程中，波動氣動力的空間相關性由來流的空間相關性所代替。考慮自然風場的非定常性，Davenport提出了氣動導納的概念來修正其按準定常氣動力模型計算的誤差。但氣動導納函數包涵了多種影響因素，無法準確體現(xiàn)風速及相應荷載相關性之間的關系。

Larose［2－6]研究作用在橋面板上的陣風作用所造成的風荷載的空間分布。觀測到氣動力的展向相關系數比風速的展向相關系數更大。指出展向氣動導納可能存在一定的缺陷。規(guī)模受限的陣風，作用在大跨度橋梁的橋面板上時，受到扭曲和破壞。在此過程中，渦流展向傳播，增加了展向作用的相關系數。Matsumoto等［7]研究表明鈍體結構表面壓力的展向相關性可能超過風場相關性。Nagao等［8]通過測量兩個不同形狀平板的表面壓力來研究氣動力的空間相關性;研究了波動升力的空間的相關性RL(通過表面壓力積分獲得)與來流空間相關性兩者之間的關系。研究表明作用在再附和分離泡附近的上下表面波動壓力對于振動氣動力的空間相關性起到了重要作用。

趙林等［9]采用改進的互譜導納識別方法，考慮多種影響因素共同作用，識別導納函數分量。劉鑰等［10]利用計算流體力學方法模擬了風場特征，從而得到流場壓力、速度和渦旋分布。

Toriumi［11]指出:通過對日本本四線上兩座橋梁(Honshu-Shikoku Bridges)的自然風的空間相關性研究表明，在低頻范圍內，自然風的空間相關性要比抗風設計規(guī)范中所假定的空間相關性要小。Miyata［12]根據9807和9918兩次臺風期間的明石大橋實橋測量數據進行分析，研究了能量譜和風速振動的空間相關性以及橋面板的響應。兩點空間相關性沒有利用指數公式而是基于各向同性湍流理論利用選擇性相關函數。指數公式中的衰減系數增加幅度隨著距離和風速的增加而較弱。在自然風的相關性較低是否就意味著其荷載效應的相關性較差，其所引起的影響后果如何，就值得去探索。

以上研究，我們認為有必要進行精細化研究，從典型流線型閉口箱梁結構入手，考慮風洞的風場特性制作模型，利用同濟大學二號風洞和高精度壓力掃描閥，來同步測量風速及模型上各測點壓力，通過積分直接得到風荷載，探討了不同湍流度、風攻角、展向距離等參數條件下的風速及其荷載的空間相關性變化規(guī)律。

1 相關性定義

脈動風及其荷載作用的相關程度可以分別利用時域中的相關系數與頻域中的相干函數來描述。

1.1 相關系數

通常在時域中脈動風的相關性一般用相關函數來表示，但自相關函數不能直接了解相關性大小，因此可利用相關系數。對于脈動風速分量來說，以空間兩個不同固定點上的縱向脈動風速在相同時刻的相關性為例，可用互相關系數來表示:

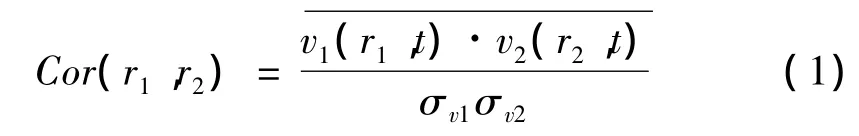
一般情況下，縱向脈動風速的展向相關系數隨著展向間距的增大而逐漸減小，意味著相關性變差。

1.2 相干函數

相干函數又稱為頻率相關系數，是頻率和間距的函數，它描述空間兩點脈動風荷載在頻域上的相關程度，其定義如下式:

式中，SX(r，f)、SY(r，f)分別為隨機過程 X(t)，Y(t)的自功率譜密度，SXY(r，f)為X(t)和Y(t)的互功率譜密度。通過相干函數數值隨頻率變化，來表明兩個隨機變量的相關程度。

Davenport建議的相干函數表達式考慮頻率、兩點間距離及平均風速等因素/f表示波長，因此在陣風脈動中，波長愈長，相關性就愈大。如下式:

式中，建議Cz=7，Cx=8。

Shiotami在試驗基礎上，建議采用只與兩點間距離有關，而與頻率無關的簡單表達式:

式中，建議Lx=50，Lz=60(Lz應大于Lx)。

Krenk認為上述兩式存在兩點缺陷:① 自變量在定義域內取任意值，上述相干函數值恒大于零，這與脈動風是零均值的隨機過程相矛盾;② 對于含頻率項的相干函數，當頻率取零時，不管空間兩點間的距離多大，其值恒等于1，即此時空間兩點的脈動風速完全相關，這與當空間兩點間距離遠大于湍流積分尺度時，兩點間的脈動風速是不相關的通常理解是相互矛盾。

2 試驗模型概況

本次試驗在同濟大學土木工程防災國家重點試驗室TJ－2邊界層風洞中進行。該風洞寬3 m，高2.5 m，長15 m，工作斷面長5 m。模型橫斷面采用流線型閉口箱形橋面板的形式，寬高比采用B/D=12，高度采用30 mm，模型未采用欄桿，風攻角為0°～5°;模型全長為1.7 m。考慮被動風洞的積分尺度及模型局部風壓變化劇烈等因素影響，測壓點間距采用10 mm間距，并在風嘴處每邊設置3個測壓點。將模型與風洞洞壁剛性固定，阻止其在試驗過程中所產生的變形。模型表面由有機玻璃組成。

試驗紊流場的產生主要是利用在模型上游4.2 m處安放三種格柵，從而產生紊流，并控制相應的積分尺度。湍流特性采用熱線儀來測量，采樣頻率為300 Hz。

圖1 模型結構尺寸(單位:mm)Fig.1 Model size(units:mm)

圖2 模型結構橫斷面尺寸(單位:mm)Fig.2 Model Cross Size(units:mm)

圖3 風洞試驗現(xiàn)場Fig.3 Wind tunnel test site

圖4 風嘴局部圖Fig.4 Wind Nozzle Detail

氣動力測量是在模型上展向布置多條測線，間距變化，從2.5 cm～15 cm。每條測線上布置84個測壓點，測點間距考慮風洞的湍流特性，采用1 cm，進行實時測壓。測壓掃描閥采樣頻率為312.5 Hz，采樣兩次，每次采樣時間為40 s。測壓管長度小于100 cm來確保較好頻率的響應。進行表面壓力積分來得到隨時間變化力的相關性數據，包括升力、阻力、扭矩，以及譜分析，并采用多個熱線儀同時刻測量相應風速，然后進行各項相關性研究。

表1 展寬比B/D=12時來流風特性Tab.1 Wind characteristics while B/D=12

3 展向相關性的時域分析

3.1 不同風攻角下的展向相關系數

在時域范圍內利用相關系數研究不同攻角條件下(0°、3°、5°)風速及其荷載效應的展向相關性。試驗對比了湍流度為5%的均勻紊流場8 m/s、12 m/s風速下，阻力間、升力間、扭矩間以及風速的展向相關系數。下圖5分別為當8 m/s、12 m/s風速時各相關系數圖。圖5中DDcor、DLcor、DMcor分別表示兩斷面阻力間、阻力與升力間、阻力與扭矩間的相關系數;MDcor、MLcor、MMcor分別表示兩斷面扭矩與阻力間、扭矩與升力間、扭矩間的相關系數;DD8、LL8、MM8分別表示兩斷面阻力間、升力間、扭矩間在平均風速8 m/s條件下的相關系數;DD12、LL12、MM12分別表示兩斷面阻力間、升力間、扭矩間在平均風速12 m/s條件下的相關系數。在不同攻角條件下，兩不同位置間的升力展向相關系數為0.75～0.79，扭矩展向相關系數為0.65～0.69，均遠遠大于對應位置的風速展向相關系數(0.26～0.42)，這在一定程度上證實了相同時刻不同位置的升力、扭矩的展向相關性遠大于對應位置的風速展向相關性;但阻力的展向相關系數為0.22～0.41，與風速相關系數基本相當。升力相關系數與扭矩相關系數均隨著攻角增加而變化較小，且呈現(xiàn)下降趨勢。而風速相關系數隨著攻角增加也呈現(xiàn)下降趨勢。升力與扭矩間的互相關系數與升力相關系數的變化規(guī)律基本接近，其數值略小于升力相關系數，但比扭矩相關系數大。這在一定程度上體現(xiàn)了相互作用不能忽略。隨著風速的增加，三分力各相關系數均加大，并且升力、扭矩的下降趨勢減小。由此可分析平均風速對于其及相應荷載效應的展向相關性具有一定的影響作用。

圖5 5%均勻紊流場下風速與三分力相關系數Fig.5 Correlation coefficient of wind and aerodynamic forces while turbulence intensity is 5%

3.2 不同紊流度下的展向相關系數

試驗中研究不同紊流度下(5%、10%、15%、20%)三分力與風速的展向相關系數。展向間距為10 cm時，圖6可見升力間、扭矩間、升力與扭矩間的相關系數遠大于風速間相關系數，接近2～3倍;隨著湍流度增加略有增加，但變化幅度較小。其中升力相關系數最大值接近0.9。風速相關系數隨著湍流度增加基本呈現(xiàn)線性增加;阻力相關系數基本與風速規(guī)律一致，而與阻力有關的其它互相關系數在低紊流度時相關系數較小，僅在高湍流度時增幅較大，最大值達到0.45。當湍流度低于10%時，阻力、升力、扭矩間的互相關性較差且變化較小，而當湍流度達到15%時，其相關性增幅較大，表明高湍流度對于阻力的相關性有較強影響，這可能是由于來流湍流積分尺度較小，在經過箱形斷面時被多次撓動，引起二次橫流，從而增強了風速與其效應相關性。

圖6 不同紊流場風速、三分力相關系數(圖例含義同圖5所示)Fig.6 Correlation coefficient of wind and aerodynamic forces under the conditions of different wind velocities

3.3 不同位置的展向相關性分析

試驗研究了5%紊流度下0°攻角條件下，不同位置間風速與三分力的相關系數。通過圖7可見不同位置的風速、阻力、升力、扭矩的相關性隨著展向間距的增大而降低，但風速、阻力的相關系數變化趨勢相同，呈現(xiàn)曲線下降，而升力、扭矩的變化趨勢相同，呈現(xiàn)線性下降，并且升力與扭矩的相關系數遠大于風速與阻力的相關系數。

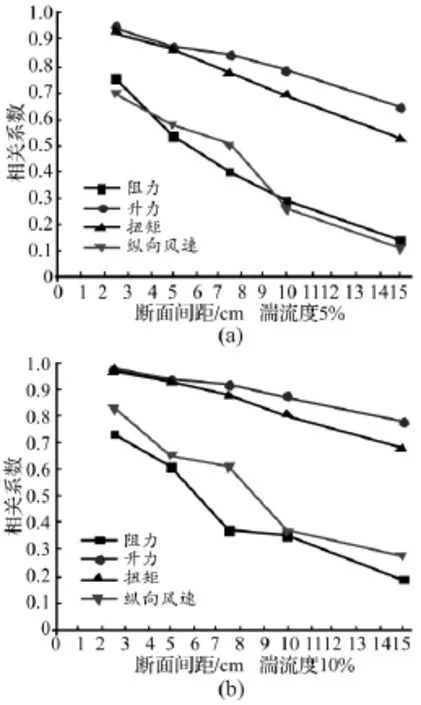
圖7 風速與三分力展向相關系數對比圖Fig.7 Span-wise correlation coefficient of wind and aerodynamic forces under the conditions of different turbulence intensities

4 展向相關性的頻域分析

4.1 不同風攻角下展向相干函數

通過試驗利用頻域上的相干函數來分析風速及其荷載效應的展向相關性。試驗對比了在湍流度下5%均勻紊流場下，分別在8 m/s、12 m/s風速、不同風攻角(0°、3°、5°)時，各位置處的阻力間、升力間、扭矩間以及風速之間的相干函數關系。圖8為當12 m/s風速時各相干函數圖。在不同攻角條件下，相同時刻不同位置的風速與阻力的相干函數在低頻段形式相似，呈現(xiàn)指數衰減，且隨著攻角增加而具有增大的趨勢。但風速相干函數值隨著攻角的變化率略高于阻力，反映了風速相關性并不與阻力相關性完全保持一致。而升力、扭矩的相關函數值隨著攻角增加而變化較小，與折減頻率呈線性變化。這表明在頻域范圍內低頻段時升力、扭矩的相關性遠大于風速、阻力的相關性。

圖8 不同攻角條件下風速與三分力相干函數Fig.8 Span-wise root coherence of wind and aerodynamic forces under the conditions of different attack angles

圖9 不同紊流度下相干函數圖Fig.9 Span-wise root coherence of wind and aerodynamic forces under the conditions of different turbulence intensities

通過時域、頻域的試驗測量結果，可以看出升力、扭矩的展向相關程度遠大于風速、阻力的展向相關程度，且相干函數往往不符合指數衰減規(guī)律，而是接近于線性衰減。當計算抖振響應時采用指數衰減有可能造成響應計算值偏小。

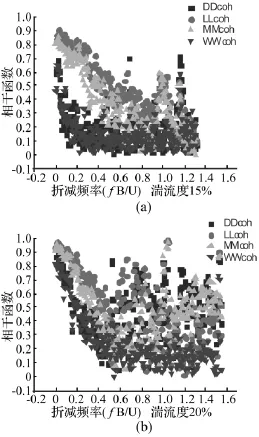
圖10 相同紊流度下相干函數圖Fig.10 Span-wise root coherence of wind and aerodynamic forces under the same conditions of turbulence intensities

4.2 不同紊流度下的展向相干函數

試驗中研究不同紊流度下(5%、10%、15%、20%)兩位置間風速與三分力的相干函數。圖9可見在風洞中風速相干函數隨著折減頻率的增加而呈現(xiàn)指數衰減，但隨著紊流度的增加而增加，且在低頻時表現(xiàn)得比較明顯。分析原因，可能是由于風場的湍流積分尺度小于模型斷面寬度，氣流經過模型表面時存在分離再附現(xiàn)象，從而引起橫流造成展向相關性增加。阻力間相干函數與風速相干函數相似，但升力間、扭矩間相干函數則在不同紊流度條件下，其相干函數值相差較小，隨著折減頻率降低而呈現(xiàn)線性下降。但隨著折減頻率的增加，高紊流度下相干函數反而變大，這可能主要是由于在高頻段產生了自激振動，引起升力、扭矩的相關性增加。通過試驗結果可以看出升力與扭矩的相干函數值隨著折減頻率增加的降幅并沒有比風速與阻力的相干函數值的降幅大。

圖10分別對比在15%、20%紊流度下風速、阻力、升力、扭矩間的相干函數，圖中 DDcoh、lLcoh、MMcoh、WWcoh分別表示兩斷面阻力間、升力間、扭矩間、縱向風速間的相干函數;可見升力、扭矩在相同頻率下，其相干函數值在低頻段明顯高于風速與阻力的相干函數。而高紊流度條件下，風速、升力的相干函數值與升力、扭矩的相干函數值差別逐漸減小。

4.3 均勻流場中不同攻角下風速的相干性分析

試驗研究了均勻流場下不同攻角(0°、3°、5°)條件下，兩位置間風速與三分力的相干函數，發(fā)現(xiàn)不同位置的風速、阻力、升力、扭矩的相干函數在均勻流場條件下隨著攻角變化而均變化較小，這表明來流湍流的特性影響著風速與三分力的相干性，并且可能已超過風攻角對此的影響。均勻流場下，當0°攻角時，風速、阻力、升力、扭矩的相干函數變化基本一致，與前述試驗結果對比，表明紊流度、風攻角與風荷載的展向相關性有密切關系。

5 結論

本文通過同濟大學風洞試驗，利用壓力掃描閥對流線型閉口箱梁斷面的風荷載壓力進行同步測量，了解風荷載的空間分布狀況，比較了來流不同平均風速、湍流度、風攻角、展向間距等參數條件下流線型閉口箱梁斷面的風荷載效應，對風速及其荷載效應的空間相關性進行深入研究，從時域與頻域兩個方面來嘗試分析現(xiàn)象原因，探討其機理及影響因素，可以得出下述主要結論:

(1)通過時域與頻域兩方面研究分析，升力、扭矩的空間展向相關程度要遠大于風速、阻力的相關程度。這表明傳統(tǒng)隨機抖振動氣動力理論存在一定的不足。

(2)在不同風攻角、不同紊流度條件下，風速、阻力的展向相關性規(guī)律近似，其展向相干函數隨著折減頻率增加而呈現(xiàn)指數下降;升力與扭矩的展向相關性規(guī)律近似，其展向相關函數呈現(xiàn)線性下降。

(3)試驗研究表明風荷載的展向相關性與風攻角、紊流度有密切關系。高湍流度可以引起阻力展向相關系數大幅度增加。

(4)風速、阻力、升力、扭矩的相關性隨著展向間距的增大而降低，風速、阻力的相關系數隨著展向間距增加呈現(xiàn)曲線下降，而升力、扭矩則呈現(xiàn)線性下降，且升力、扭矩的相關系數遠大于風速、阻力的相關系數。

本文僅進行了嘗試性研究，存在一定程度的不足，還需要進一步研究，以探索風荷載的空間相關性。

［1] 項海帆，林志興，鮑衛(wèi)剛，等.公路橋梁抗風設計指南［M] .北京:人民交通出版社，1996.

［2] Larose G L，Livesey F M.Performance of streamlined bridge decks in relation to the aerodynamics of a flat plate［J] .Journal of Wind Engineering and Industrial Aerodynamics，1997，69－71(7－10):851－860.

［3] Larose G L，Mann J.Gust loading on streamlined bridge decks［J] .Journal of Fluids and Structures，1998，12(5):511－536.

［4] Larose G L.The spatial distribution of unsteady loading due to gusts on bridge decks［J] .Journal of Wind Engineering and Industrial Aerodynamics，2003，(91):1431 – 1443.

［5] Larose G L，Tanaka H，Gimsing N J，et al. Direct measurements of bu ¤ eting wind forces on bridge decks［J] .Denmark Journal of Wind Engineering and Industrial Aerodynamics，1998，(74 －76):809 －818.

［6] Larose G L.Experimental determination of the aerodynamic admittance of a bridge deck segment［J] .Journal of Fluids and Structures，1999，13(7 －8):1029 －1040.

［7] Matsumoto M，Chen X，Shiraishi N.Buffeting analysis of long span bridge with aerodynamic coupling(Proceedings of 13th National Symp on Wind Engrg［J] .Japan Association for Wind Engineering，1994，227 －232.

［8] Nagaoa F，Utsunomiya H，Noda M，et al.Basic study on spatial correlations of fluctuating lifts acting on plates［J] .Journal of Wind Engineering and Industrial Aerodynamics，2003，91:1349 －1361.

［9] 趙 林，葛耀君，李鵬飛.橋梁斷面氣動導納互譜識別方法注記［J] .振動與沖擊，2010，29(1):81－87.

［10] 劉 鑰，陳政清，張志田.箱梁斷面靜風力系數的CFD數值模擬［J] .振動與沖擊，2010，29(1):133－137.

［11] Toriumi R，Katsuchi H，F(xiàn)uruya N.A study on spatial correlation of natural wind［J] .Journal of Wind Engineering and Industrial Aerodynamics，2000，87:203 －216.

［12] Miyata T， Yamada H， Katsuchi H， et al. Full-scale measurement of Akashi-Kaikyo Bridge during typhoon［J] .J.Wind Eng.Ind.Aerodyn.，2002，90:1517 －1527.