籃球比賽決勝時刻最佳策略的量化與分析

王玉峰，鄭 旗

當代籃球比賽的競技水平發展到了一個前所未有的高度，世界籃球強國之間的競技水平相當接近，高水平籃球隊之間比賽的競爭已日趨白熱化，比賽更加膠著，難分高下。毫厘之差就很可能導致比賽的失利。NBA著名助理教練員戴夫·沃爾曾指出，在 NBA比賽的任何一個賽季，只有不到25%球隊的平均得失分率在六分以上，一支球隊在比賽中有20%～40%勝負只在六分之間甚至更少。可以想象，一支球隊的輸贏往往由上下半場結束前最后幾秒的一個三分球，或在任何一個單節比賽結束前的三個兩分球所決定。就2010-2011賽季NBA季后賽而言，所進行的82場比賽中，比賽結果分差小于六分(含六分)的有29場，分差小于三分(含三分)的有13場。在比賽最后關頭經常出現比分領先的球隊被對手三分絕殺或拖入加時賽情況，這是運氣不好還是策略不佳?在被絕殺之前采用何種策略才能在最后時刻保住微弱優勢以獲取比賽的勝利?采用何種犯規戰術策略更佳?本論文以領先隊領先三分的比賽情境為切入點，利用數學模型量化分析采用常規防守和主動犯規決策時可能出現的情況，并通過實際比賽數據和研究假設進行實例分析。

1 研究對象與方法

1.1 研究對象

本研究以高水平籃球比賽決勝時刻的最后一次攻防策略為研究對象。

1.2 研究方法

1.2.1 文獻資料法 查閱NBA中國官網篩選本研究所需要的技術指標，閱讀有關與籃球比賽決勝時刻、最后時刻戰術策略相關的文獻資料，通過分析與借鑒，為本文所作的假設與論斷提供理論依據。

1.2.2 數理統計法 利用 NBA官網對2010—2011賽季NBA比賽文字直播對部分比賽數據進行統計，并將比賽決勝時刻采用不同的戰術決策所可能出現的情況建立分析模型進行量化分析。

1.2.3 邏輯分析法 將研究結果與比賽中戰術決策的實際運用情況進行比較并進行邏輯分析。

2 數學建模分析的結果與討論

2.1 相關術語的解釋說明與邏輯假設

2.1.1 相關術語的解釋與說明 為比較決勝時刻戰術決策的優劣，在進行討論與分析之前，對論文中將會出現的相關術語作出解釋與說明。

在比賽中各種比賽情境發生的可能性記作為:概率P加該術語英文名稱的簡寫字母。如:進攻方搶得前場籃板球(offensive rebound)的概率記作Por;防守方搶得籃板球(defensive rebound)的概率記作Pdr;三分球(3 points)投中的概率記作P3pt;在激烈對抗下搶投三分球(3 points in desperation)命中的概率記作P3ptd;補籃進球(tip in)(包括補籃和快速投籃)的概率記作Pti;罰球(free throw)罰中的概率記作Pft;球未出手(no shot)的概率記作Pns;打加時賽(overtime)獲勝的概率記作Pot。

2.1.2 相關比賽情境的邏輯假設 雖然比賽中的實際情境比假設更為復雜、多變，但為了簡化分析，論文進行了一些合理的研究假設并接受以上假設成立，即認為各假設情境能夠在比賽中出現，相關假設如下:

(A1)不論落后隊進球還是領先隊搶得防守籃板球，剩余比賽時間都不足以使領先隊完成一次進攻，但夠進攻方完成補籃或一次搶得籃板球后立即出手投籃;(A2)假定落后隊連續兩次搶得籃板球的情況不會出現。此情況發生需要落后隊在比賽中第一次出手投籃不中+搶得前場籃板球+補籃不中+二次搶得籃板球，其概率為P=(1－P3pt)×Por×(1-Pti)×Por，由下1可推算其發生的可能性約為0.001 8，屬于極小概率事件，因此假定該情況不會出現;(A3)在決勝時刻，落后三分的球隊在作最后一投時會選擇投三分球以保證不輸掉比賽，而不是投兩分球;(A4)雙方的犯規次數已經達到了犯規后就罰球的次數，即使領先隊防守時犯規，即使對手沒有做出試投動作，也要罰球;(A5)落后隊在罰球時剩一次罰球機會，但落后多于一分時，則會選擇在第二罰故意將球罰失，然后搶籃板補籃、搶投兩分球或拉到外線投三分(依落后分數而定，剩一次罰球，落后兩分，則搶得前場籃板球后，會直接出手投籃，而不是將球拉到外線投三分球;落后三分的話，會將球將球拉出投三分球);(A6)假設落后隊搶投三分球命中的概率P3ptd為0.2，在領先隊防守下三分球未出手的概率Pns為0.1，搶得前場籃板球后補籃、搶投兩分球成功的概率Pti為0.8，如果雙方進入加時賽，獲勝的概率Pot各為0.5。

2.2 基于邏輯分析與假設下不同戰術決策的勝率分析

2.2.1 領先隊采用常規防守策略下獲勝的可能性分析 針對決勝時刻領先隊采用常規防守所可能出現的比賽情境，大衛·安尼斯曾對其建立了樹狀比賽結果模型進行分析。本文在此基礎上對其分析模型進行簡化與處理，以領先隊是否進行常規防守為切入點，以落后隊的行動結果為分析對象來計算其獲勝的可能性，以箭頭最末端顯示領先隊的比賽結果。綜上所述，領先隊常規防守所可能出現的情況如樹狀見圖1所示:

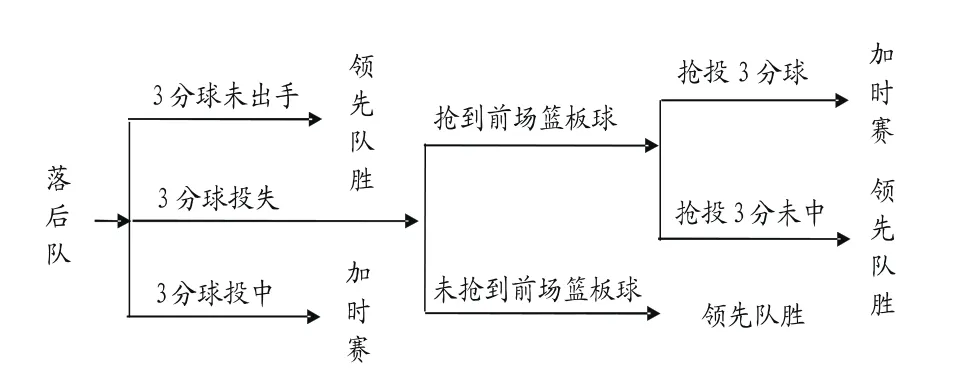
圖1 領先隊采用常規防守策略可能出現的情況

根據圖1可知，在常規防守策略下領先隊獲勝的途徑有:(1)落后隊球未出手，比賽結束，領先隊獲勝;(2)落后隊投中三分球，雙方打加時賽，領先隊在加時賽中獲勝;(3)落后隊投三分球未中籃，搶得前場籃板球，再搶投三分球，雙方打加時賽，領先隊在加時賽中獲勝;(4)落后隊投三分球未中籃，搶得前場籃板球，再搶投三分球仍未中籃，默認領先隊獲勝(比賽時間結束、領先隊獲得后場籃板球或落后隊無出手投三分球的機會或投籃未進等);(5)落后隊三分投失后，未搶得前場籃板球，則領先隊獲勝(此時，落后隊落后三分且失去球權，如果不犯規，時間結束;犯規，領先隊兩罰全進落后五分，二進一落后四分;兩罰全失則落后三分獲得球權，但比賽剩余時間更少，獲勝的可能性更低)。結合以上五種可能，常規防守下領先隊獲勝的可能性用數學公式可表示為:

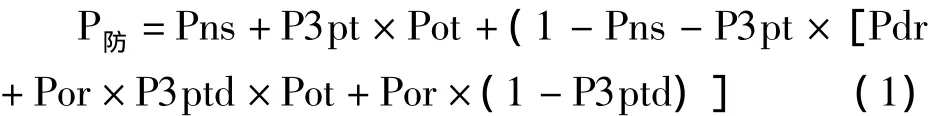
2.2.2 領先隊采用提前主動犯規策略下獲勝可能性的分析 首先需要說明的是領先隊所采用的提前犯規是指在對手出手投籃之前所采用的一般性犯規(非惡意犯規或三分投籃區的犯規)。根據邏輯分析可得知，第一次罰球對可能出現的比賽結果有重要影響，但不論第一罰是罰中還是罰失，第二罰必須要故意罰失。第一罰是否罰進所影響的只是進攻方在第二罰故意罰失之后得分的策略(補籃或者投三分球)，見(A5)。

另外，在比賽中有教練員會擔心故意犯規會有可能使對手在罰中一球后，故意罰失第二球然后搶進攻籃板球，再將球拉到外線搶投三分中籃，在常規賽段就輸掉了比賽。但根據概率分析，此情況發生的可能性為P=Pft×Por×P3ptd，由表1可推算得出其發生概率為屬于小概率事件，所以假設這種可能性不存在。另外臨近比賽結束且比分落后，如果有追平的機會，根據合理邏輯推斷，落后方會抓住一切得分機會追平比賽，而不會冒險去打更復雜、難度更高的三分戰術。另外從概率上進行計算，這也非上等策略，因此排除該策略出現的可能。但如果該情況出現，對于落后隊來說是最好的結果。根據以上推論，同樣借助大衛·安尼斯建立的數學分析模型分析領先隊獲勝的可能性如樹狀見圖2所示:

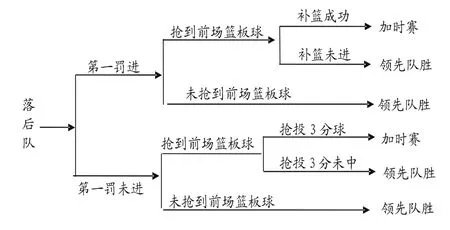
圖2 領先隊采用提前主動犯規策略可能出現的情況

由圖2可得，領先隊主動犯規獲勝的途徑有:(1)落后隊第一罰罰中，第二罰采用罰球戰術，主動將球罰失后搶得前場籃板球，然后成功補籃，最后在加時賽中領先隊獲勝;(2)落后隊第一罰罰中，第二罰主動罰失后搶得前場籃板球，然后補籃未進，領先隊獲勝;(3)落后隊第一罰罰中，第二罰罰失后未搶到前場籃板球，基本確定領先隊獲勝(在這種情況下領先隊領先兩分且擁有球權，如果落后隊不犯規，領先隊勝;采用犯規，兩罰全中領先四分，落后隊翻盤可能性極小;兩罰一中，則領先三分，雙方回到分差原點，但比賽時間更少，對領先隊更有利;領先隊兩罰全失且落后隊最后一攻打成，才有追平或反超的機會，此情況發生的概率極低，因此確定領先隊獲勝);(4)落后隊第一次罰球就將球罰失，然后搶得前場籃板球，再搶投三分球，雙方進入加時賽，在加時賽中領先隊獲勝;(5)落后隊在第一次罰球未進，然后搶得前場籃板球后搶投三分球未進，領先隊獲勝;(6)落后隊第一次罰球將球罰失后未搶得前場籃板球，領先隊獲勝。綜上所述，領先隊獲勝的可能性用數學公式可表示為:

2.2.3 不同戰術決策下比賽結果的量化分析與討論 雖然上述兩個數學公式在理論上得出了領先隊在決勝時刻采用常規防守和提前主動犯規的理論結果與模型，但為了量化推論的結果并利用實戰的概率來檢驗，需要將比賽實際值代入勝率量化公式(1)和(2)計算出在常規防守下P防與提前主動犯規P犯戰術決策的具體值，利用值的大小來量化比較兩種決策下領先隊獲勝的概率。為確保統計分析的真實有效性，本文收集了2010～2011賽季NBA整個季后賽中各指標的統計值，如表1所示。

表1 2010～2011賽季NBA季后賽參賽隊三項技術數據指標統計表

由表 1 可得 Por=0.37，Pdr=0.63，Pft=0.77，P3pt=0.34;結合前文研究假設，將數據代入公式(1)和(2)可得:

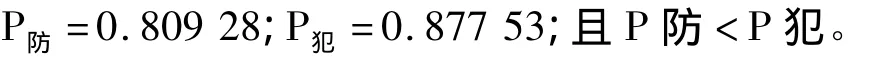
該結果表明:在上述前提下，領先三分但沒有球權的球隊在防守對手作最后一攻時，在對手投三分球之前合理采取主動犯規的策略，是更優策略;由于領先三分且比賽快要結束，采用次優策略獲勝的概率也較高。

結合前人的研究分析與邏輯分析可知，領先隊是否提前采用犯規戰術主要決定于犯規的時機、對手三分球命中率和罰球命中率。由于是否有好的犯規時機是犯規戰術的前提且事先難以預測，而如果領先隊采用的是主動犯規，在很大程度上會選擇對手罰球命中率較低的對手進行犯規，但由于比賽攻防對抗的激烈性與情境變化的不確定性，雖然很難在瞬間做好犯規對象的最優選擇，但在一定程度上具有選擇主動性，唯一不確定的就是對手的三分球命中率，對手在多高的投籃命中率下采用犯規戰術是更佳策略?什么時候采用犯規戰術為次優策略?論文仍以2010～2011賽季NBA比賽季后賽各數據統計值的平均值和假定值作為量化依據，設定對手三分球命中率未知且罰球水平中等(Pft=0.77)，計算領先隊在常規策略下和主動犯規策略下，選擇兩種策略勝率相同(即P防=P犯)時P3pt的值，從而得出在上述前提下，采用提前犯規策略時對手三分球命中率的臨界值。

設定公式(1)的值等于公式(2)的值，根據各統計值和假定值，可得P3pt≈0.2，即在上述前提下，當對手的三分球命中率大于0.2且時機恰當時，采用主動犯規策略在理論上是合理的且獲勝概率相對較高。需要指出的是，上文計算所得值為參考值，不同的球隊、在不同的比賽中有不同的臨界值，在實際比賽中采用犯規策略時對手的三分球命中率一般都應高于此值。

為了便于理解和分析處理，在研究中作出了一些合理的限定和假設，因此默認通過假設所得出的結論可靠的、合理的，對其產生疑問也是合理的。在文中利用模型分析雖然分析較為充分、清晰，理論上得出了兩種決策的戰術可能，但本文仍未對比賽所能產生的可能研究窮盡，應進一步分析到比賽時間終了，但由于在主動犯規對手罰球之后，主動權便掌握在自己手中，只要盡可能地消耗完比賽時間，就可以贏得比賽的勝利，且這一理論在實際比賽中是成立的。不過本文分析結果雖在理論上成立，但在實際比賽中并不排除有特殊情況發生，如領先隊采取主動犯規戰術時，出現技術犯規或違體犯規，綜合筆者所統計的81場以小分差(三分以內，含三分)結束的NBA比賽中，最后24秒出現主動、被動犯規共計114次，判罰結果都為兩次罰球(即一般性犯規)，因此作者在文中未將其列入技術犯規和違體犯規。雖然作者在概率分析中未將其計算在內，但不排除小概率事件出現的可能，如果出現此種情況，對于領先隊將十分不利，因此在運用該戰術時應特別注意犯規的動作與時機的把握，并盡可能地消耗比賽的時間。

綜合實踐考慮，在決勝時刻領先隊選擇主動犯規的情況出現得很少。究其原因可能由于在實際比賽中高強度的攻防對抗與特殊的比賽情境使得防守一方在對手出手之前來不及作出恰如其分的犯規，或擔心被對手造三次罰球的犯規;或者是因為在比賽中落后方在比賽最后時刻主動犯規讓對手罰球，賭對手的罰球命中率并爭取進攻時間已經成為隊員及教練員的一種定勢思維，反其道而行之就難以讓人們接受。但在最后的決勝時刻利用犯規阻止對手投三分球，并通過之間的銜接來消耗掉對手最后的時間，也是一種可供選擇的策略。本案例的另一啟示是在比賽之前要作充分的賽前偵查與準備，清楚地了解對手各個方面的情況，為比賽最后時刻決策作參考依據，從而提高比賽獲勝的概率。從體育戰術學意義講，本研究旨在得到一量化模型，以“從點到面、由此及彼”地尋找戰術活動規律并使研究成果更具科學性。

3 結論

研究分析得出，比賽情境、對手三分球和罰球命中率是決定三分領先的球隊在防守對手作最后一攻時是否主動犯規的核心要素。從理論上講，在合適的比賽時機下，對手三分球命中率達到某一臨界值時，主動對其罰球命中率不高的隊員進行犯規獲勝的概率要高于常規防守，是決勝時刻更佳的戰術決策。但可能由于大多數隊員或教練員在此特殊的比賽情境下擔心對手造三次罰球的犯規、來不及犯規或心理傾向與思維定勢上選擇堅持正常防守，但通過分析結果可知，根據比賽的情境和雙方隊員的特點(如三分球命中率、罰球命中率)，在時機合適時主動犯規增加了贏得比賽的機會，采用此策略并非下策。

［1］ Giorgio Gandolfi.NBA coaches playbook［M］.Champaign，Illinois:Human Kinetics，2009.213 ～225.

［2］ 搜狐—NBA數據中心.賽程結果［EB/OL］.http://data.sports.sohu.com/nba/nba_schedule_by_day.php?d=2011-04-17.

［3］ NBA 中國官網.數據統計［EB/OL］.http://china.nba.com/stats/league/leaders_00.html，2011-12-16.

［4］ David H.Annis.Optimal End-Game Strategy in Basketball［J］.Journal of Quantitative Analysis in Sports，2006:1 ～9.

［5］ 許博.主動犯規戰術理念在籃球比賽中的運用［J］.北京體育大學學報，2009，32(11):114 ～116.

［6］ 畢仲春，潘祥，張勇.當代籃球比賽決勝時刻攻防技戰術結構分析［J］.北京體育大學學報，2009，32(7):105 ～108.

［7］ McCallum Jack.The Last Shot［J］.Sports Illustrated，2008，108(16):38～43.

［8］ 張聚民.第15屆世界男子籃球錦標賽中、外男子籃球隊犯規特征的比較研究［J］.中國體育科技，2007，43(3):98 ～100.

［9］ 姚家新.《孫子兵法》與競技戰術的理論審視［M］.北京:北京體育大學出版社，2010.