二次函數圖像交軸三角形的一個性質

☉河南省商水縣城關鄉一中 康會孌

若二次函數圖像與坐標軸有三個交點，我們把以交點為頂點的三角形叫做二次函數圖像交軸三角形，它有一個有趣性質.

性質 一元二次函數y=ax2+bx+c（ac≠0）的圖像與x軸交于A、B兩點，與y軸交于C點，△=b2-4ac，可得：

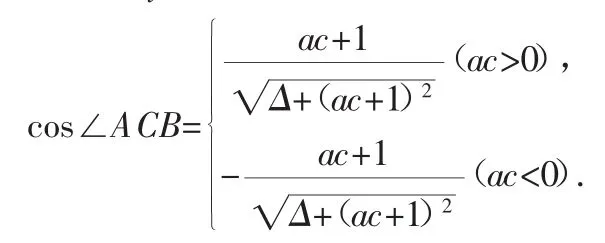
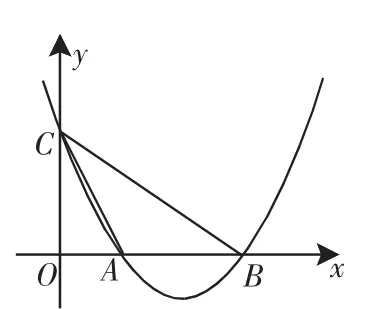
圖1

證明： 如圖1，設A（x1，0）、B（x2，0）、C（0，c），則AC2=x12+c2，BC2=x22+c2，AB2=（x1-x2）2.

性質反映了拋物線內接三角形的幾何特征與二次函數不變量之間的內在聯系，熟悉結論，靈活運用，往往會以簡馭繁，收效奇特.

例1 已知二次函數y=-2x2+x+3與x軸交于A、B，與y軸交于點C.求∠ACB的度數.

解：由函數式知a=-2，b=1，c=3.則△=25，ac=-6＜-1，所以

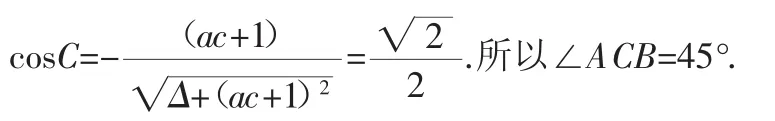
例2 已知二次函數y=mx2+（3-m）x+2m+3與x軸交于A、B兩點，與y軸交于點C，∠ACB為銳角，求m的取值范圍.

解：由函數式得a=m，b=3-m，c=2m+3，所以ac=m（2m+3），△=（3-m）2-4m（2m+3）=（3-7m）（m+3）.

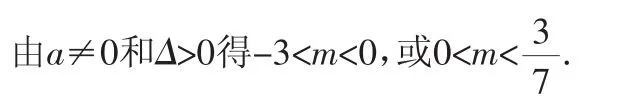
要使∠ACB為銳角，只需ac＜-1，或ac＞0，即m（2m+3）＞0或m（2m+3）＜-1，解之得：

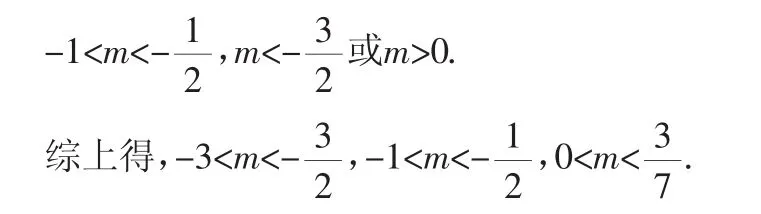
例3 已知二次函數y=mx2-3x+n與坐標軸交于A、B、C三點，且△ABC為直角三角形，若函數圖像經過點，求二次函數的解析式.

解：由△ABC為直角三角形得mn=-1.

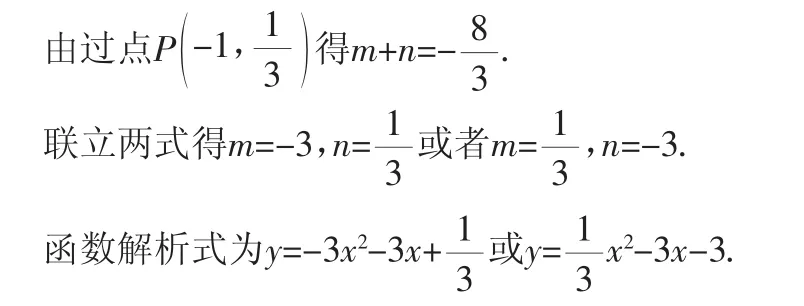
例4 已知二次函數y=ax2-3x+c與x軸正方向交于A、B兩點，與y軸正方向交于點C，經過A、B、C三點作⊙D，若⊙D與y軸相切.（1）求a、c滿足的關系式；（2）求tan∠ACB.

解：設A（x1，0）、B（x2，0）、C（0，c），x1、x2是方程ax2-3x+c=0的兩個正根，則

（2）因為ac=1＞0，△=9-4ac=5，所以∠ACB為銳角