中考數學探究規律題型解法初探

☉江蘇省揚州市江都區實驗初中 姚 凱

近年來，探索規律的題目成為數學中考的一個熱點，目的是考查學生觀察分析及探索的能力.題目一般分為題設和結論兩部分，通常題設部分給出一些數量關系或圖形變換關系，通過觀察分析，要求學生找出這些關系中存在的規律.這種數學題目本身存在一種數學探索的思想，體現了數學思想從特殊到一般的發現規律.是中考的一個難點，越來越引起考生重視.

所謂規律探究型問題，就是根據學生已有的知識基礎和認知特點，分別從直觀形象和抽象符號上進行規律探索，突出數學的生活化，給學生提供更多機會體驗學習和探索的“過程”與“經歷”，使之擁有一定的問題解決、課題研究、社會調查的經驗，使學生經歷探索事物間的數量關系并用字母和代數式表示的過程，建立初步的符號感，發展抽象思維，進一步使學生體會到代數式是刻畫現實世界的有效數學模型.

下面我們根據幾種不同類型的規律變化類型題進行分析.

一、規律探索型問題的分類

1.數列、代數式運算規律猜想型探究題

通常給定一些數字、代數式、等式或不等式，然后猜想其中蘊涵的規律，反映了由特殊到一般的數學方法，考查了學生的分析、歸納、抽象、概括能力.一般解法是先寫出數式的基本結構，然后通過橫比（比較同一等式中不同部分的數量關系）或縱比（比較不同等式間相同位置的數量關系）找出各部分的特征，改寫成要求的格式.

如：有一串單項式：a，2a2，3a3，4a4，…，19a19，20a20，那么第n個單項式是_______.

例1 （2011年湖南益陽，16題）觀察下列算式：

①1×3-22=3-4=-1

②2×4-32=8-9=-1

③3×5-42=15-16=-1

……

（1）請你按以上規律寫出第4個算式.

（2）把這個規律用含字母的式子表示出來.

（3）你認為（2）中所寫出的式子一定成立嗎？并說明理由.

解：（1）4×6－52=24－25=－1.

（2）答案不唯一.如n（n+2）－（n+1）2=－1.

（3）n（n+2）－（n+1）2=n2+2n－（n2+2n+10=n2+2n－n2－2n－1=－1.

猜想歸納是解決這類問題的有效方法，通過對已給出的材料和信息對研究的對象進行觀察、實驗、比較、歸納和分析綜合，作出符合一定規律與事實的推測性想象，從而發現一般規律.它是發現和認識規律的重要手段.平時的教學不能局限于課本，可以設計一些猜想性、類比性的活動，讓學生經歷一個觀察、試驗等活動過程，在活動中通過對大量特殊情形的觀察猜想出一般情形的結論，從而探索事物的內在規律.

2.圖案變化規律探究題

圖案變化規律題是指在一定條件下，探索發現有關圖形所具有的規律性或不變性的問題，它往往給出了一組變化了的圖形或條件，要求學生通過閱讀、觀察、分析、猜想來探索規律，它體現了“特殊到一般”的數學思想方法，考查了學生分析、解決問題的能力，觀察、聯想、歸納的能力，以及探究能力和創新能力，題型可涉及填空、選擇或解答.解決這類圖形規律問題的方法有兩種，一種是數圖形，將圖形轉化成數字規律，再用數字規律的解決問題，一種是通過圖形的直觀性，從圖形中直接尋找規律.

例2 如圖1是某同學在沙灘上用石子擺成的小房子.

圖1

觀察圖形的變化規律，寫出第n個小房子用了_________塊石子.

答案：n（n+4）.

例3 （2011年浙江省，10題）如圖2，下面是按照一定規律畫出的“數形圖”，經觀察可以發現：圖A2比圖A1多出2個“樹枝”，圖A3比圖A2多出4個“樹枝”，圖A4比圖A3多出8個“樹枝”，……，照此規律，圖A6比圖A2多出“樹枝”（ ）.

A.28 B.56 C.60 D.124

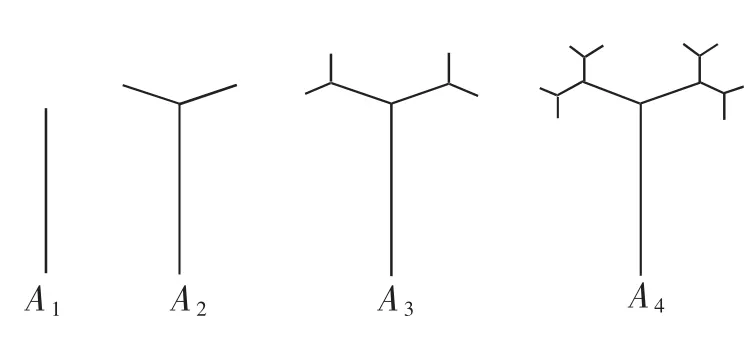
圖2

答案：C.

圖案、圖表具有直觀、形象、簡明，包含的信息量多等特點，解決此類問題需要把“形”轉化為“數”，考查學生數形結合的數學思想.

3.幾何變化規律探究題

觀察幾何圖形，根據題中的變化規律進行分析，猜想下面所沒有給出的圖形變化情況、探究圖形的變化和所求的結果、歸納總結發現規律.

例4 對面積為1的△ABC逐次進行以下操作：第一次操作，分別延長AB、BC、CA至點A1、B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，順次連接A1、B1、C1，得到△A1B1C1，記其面積為S1；第二次操作，分別延長A1B1、B1C1、C1A1至點A2、B2、C2，使得A2B1=2A1B1，B2C1=2B1C1，C2A1=2C1A1，順次連接A2、B2、C2，得到△A2B2C2，記其面積為S2；…；按此規律繼續下去，可得到△A5B5C5，則其面積S5=_____________.

圖3

分析：幾何變化規律探究題往往是根據計算推理、驗證.

如圖3，連接A1C，因為A1B=2AB，根據等高求面積，得到S△A1BC=2S△ABC，

同理S△A1B1C=2S△A1BC，所以S△A1B1B1=6S△ABC，S△C1B1C=6S△ABC，S△A1C1A=6S△ABC.

所以S△A1B1C1=19S△ABC，根據推理運算，不難計算出S5=195=2476099.

二、規律探索型問題常用解法

1.抓住條件中的變與不變

找數學規律的題目，都會涉及到一個或者幾個變化的量.所謂找規律，多數情況下，是指變量的變化規律.所以，抓住了變量，就等于抓住了解決問題的關鍵.而這些變量通常按照一定的順序給出，揭示的規律，常常包含著事物的序列號.

例5 觀察下面兩行數：

2，4 ，8 ，16 ，32，64，..（1）

5，7 ，11 ，19 ，35，67，..（2）

根據你發現的規律，取每行第十個數，求得他們的和.（要求寫出最后的計算結果和詳細解題過程）

解：第一組可以看出是2，第二組可以看出是第一組的每項都加3，即2+3，則第一組第十個數是210=1024，第二組第十個數是210+3得1027，兩項相加得2051.

2.化繁為簡，轉形為數

有些題目看上去很大、圖形很復雜，實際上，關鍵性的內容并不多.對題目做一番認真地分析，去粗取精，取偽存真，把其中主要的、關鍵的內容抽出來，題目的難度就會大幅度降低，問題也就容易解決了.

例6（2011年內蒙古烏蘭察布）將一些半徑相同的小圓按如圖4所示的規律擺放，請仔細觀察，第n個圖形有_________個小圓.（用含n的代數式表示）

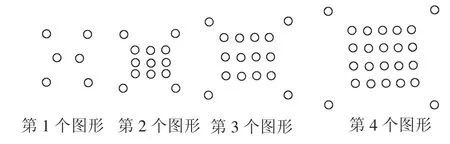
圖4

通過比較，可以發現事物的相同點和不同點，更容易找到事物的變化規律.

3.尋找事物的循環節

有些題目包含著事物的循環規律，找到了事物的循環規律，其他問題就可以迎刃而解.

例7（2011年玉林市中考）“觀察下列球的排列規律（其中●是實心球，○是空心球）：

從第1個球起到第2004個球止，共有實心球________個.

解：這些球，從左到右，按照固定的順序排列，每隔10個球循環一次，循環節是●○○●●○○○○○.每個循環節里有3個實心球.我們只要知道2004包含有多少個循環節，就容易計算出實心球的個數.因為2004÷10=200（余4）.所以，2004個球里有200個循環節，還余4個球.200個循環節里有200×3=600個實心球，剩下的4個球里有2個實心球.所以，一共有602個實心球.

規律探索型問題涉及的基礎知識非常廣泛，題目沒有固定的形式，因此沒有固定的解題方法.它既能充分地考查學生對基礎知識掌握的熟悉程度，又能較好地考查學生的觀察、分析、比較、概括及發散思維的能力及創新意識，因而成為中考的熱點.這就啟發廣大數學教師必須注重過程教學，用科學的方法引導學生親身參與、經歷探索規律的過程，在這樣的過程中讓學生認識數學之美，感受探索的愉悅，逐步培養學生的獨立探究能力.