數(shù)學思想方法照耀下解答疑難問題

☉浙江省寧波市鄞州區(qū)石碶雅戈爾中學 林培娟

不等式是中學數(shù)學的重要組成部分，一元一次不等式則是各類不等式的基礎和起點.含參數(shù)的一元一次不等式（組）試題更是各地競賽的熱門試題.這類試題技巧性強，靈活多變，難度較大，常常影響甚至阻礙學生正常思維的進行.求參數(shù)的值域、定義域等無不貫穿著不等式的求解技巧和方法，經常使用和掌握這些解題技巧，那么含參數(shù)的一元一次不等式（組）難題就會迎刃而解，正如著名數(shù)學家和數(shù)學教育家波利亞：一個想法使用一次是一個技巧，經過多次的使用就可以成為一種方法.一般性數(shù)學方法容易上升為一種思想，如化歸方法常看成是化歸思想，化歸思想是各種問題解決中所體現(xiàn)出的轉化方法的概括［1］.

其實，解決任何問題都需要方法，如果解決眾多不同的問題使用的方法相同，那么這種方法就常被概括為解法思想或思想方法.在數(shù)學思想方法指導下解決數(shù)學問題可以說是達到了數(shù)學解題的最高境界.筆者在浙教版八年級上冊第5章《一元一次不等式》教學過程中，將含參數(shù)的一元一次不等式（組）試題解題實踐分為三類，結合實例，分別剖析以供借鑒.

一、巧用轉化思想，把方程（組）轉化成不等式

轉化思想是解數(shù)學難題的一種重要思維方法，是分析問題和解決問題的基本思想，不少數(shù)學思想都是轉化思想的體現(xiàn).其實數(shù)學中的轉化思想、始終貫穿于整個數(shù)學學習過程之中，它是分析問題、解決問題的有效途徑，它包含了數(shù)學特有的數(shù)、式、形的相互轉換.解含參數(shù)的的方程（組），往往是把參數(shù)當做常數(shù)先解方程（組），然后通過解的取值范圍轉化為參數(shù)不等式.

這是關于x，y的方程組，可以把a當做常數(shù)，通過加減消元法解出用含a的代數(shù)式表示的x，y的值，然后找到關鍵詞“x為正數(shù)”和“y為非負數(shù)”，列出不等式轉化為關于a的不等，式（組）.

這類問題解決可以簡單明了的概括為：

（1）看到關鍵詞，選中不等號；（2）解出方程（組）是關鍵；（3）轉化思想是重點.

練一練：已知關于x的方程3x－m+1=2x－1的解不小于1，則m的取值范圍是_____.

就解題的本質而言，解題既意味著轉化，即把生疏問題轉化為熟悉問題，把抽象問題轉化為具體問題，把復雜問題轉化為簡單問題，把一般問題轉化為特殊問題，把高次問題轉化為低次問題；把未知條件轉化為已知條件；把一個綜合問題轉化為幾個基本問題；把順向思維轉化為逆向思維等.這就是數(shù)學轉化思想，轉化思想能培養(yǎng)學生創(chuàng)新思維能力及邏輯思維能力，可以使學生經歷探索的學習過程，改變學生的學習方式，大大加強學生學習數(shù)學的興趣，最終提高解決問題的能力.因此學生學會轉化思想，有利于實現(xiàn)學習遷移，特別是原理和態(tài)度的遷移，從而可以較快地提高學習質量和數(shù)學能力.轉化的目的是不斷發(fā)現(xiàn)問題，分析問題和最終解決問題.在數(shù)學中，很多問題能化復雜為簡單，化部分為整體，化一般為特殊……

二、合理使用分類討論法，解決參數(shù)系數(shù)問題

分類討論思想是指在解決一個問題時，無法用同一種方法去解決，而需要一個標準將問題劃分成幾個能用不同形式去解決的小問題，將這些小問題一一加以解決，從而使問題得到解決［2］.分類討論思想方法在數(shù)學中非常重要，它對于解決情況復雜的問題往往非常有效，能幫助解題者理清“雜亂無章”的思緒.一元一次不等式中，如果未知數(shù)的系數(shù)含有參數(shù)時，一般都需要對系數(shù)進行討論.

例2 若x>y，且（2－a）x≤（2－a）y，求a的取值范圍.

由不等式的基本性質，兩邊同除一個數(shù)（或式）時要進行分類討論，首先這個數(shù)（或式）不能為零，其次，當這個數(shù)（或式）大于零時，不等式不改變方向，當這個數(shù)（或式）小于零時，不等式要改變方向.所以當系數(shù)2-a的值不確定時，通過對比不等式，不等式的符號改變了方向，對系數(shù)進行分類討論.因為x>y，且（2－a）x≤（2－a）y，所以（2－a）≤0，要考慮小于或等于兩種情況.

練一練：解關于x的不等式ax+2>x+5（其中a為任意實數(shù)）.

化為最簡不等式（a-1）x>3后，左右兩邊同除a-1時，要分類討論：

分類討論是一種邏輯方法，也是一種重要的解題策略，常常能起到簡化問題、解決問題的作用.代數(shù)的解題過程，其實是一個變形過程，往往需要一些條件的限制，從而引起分類討論.分類討論的關鍵問題是對哪個變量進行分類，如何分類.分類時應滿足要求：（1）保證分類對象不重不漏；（2）必須保持同一分類標準；（3）最后必須歸納小結.

三、巧用數(shù)形結合，確定參數(shù)范圍

數(shù)軸是數(shù)與形的一次完美碰撞，數(shù)形結合思想是眾多數(shù)學思想方法中的一種，在教學實踐中，教材中也處處都蘊涵著數(shù)形結合思想.在浙教版的七年級第一章《有理數(shù)》借助于數(shù)軸直接有效地闡述了“相反數(shù)的定義”、“絕對值的意義”、“有理數(shù)大小的比較”等.在已知一元一次不等式組的解集求參數(shù)的取值范圍時，也可巧用數(shù)軸解決問題.

不等式的解集可以在數(shù)軸上表示出來，但這里的m+1和2m-1都是不確定的，所以在數(shù)軸上的位置也不能確定，在數(shù)軸上任意取兩個空心圈（沒有等號時用空心圈表示，有等號時用實心圈表示）作為m+1和2m-1，因為x2m+1，軸上取2m+1的右邊.如圖1，當2m-1在m+1左邊，即2m-1m+1時，不等式組還是無解，所以符合題意的有圖2和圖3，即當2m-1≥m+1時，不等式組無解.

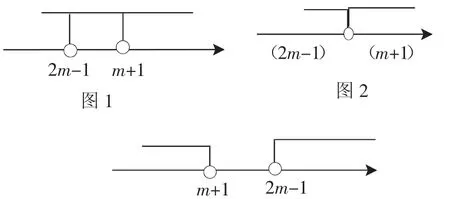
圖3

又如：已知一元一次不等式組整數(shù)解的個數(shù)，求字母m的取值范圍.

例4 已知關于x的不等式mx-2≤0的負整數(shù)解只有-1，-2，則m的取值范圍是_____.

圖4

解一元一次不等式，因為未知數(shù)的系數(shù)為參數(shù)，所以先進行分類討論：（1）m>0時，m有無數(shù)個負整數(shù)解；（2）m=0時，不等式恒成立，x為任何實數(shù)；（3）m<0時要使有兩個負整數(shù)解，從圖4可知

綜上所述，數(shù)形結合的有效運用，使得解題直觀明了，輕而易舉.正如我國著名數(shù)學家華羅庚曾說過：“數(shù)形結合百般好，割裂分家萬事休.”所以在教學過程中，經常提醒學生“得意忘形”不可取.

回顧解題過程我們發(fā)現(xiàn)，含參數(shù)的不等式的成功求解，基于這三種重要思想方法的靈活運用，轉化思想方法、分類思想方法、數(shù)形結合思想方法等，這幾種方法是學習初中、高中甚至大學數(shù)學知識的重要方法.在解題教學中，我們不僅要授學生以魚，更重要的是授之以漁，這是學生學好數(shù)學的最本質的方法.

1.顧泠沅.作為教育任務的數(shù)學思想與方法.

2.張學暉.分類討論思想與數(shù)學解題［J］.新疆石油教育學院學報.1999（4）.