相似三角形等積式問(wèn)題證明“三部曲”

☉廣東省深圳市南山區(qū)第二外國(guó)語(yǔ)學(xué)校 何小波

等積式證明問(wèn)題是初中平面幾何的重要內(nèi)容，它涉及的知識(shí)內(nèi)容廣泛，有利于培養(yǎng)學(xué)生綜合運(yùn)用知識(shí)的能力.等積問(wèn)題綜合性強(qiáng)，類(lèi)型繁多，涉及面廣，難度大，加之許多學(xué)生由于基礎(chǔ)知識(shí)不牢，不善于歸納總結(jié)，結(jié)果在解決等積問(wèn)題時(shí)不能靈活運(yùn)用，感覺(jué)問(wèn)題的分析困難，甚至是無(wú)從下手，望而生畏.為此，筆者總結(jié)提出了等積式問(wèn)題證明的“三步曲”.所謂“三步曲”是指在證明等積問(wèn)題時(shí)，首先考慮把等積問(wèn)題化為等比問(wèn)題，然后證明相關(guān)的三角形相似.其次，在無(wú)法證明三角形相似時(shí)，可用問(wèn)題中所蘊(yùn)含的與等比中某一線(xiàn)段相等的線(xiàn)段或相等的比值來(lái)代替.最后，若無(wú)法找到相應(yīng)的等線(xiàn)段或等比時(shí)則通過(guò)平行線(xiàn)成比例線(xiàn)段這一相關(guān)性質(zhì)找相應(yīng)的比值.下面結(jié)合一些具體的實(shí)例進(jìn)行分析.

1.等積式化比例式，橫找豎找找相似

遇到等積問(wèn)題時(shí)，首先把等積化為等比的形式，然后考慮證明兩個(gè)三角形相似.

例1 如圖1所示，在△ABC中，高線(xiàn)AD、CE交于點(diǎn)O.求證：OC·BD=AB·OD.

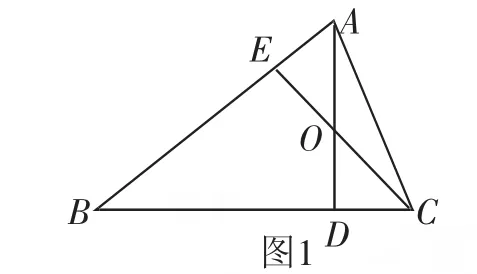
證明：因?yàn)锳D，CE是△ABC的高線(xiàn)，

所以∠EAO+∠AOE=∠DCO+∠COD.

因?yàn)椤螦OE=∠COD，

所以∠EAO=∠DCO.

因?yàn)椤螦DB=∠ODC，

所以△OCD∽△BAD.

評(píng)注：由于比例的性質(zhì)——比例的內(nèi)項(xiàng)或外項(xiàng)可以交換位置，所以在根據(jù)比例式尋找相應(yīng)的相似三角形時(shí)，需橫找或豎找（從比例式的分子線(xiàn)段或分母線(xiàn)段中找相應(yīng)的三角形）.

2.相似若是不好找，等量代換試一試

若在化成比例式后，不能通過(guò)直接找兩個(gè)三角形相似來(lái)實(shí)現(xiàn)等積的證明，此時(shí)可通過(guò)查找問(wèn)題中所隱含的相等的線(xiàn)段或相等比值的條件，用等線(xiàn)段或相等的比值來(lái)代替比例式中的相關(guān)量，再在此基礎(chǔ)上通過(guò)找三角形相似來(lái)證明等積問(wèn)題.

例2 如圖2，?ABCD中，E為邊AD延長(zhǎng)線(xiàn)上的一點(diǎn)，BE交CD于F.試證明：CD·BC=AE·FC.

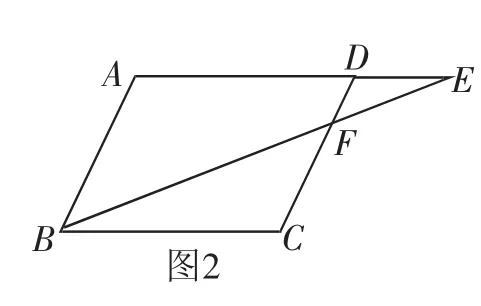
證明：因?yàn)樗倪呅蜛BCD是平行四邊形，

所以∠A=∠C，AB=CD，AD∥BC.

所以∠CBF=∠AEB.

又因?yàn)锳B=CD（已證），

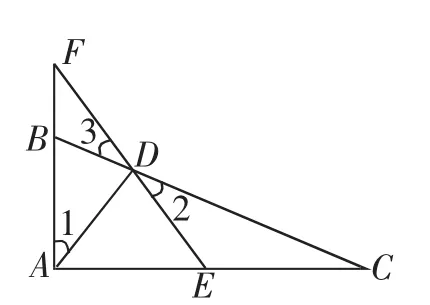
圖3

例3 如圖3，已知在△ABC中，∠BAC=90°，AD⊥BC，E是AC的中點(diǎn)，ED交AB的延長(zhǎng)線(xiàn)于點(diǎn)F.求證：AB·AF=AC·DF.

證明：（略）.

評(píng)注：在證明比例式時(shí)，如果直接證明或等量代換有困難時(shí)，則可以考慮等比代換或等積代換，利用中間比（積）過(guò)渡.

3.平行線(xiàn)段轉(zhuǎn)比例，兩端各自拉關(guān)系

證明等積時(shí)，在無(wú)法證明兩個(gè)三角形相似且又無(wú)法找到問(wèn)題中所蘊(yùn)含的等線(xiàn)或相等的比值時(shí)，可進(jìn)行觀察，看看問(wèn)題中是否含有平行的條件，可借助平行線(xiàn)成比例的有關(guān)性質(zhì)來(lái)查找問(wèn)題所含的相等的比值.

圖4

例4 如圖4，梯形ABCD中，AB∥DC，E是AB的中點(diǎn)，直線(xiàn)DE分別與對(duì)角線(xiàn)AC，直線(xiàn)BC相交于M和N求證：MD·NE=ME·ND.

由圖中無(wú)法直接找到相關(guān)的三角形相似，也沒(méi)有相等的線(xiàn)段.

這時(shí)需要考慮用第三個(gè)比例式來(lái)過(guò)渡搭橋.緊扣條件中的AB∥DC，由平行線(xiàn)分線(xiàn)段成比例定理發(fā)現(xiàn)兩式中唯一不同之處僅在于AE、BE，而已知條件中明確了E是AB的中點(diǎn)，即AE與BE是相等的，從而再借助這一等價(jià)關(guān)系可得進(jìn)而證明

評(píng)注：“等積式化比例式，橫找豎找找相似；相似若是不好找，等量代換試一試；平行線(xiàn)段轉(zhuǎn)比例，兩端各自拉關(guān)系”的解題思路，僅僅是等積問(wèn)題眾多證明思路中的一種.等積問(wèn)題千變?nèi)f化，不同的等積問(wèn)題仍需要進(jìn)行具體的分析，選擇恰當(dāng)?shù)姆椒?相信只要在等積問(wèn)題的證明過(guò)程中不斷摸索，不斷總結(jié)，就能找到一種比較適用的證明方法和證明技巧.