分門別類巧求拋物線的解析式

☉山東省萊西市姜山鎮繞領嶺中學 張俊芝

在學習了二次函數的性質后，我們可將二次函數的解析式的求法，歸納為下面四種類型.

一、一般式法

用一般式y=ax2+bx+c（a≠0），求解拋物線的解析式，只需解決a，b，c三個待定系數即可.這就需要三個條件，方可列出三個方程，組成方程組，才能求解a，b，c，因此，當已知三個獨立條件時，即可用一般式求出此時拋物線的解析式.

例1（海口市中考題）已知二次函數的圖像經過點（-3，2），（2，7），（0，-1），求其解析式.

分析：只需將這三個點的坐標代入解析式，列出以a，b，c為未知數的三元一次方程組.

解：三點代入一般式即可（略）.

點評：用一般式求解拋物線的解析式，需要的三個條件也不一定是三個點的坐標，只要是與a，b，c三個待定系數有關即可.如拋物線的頂點、對稱軸、最值等.

二、頂點式法

拋物線的頂點坐標為（h，k），可設拋物線解析式為y=a（x-h）2+k（a≠0），此時只要再尋求另一個條件，求出a即可用頂點式求解.

例2（濰坊市中考題）已知二次函數圖像如圖1所示，求其解析式.

分析：觀察圖形可以發現拋物線的頂點坐標為（2，-1），且過點（0，3）.

解：設所求拋物線解析式為y=a（x-2）2-1.

將x=0，y=3代入所設的解析式得3=4a-1，解得a=1.

所以所求拋物線解析式為y=（x-2）2-1.

點評：知道拋物線的頂點坐標可用頂點式求解拋物線的解析式.若知道與拋物線的頂點坐標有關的其他條件如對稱軸、最值等，也可用頂點式求解拋物線的解析式.

三、兩根式法

若已知拋物線與x軸的交點坐標或交點的橫坐標，可采用兩根式y=a（x-x1）（x-x2），其中與x軸的交點坐標為（x1，0），（x2，0）.

例3（哈爾濱市中考題）已知二次函數圖像與x軸的交點為（1，0）和（2，0），且過點（3，4），求拋物線的解析式.

分析：由于（1，0）和（2，0）兩點是圖像與x軸的交點，可選用兩根式.

解：依兩根式可設拋物線解析式為y=a（x-1）（x-2）.

再將x=3，y=4代入上式可得4=a（3-1）（3-2）.

解得a=2.

所以所求拋物線的解析式為y=2（x-1）（x-2）.

點評：x=1和x=2其實就是方程a（x-1）（x-2）=0（a≠0）的兩根.

四、三種形式的相互關聯

從以上分析，我們發現：

1.在不同的條件下，能選準恰當的方法，求解拋物線的解析式就顯得較為重要，而方法選擇不準，則求起來顯得煩瑣，而且錯誤率也高.

2.同一道題中，可通過篩選，分析已知條件找出多種不同的求解方法，即一題多解.解決問題的正確途徑不止一個，正是必要的數學思想之一.

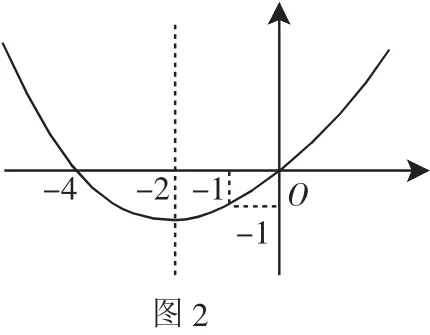
例4 如圖2，已知拋物線的對稱軸為直線x=-2，且過點（-1，-1）和（-4，0），求拋物線的解析式.

分析：本題中既有與拋物線的頂點有關（對稱軸），又有與x軸的交點坐標有關，所以可選用多種方法求解.

解法一：（一般式）設拋物線解析式為y=ax2+bx+c.

依題意得：

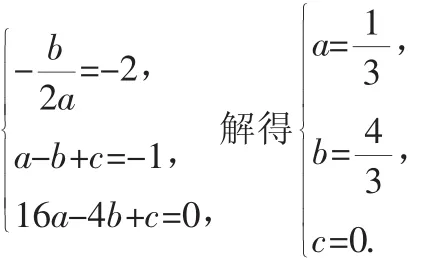
解法二：（頂點式）依題意，拋物線頂點橫坐標為-2，設頂點坐標為（-2，k），則所求解析式為y=a（x+2）2+k.

代入（-1，-1）和（-4，0）可得：

解法三：（兩根式）設A（-4，0），對稱軸與x軸交點為B，拋物線與x軸另一交點為C，由拋物線對稱性可知AC=BC=2，所以C（0，0）.

所以設拋物線解析式為y=ax（x+4）.

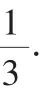
隨著新課程改革的逐步深入，對二次函數部分的考查正逐步降低要求，對二次函數解析式的求解，由于其難度不大，作為對基本技能的考查往往會出現在中考題中，或以填空題、選擇題出現，或作為綜合題的引入問題.熟練掌握這些解題方法是非常必要的.