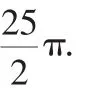“旋轉變換”迷人眼，“見微知著”深追問——2012年浙江義烏市中考第23題的思路突破與反思追問

☉浙江省紹興市建功中學 曹 青

旋轉變換是中考試題必考內容，很多中考卷都用旋轉變換作為壓軸題的命題形式呈現（如2012年浙江義烏卷第23題、北京卷第24題、四川南充卷第21題、四川成都卷第20題、2011年安徽卷第22題等）.突破這類問題需要看清旋轉中心、旋轉前后對應點、對應角、對應邊，排除整個圖形的干擾，善于分離出特殊位置下的圖形（或極限情況）.下面我們結合2012年浙江義烏市中考第23題展開思路分析，并在解后反思中鏈接式展開一系列追問.當然，我們這種努力“指向”“入寶山不空返”（羅增儒語）.

例 （2012年浙江義烏市中考第23題）在銳角△ABC中，AB=4，BC=5，∠ACB=45°，將△ABC繞點B按逆時針方向旋轉，得到△A1BC1.

（1）如圖1，當點C1在線段CA的延長線上時，求∠CC1A1的度數.

（2）如圖2，連AA1，CC1.若△ABA1的面積為4，求△CBC1的面積.

（3）如圖3，點E為線段AB的中點，點P是線段AC上的動點，在△ABC繞點B按逆時針方向旋轉過程中，點P的對應點是點P1，求線段EP1長度的最大值與最小值.

思路突破：

第一步，“特例引路”初感知

可以發現第（1）問中“點C1在線段CA的延長線上”是旋轉后的特殊位置狀態，標注出旋轉前后的對應邊、對應角，有∠A1C1B=∠ACB=45°、BC=BC1，進而得∠AC1B=∠ACB=45°，于是第（1）問獲解.

第二步，發現“相似”快突破

在第（2）問中，考慮到旋轉前后“∠ABC=∠A1BC1”?“∠ABA1=∠CBC1”，再看△ABA1和△CBC1是兩個等腰三角形嗎？能發現這兩個三角形相似嗎？問題不就突破了嗎？要注意面積比等于相似比的平方喲！

第三步，“極限”位置獲最值

初一看，很難理解.讓我們先從邊AC旋轉后掃過的區域思考吧，容易發現當AC邊旋轉到直線AB上時，應該是點P到E的最值位置狀態.此時最大值是點C（P運動到此點處）旋轉到線段AB延長線上，此時最大值PE=7；最小值呢？剛才點P在C處時距離旋轉中心B最遠，想一想點P在AC何處時距離旋轉中心B最短呢？過點B作BD⊥AC于D，此時的點B到直線AC最短距離為BD的長，相應的點P在此處，并旋轉到AB邊上時就獲得最小值了！問題就獲得了貫通.

試題簡答：

（1）由旋轉的性質可得∠A1C1B=∠ACB=45°，BC=BC1.

所以∠CC1B=∠C1CB=45°.

所以∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.

（2）因為△ABCS △A1BC1，所以BA=BA1，BC=BC1，∠ABC=∠A1BC1.

所以∠ABA1=∠CBC1.所以△ABA1S△CBC1.

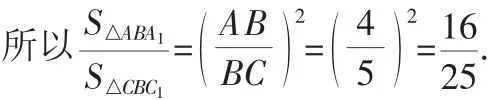
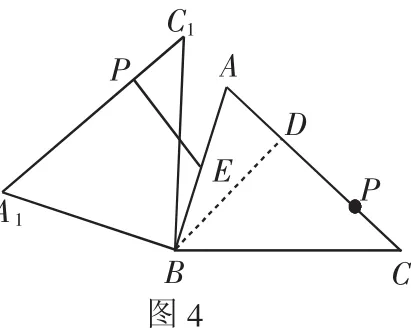
（3）過點B作BD⊥AC，D為垂足.

因為△ABC為銳角三角形，所以點D在線段AC上.

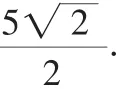
①當P在AC上運動至垂足點D，△ABC繞點B旋轉，

使點P的對應點P1在線段AB上時，EP1最小，

②當P在AC上運動至點C，△ABC繞點B旋轉，使點P的對應點P1在線段AB的延長線上時，EP1最大，最大值為2+5=7.

反思與追問：

決定性的是一步：

在第（3）問中，想到點P分別運動到C點處，并旋轉到AB延長線上時，獲得EP1最大值；進一步發現點P運動到D點處，并旋轉到AB線段上時，獲得EP1最小值.

主要困難在哪兒：

本題的最難點在旋轉后點P到點E的最小值，一般情況容易誤認為是P運動到A點時，當PE=AE=2時為最小值，這種錯誤在于疏忽了點B到直線AC的最小距離其實是垂線段BD的長.

“入寶山不空返”：

作為一道旋轉變換的優秀試題，如果僅滿足于上述求解是不夠的，讓我們鏈接著展開并繼續追問，以便“入寶山不空返”.

鏈接：如圖5，Rt△ABC繞O點逆時針旋轉90°得到Rt△BDE，其中∠ACB=∠E=90°，AC=3，DE=5.則OC的長為（ ）.

講解：根據旋轉的性質，得BC=DE=5，BE=AC=3，則CE=8.根據旋轉的性質可知△COE是等腰直角三角形，計算可得OC=OE=4

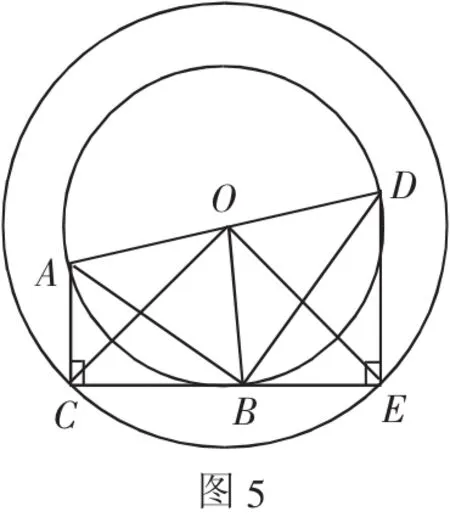
追問1：取OA中點M，P為AC上一動點，若將Rt△ABC繞O點旋轉下去，則旋轉后的P點到M點的距離最大值與最小值是多少呢？

講解：有了最上面的分析，求出AB= 34，在等腰Rt△OAB，發現當P點在A處時，PM有最小值.最大值是點P在C點處時，旋轉到AO的延長線上，此時

現在，我們還想做如下追問：

追問2：我們能否求出邊AC繞點O旋轉360°后掃過的面積？

講解：這是一個圓環，大圓半徑為4即圓環面積為15π.

追問3：怎樣求邊AB繞點O旋轉360°后掃過的面積？

講解：此時大圓的半徑容易發現是，小圓的半徑呢？應該是過O作AB的垂線段，長度是，此時圓環面積為

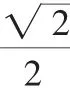
就讓我們給義烏卷第23題增加一個第（4）問（第4次追問）留給讀者自己思考吧！

追問4：邊AC在旋轉過程中掃過的圖形是怎樣的呢？我們能否求出邊AC在旋轉過程中掃過的面積？