物理解題中的遞推方法

楊國平

（紹興市第一中學 浙江 紹興 312000）

當所研究的問題中涉及相關聯的物體較多，并且相互之間的作用有一定規律時，可根據題目特點，從某次具體作用開始，運用歸納、遞推方法，得到一般的表達式（通式）.用遞推法解題的關鍵是導出相鄰兩次遞推關系式.

1 多個研究對象的遞推（歸納）

中學物理常涉及到的多體問題有：按一定規律放置的一系列物體（存在相互作用的物體稱為連接體）、電學元件的網狀連接……對于這類問題，只要找到相鄰兩物體之間力、電流、體積等的分配關系，最后通常能歸納出一個通式.

【例1】有12塊質量分布均勻且相同的積木塊，每塊長度為L，橫截面是邊長為的正方形.將它們在水平面上一塊疊一塊地搭成“單孔橋”，接觸面光滑.要使此橋具有最大的跨度（橋孔底邊的寬度），試計算跨度與橋孔高度之比值.

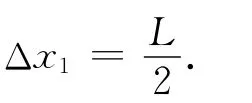
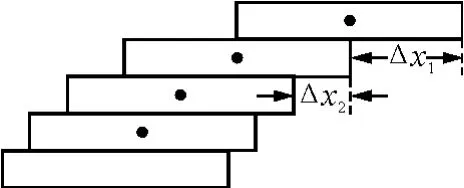
圖1

設第2塊（相對第3塊）的最大伸出量為Δx2，每一積木塊所受的重力均為G.對上面兩木塊，由力矩平衡可得

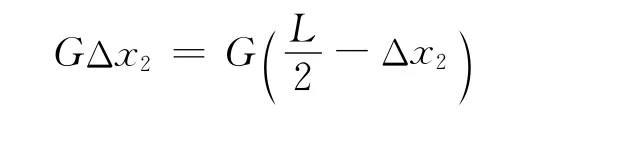
解得

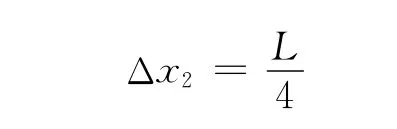
第3塊最大伸出量Δx3滿足

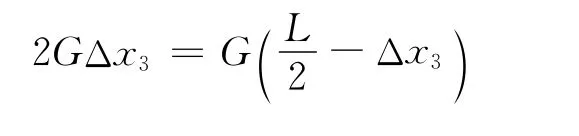
解得

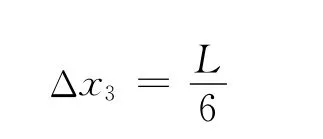
依此類推，最后歸納得出

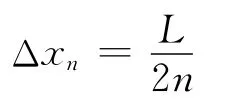
所以總跨度

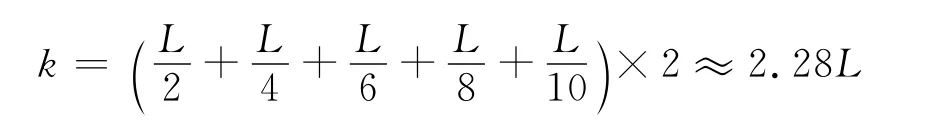
跨度與橋孔高度之比值為

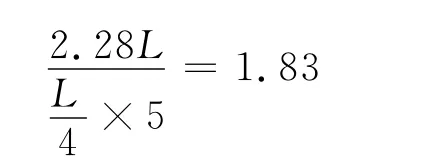
解析：把容器內剩余氣體和抽氣機里的氣體看作一個整體，根據玻 －馬定律，找出每抽氣一次壓強的變化規律，然后歸納遞推出抽n次的壓強表達式.

設初態時氣體的壓強為p0，容器的容積為V，抽氣機的容積為ΔV.每抽一次氣后壓強分別為p1，p2，…，pn，則第1次抽氣后

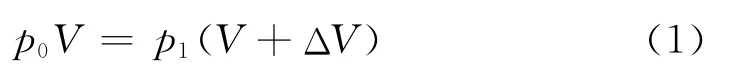
第2次抽氣后

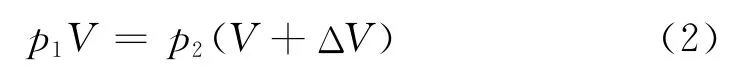
第3次抽氣后

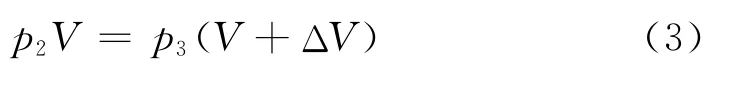
第n次抽氣后

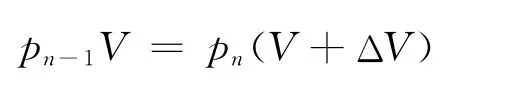
聯立得

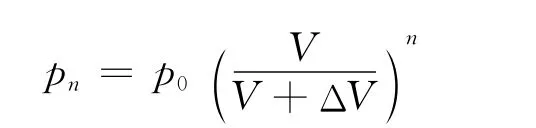
代入數據，得抽氣的次數

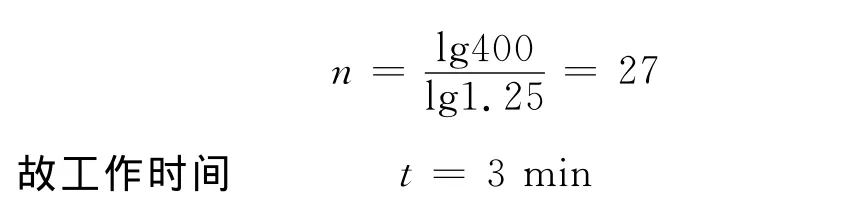
2 多個過程的遞推

最典型的情景莫過于多次碰撞，設法找出前后兩次碰撞中遵循的規律，整個過程（的延續）往往歸結為求等差數列或等比數列之和.這是數理結合的一個典范.

【例3】光滑水平面上固定一V字型槽，兩邊界與夾角α＝3°（圖2中α被夸大了）.一小球從邊的C點＝3m）以速度v＝3m／s、θ＝30°角的方向開始運動，與OA板發生碰撞后又折回與OB板碰撞 ……設所有碰撞都是彈性的.試求：

（1）小球經過幾次碰撞后又回到C點；

（2）此過程所經歷的時間.

圖2

解析：小球在兩板之間的碰撞類似于光的反射.

設小球第1次碰板時的夾角為θ1，如圖3（a）所示，

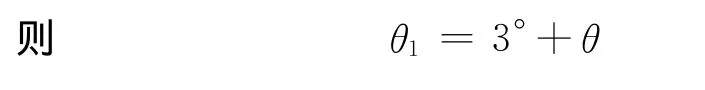
第2次碰板時的夾角

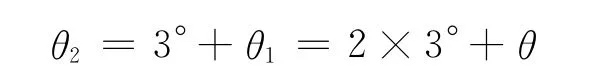
第n次碰板時的夾角

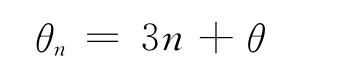
當θn＝90°時小球將沿原路返回，代入數據，有

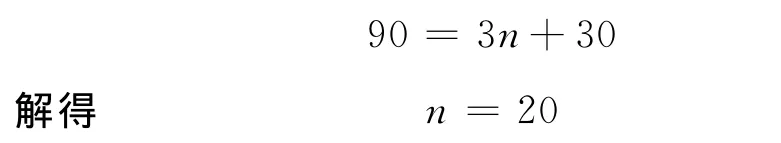
返回C點前共碰了39次.

（2）依次求出兩次碰撞之間的時間，再累加，對本題并不有效，因為尋找兩次運動時間的遞推關系非常困難.可借助光的反射來突破.由鏡像對稱可知，光在兩界面之間的多次反射可等效為鏡面的多次成像，而光的傳播方向不變.由圖3（b）可知，入射點Cn就是離O最近的點，之后往返，總時間

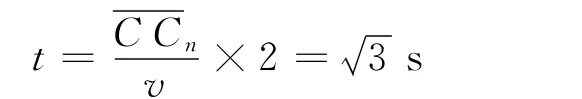
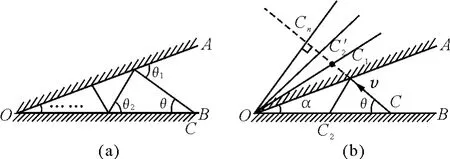
圖3

【例4】一個導體A通過與另一帶電導體B多次接觸來充電，帶電導體B的電荷在每一次接觸后又都被充電到原來的值Q.假定A在第1次接觸后帶電荷量為q.試問采用這種方法A能達到的最大電荷量是多少［1］？

解析：導體接觸必有電勢相等，接觸后帶電荷量應分別與A，B的電容量成正比分配.即第1次接觸后

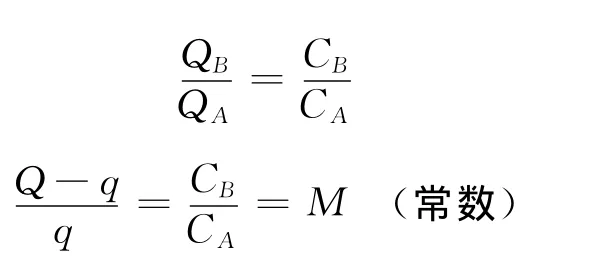
設第2次接觸后A帶電荷量為q2，則

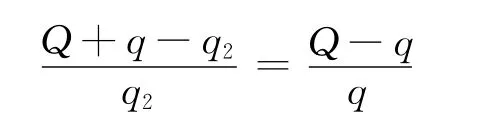
得

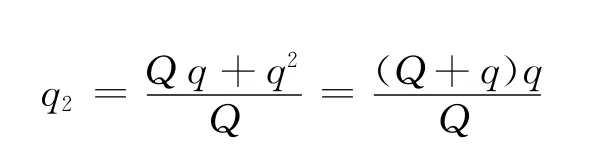
設第3次接觸后A帶電荷量為q3，則

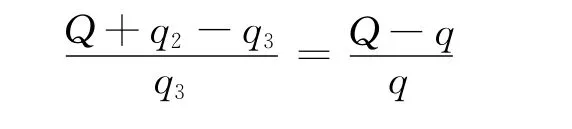
得

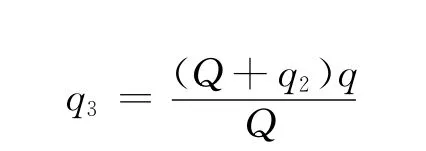
依此類推，第n次接觸后A所帶電荷量qn應滿足

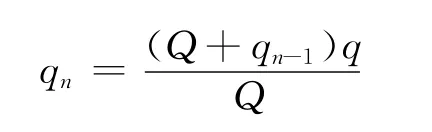
依題意，當多次接觸后A所帶電荷量將達到最大值，即不再改變.故應有qn＝qn－1.則

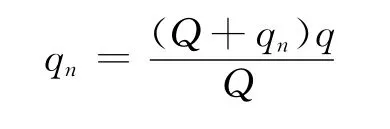
即

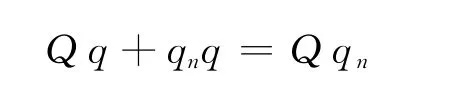
解得

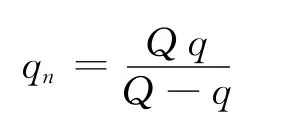
【例5】在一個開有小孔的原不帶電的導體球殼中心O點，有一個點電荷Q，球殼內、外表面是同心球面，半徑分別為a和b.欲將點電荷Q通過小孔緩慢地從O點移到無窮遠，應當做多少功［2］.

解析：當點電荷在球心處，球內外表面分別感應產生等量異號電荷，感應電荷在球心處產生的電勢為

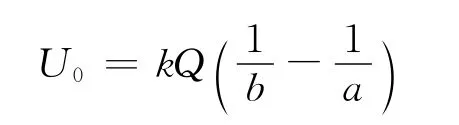
當點電荷Q從球心O點通過小孔移至無窮遠處（電勢為零）時，本題情況下，靜電力做功不能寫成

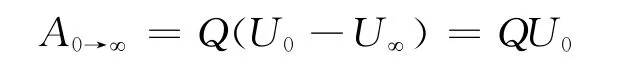
這是因為在移動Q時，O點電勢必然變化，不能用不變的U0與電荷量Q的積QU0表示電場力的功.

那該怎么辦呢？假設從O點通過小孔移出球殼外的電荷是一小份一小份地進行的.每移一小份電荷時，可以近似認為O點電勢不變.再把移動每一小份電荷所做的功加起來，就是所求的總功.

設每次移動的電荷量為q（小量），Q＝nq，即n次移完（n很大）.逐次移q，外力做功分別為

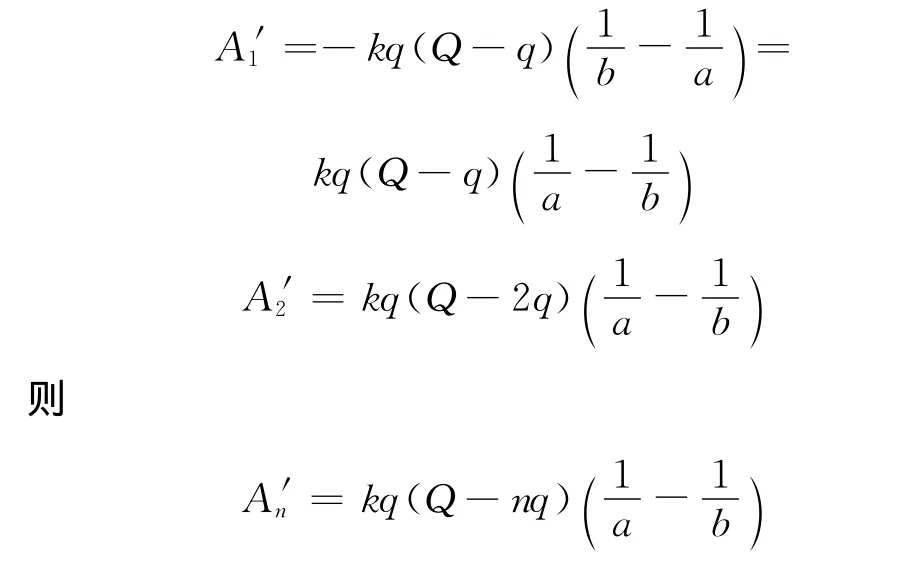
外力做的總功為

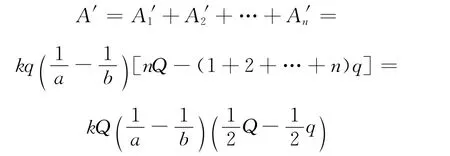
當q→0（即n→!）時，外力總功為

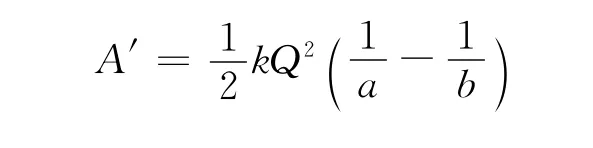
3 多物體多過程遞推

物理問題大多來源于實際生活，對于競賽題尤其如此.這樣不可避免地要面對多個物體，以及多個運動過程.物理學科之難正在于此；然而，這也正是物理學科魅力之所在.

【例6】一塊足夠長的木板放在光滑水平面上，其上放有序號為1，2，3，…，n的相同小木塊，如圖4所示.小木塊質量均為m，長木板質量等于小木塊的總質量.給各小木塊以相應的初速度v0，2v0，3v0，…，nv0，最終所有木塊與長木板以共同速度勻速運動.求：

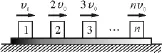
圖4

（1）所有小木塊與長木板一起勻速運動的速度vn；

（2）第1號小木塊與長木板恰好相對靜止時的速度v1；

（3）試推導第k號（k＜n）小木塊與長木板相對靜止時的速度.

解析：（1）由動量守恒知（小木塊與板之間有摩擦）

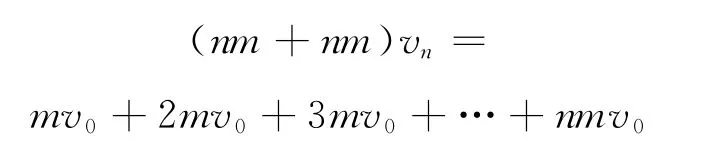
解得

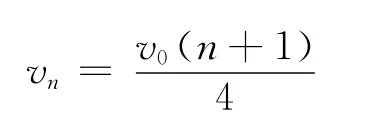
（2）各小木塊做勻減速運動的加速度相同，在相同時間內的速度變化量相同，當1號木塊與長木板的速度都為v1時，2號木塊的速度為v1＋v0，3號木塊的速度為v1＋2v0，依此類推，n號木塊的速度為

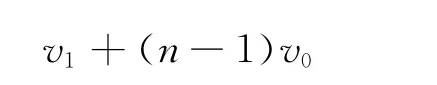
據動量守恒定律有

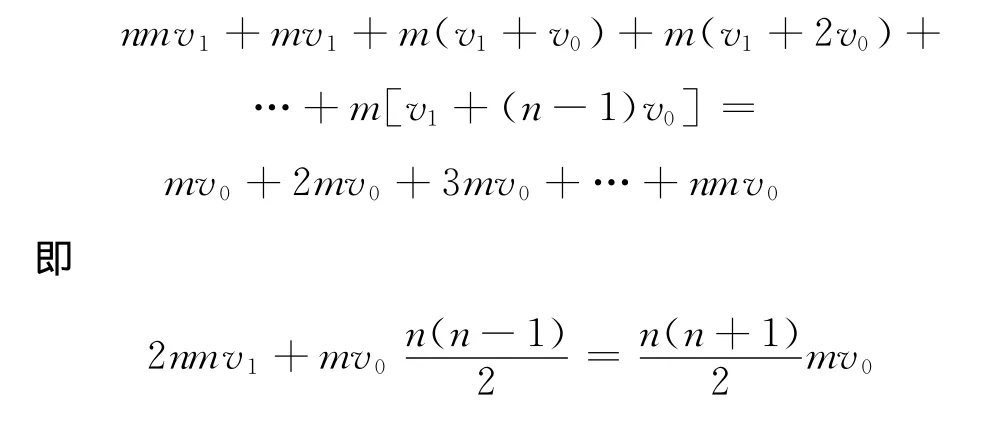
解得

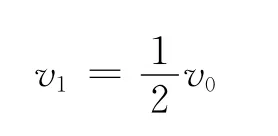
（3）同上，當2號木塊與長木板的速度都為v2時，3號木塊的速度為v2＋v0，4號木塊的速度為v2＋2v0，依此類推，n號木塊的速度為v2＋（n－2）v0，則有

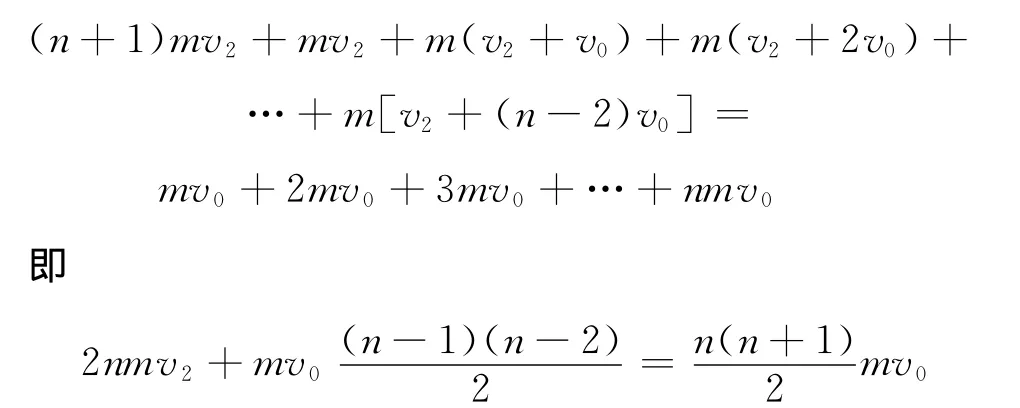
當第k號同速時，有

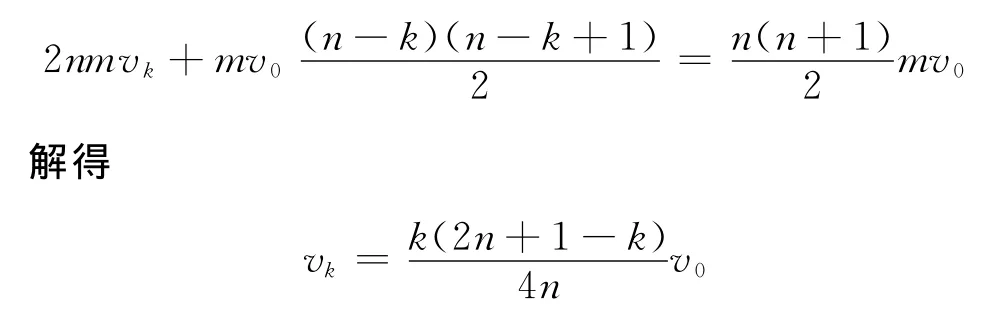
4 警惕遞推“陷阱”

根據題意列出遞推關系式，再用數學歸納法或特殊數列求和等手段，是解決遞推類問題的有效方法.但在某些情況下（尤其是涉及多個過程），不必按過程發生的先后順序遞推，而從初末狀態的全程進行分析，可以起到奇效.在例3的求解過程中已露端倪.眾所周知，對小車滑塊系統，求多次來回后滑塊在車上滑行的相對位移，最好采用能量守恒定律和摩擦生熱的量度式，不要陷入遞推陷阱中.事實上要避免這類陷阱并不容易，請看如下解答.

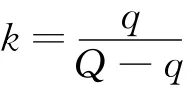
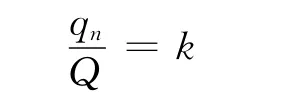
即得

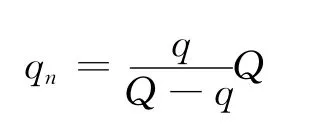
例5方法2：做功的過程伴隨著能量的轉化（此處是靜電場能）.初態時的等效電容量為

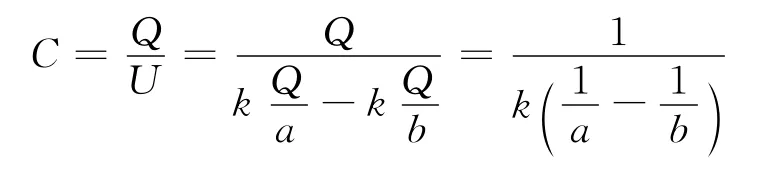
對應的靜電場能

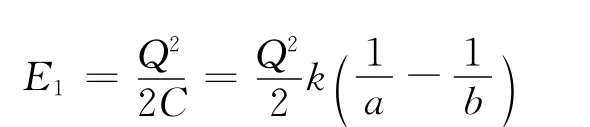
末狀態電容器不再帶電，電場能E2＝0，由功能關系，外力做功W＝ΔE，即得

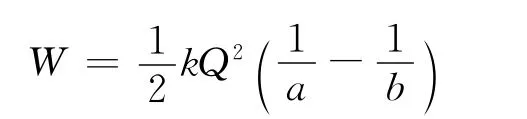
1 谷明杰.高中物理解題思路16講.天津：天津教育出版社 ，2006.7

2 范小輝.新編高中物理奧賽指導.南京：南京師范大學出版社，2005.417