高精度A穩定隱式調諧Taylor級數法在電力系統中的應用

鄭煥坤 常鮮戎 王正輝

（1.華北電力大學電氣與電子工程學院 保定 071003 2.青海省電力設計院 西寧 810008）

1 引言

暫態穩定計算是電力系統基本計算之一。暫態穩定計算方法主要有時域仿真法、直接法和人工智能等方法[1]。時域仿真法作為研究電力系統暫態穩定計算的重要手段，具有直觀、信息量豐富、物理概念清晰等優點，其難點是既要保證算法具有良好的穩定性同時又要具有足夠高精度。1963年Dahlquis引入A穩定性概念的同時也提出了限制性的結果：顯式的線性多步法（包括顯式 Runge-Kutta方法）不可能是A穩定的；A穩定的隱式線性多步法的階數不能超過2，而所有A穩定的2階方法中，梯形公式具有最小的局部截斷誤差常數[2]。自夏道止教授 1983年將高階 Taylor級數法引入暫態穩定計算后[9]，基于Taylor級數的暫態穩定仿真的研究一直沒有中斷。快速高階Taylor級數法是一種較優秀的暫態穩定計算方法，但其數值穩定性較弱[4]。很多學者為了提高其數值穩定性和計算精度做了大量工作，例如引入多步法、隱式方法等。

隱式Taylor級數法較顯式Taylor級數法穩定域明顯擴大[5]。文獻[6]提出了隱式調諧Taylor級數法，并根據經驗試探性地引入調諧參數以改善其穩定。本文在其基礎上通過數學推導，得到具有A穩定性的高精度隱式Taylor級數算法的計算格式。證明了按照本文提出的計算格式設計的隱式高階Taylor級數在具有高計算精度的同時還可以保持良好的穩定性。通過理論推導，證明了該隱式高階Taylor級數法在達到2N階精度時仍然是A穩定的。該方法突破了Dahlquist提出的限制性結果。另外該方法除了適用于電力系統暫態穩定計算也適用于電力系統的中長期仿真計算。

2 隱式Taylor級數法數值計算精度分析

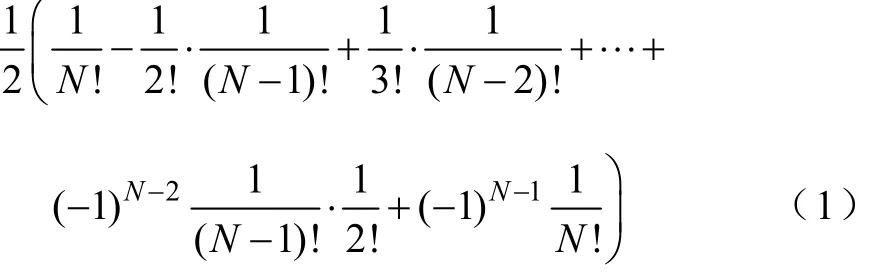
設式（1）=S，當N為偶數時易知S為零。當N為奇數時，有

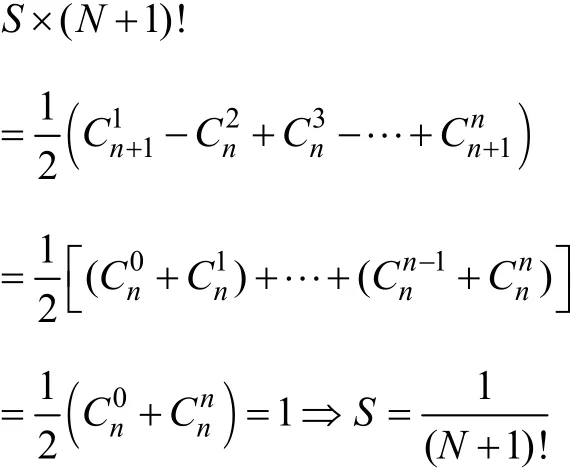
所以當N為奇數時，S=1/(N+1)！

與N+1階奇數情形類似，可證S′=1/K！。

當N為奇數時

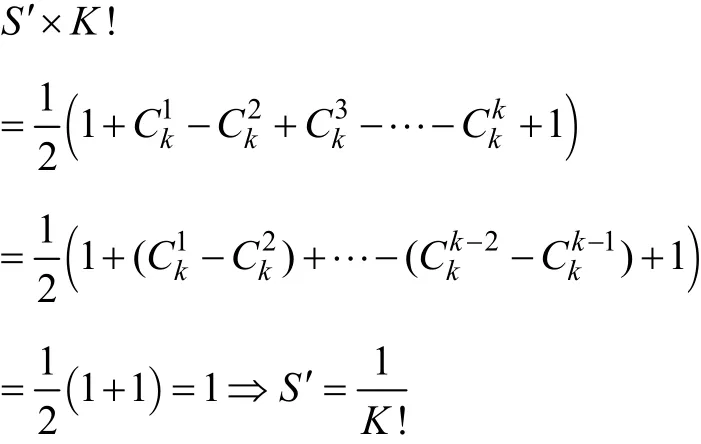
綜上所述，y(1)(x+Δx )的 K階導數的系數為1/K！ (K=1,2,??, N)。經過以上分析后發現，展開階數N與數值精度之間呈如下關系：當N為偶數時精度為N階，而N為奇數時精度為N+1階。

3 隱式Taylor級數法數值穩定性分析

P階展開時改進隱式Taylor級數法絕對穩定域為

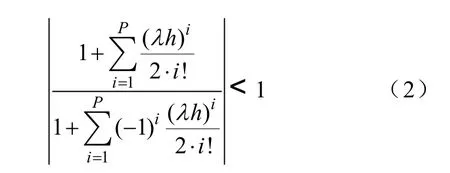
這里λ 為復數。P＝1時，隱式Taylor級數法即等價為A穩定的隱式梯形法。梯形法是二階的方法，也是A穩定的方法中截斷誤差比較小的方法。當P＝1,2,3時，隱式Taylor級數法在hλ 復平面的左半平面。而當P=4時穩定域如圖1中陰影所示。

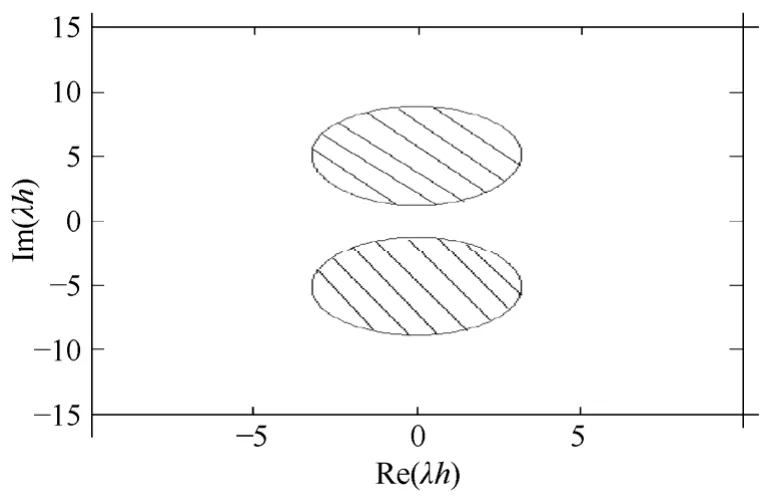
圖1 P=4時隱式Taylor級數法穩定域Fig.1 Stability domain of implicit Taylor series method

隱式Taylor級數法較顯式Taylor級數法穩定域明顯擴大，在相同精度下，絕對穩定域也要比Runge-Kutta法大[5]。由式（2）可知在P＜4時將穩定域的范圍控制在復平面的左半平面即 A穩定區域，當階數升高（P≥4）時，隱式Taylor級數法不再具有如此良好的數值穩定性。

4 隱式調諧Taylor級數法迭代格式

為了使高精度的隱式Taylor級數法具有更強的數值穩定性，引入如下參數調節格式：

式中，ω1, ω2,…,ωn為隱式調諧Taylor級數法調節格式中待定系數。由隱式Taylor級數法迭代格式可知當展開階數為N時，其中各調諧參數需滿足條件：

以上兩式中 ωi(i=1,2 … N)為N階展開時對應于方程組（3）的解。

對應的隱式Taylor級數法絕對穩定域為

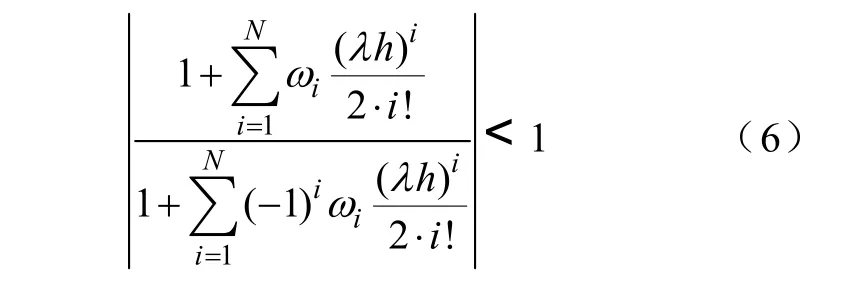
5 隱式調諧Taylor級數法算法穩定性分析

經過參數調節后所得到的上述迭代算法為A穩定的，下面給出證明。以N=4為例，由方程組（3）可知四階展開時隱式 Taylor級數法可達 8階精度（具體證明見調諧隱式 Taylor級數法計算精度分析）。它的穩定域為

式（8）只有當x＜0時才成立，故式（5）的解均在復平面的左邊平面。因此，采用這種調諧方法的隱式Taylor級數法是A穩定的。類似可證N=5,6,??的情形，這里不再贅述。N=5,6階時具體穩定域分別在復平面的左半平面。

6 隱式調諧Taylor級數法計算精度分析

由隱式Taylor級數法數值計算精度分析可知：對于y=f(x)，當N為偶數時精度為N階，而N為奇數時精度為N+1階。對于隱式調諧Taylor級數法，以 N=4為例，由式（3）得到對應參數并與 y=f(x)隱式泰勒級數8階展開式相減，可得（具體化簡過程 從略）： y(1)(x +Δ x)-y(0)(x +Δ x)=O(Δ x9)

可見：隱式調諧Taylor級數法與y=f(x)的8階Taylor展開式相減得到的局部截斷誤差為9O(Δx)。因此當隱式調諧Taylor級數法階數為4時算法精度可達8階。類似可分析其他展開階數的情形。

7 隱式調諧Taylor級數法計算速度分析

在滿足相同計算精度前提下，顯式Taylor級數法的計算速度較常規四階Runge-Kutta法快6倍左右[6]。由隱式調諧Taylor級數法迭代格式，可知若式（4）去掉調諧因子即為顯式高階 Taylor級數法的迭代格式。由式（4）和式（5）可知，對于隱式調諧Taylor級數法每步計算約為顯式Taylor級數法的2倍。由隱式調諧Taylor級數法精度分析可知，當Taylor級數展開N階時其計算精度為2N階。因此，若保持隱式Taylor級數法和顯式Taylor級數法計算精度相同，則相應顯式Taylor級數法必須展開2N階。而顯式Taylor級數法，每一步計算量約為[10]

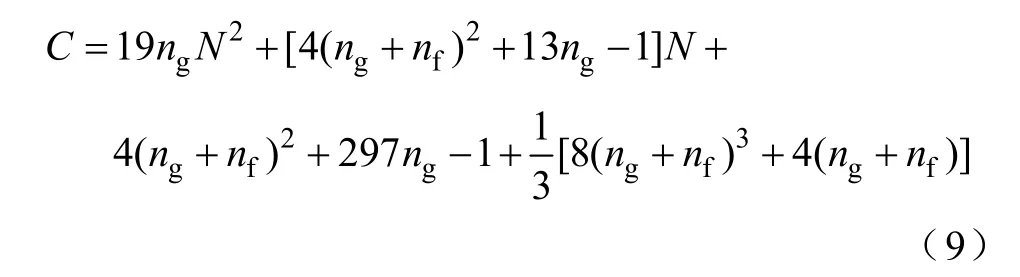
式中，ng為系統發電機個數，nf為故障點個數，N為 Taylor級數展開的階數。由式（9）可知，當顯式Taylor級數法展開階數由N變為2N時增加的計算量還與具體系統規模有關。從本文采用的72機等效系統仿真結果可以看出，隱式調諧Taylor級數至少可以采用2倍于顯式Taylor級數法的步長進行仿真，即進行相同的暫態穩定計算，隱式調諧 Taylor級數法計算步數僅為顯示Taylor級數法的一半。由上述分析可知，隱式調諧Taylor級數仿真速度應略快于顯式Taylor級數法。

仿真時設系統中66號發電機出口母線0s發生三相短路故障，隱式調諧Taylor級數法展開5階，仿真步長0.06s，顯式Taylor級數法展開10階，仿真步長0.03s，進行20s仿真，隱式調諧Taylor級數法實際用時 25.6s，而顯式 Taylor級數法實際用時27.1s。仿真結果驗證了分析的正確性。

8 仿真計算

本文選用我國某省電力系統的等效 72機系統為實驗系統。分別對顯式Taylor級數法、隱式Taylor級數法和隱式調諧Taylor級數法在不同仿真步長下進行計算，并對計算結果進行分析。

8.1 小干擾仿真計算

設系統中14號發電機母線0.5s投入負荷，負荷等值阻抗Z=10+j10，并在6.2s切除該負荷，所有保護均不動作，仿真步長為0.01s，仿真結果如圖2所示。

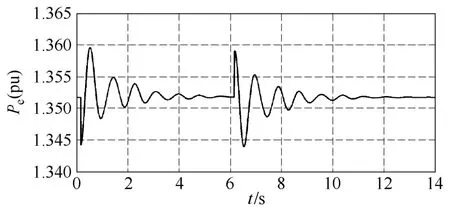
圖2 隱式調諧Taylor級數法小干擾14機Pe曲線Fig.2 The Pe curve of No.14 generator with implicit tuned Taylor method when small disturbance

針對時域數值積分方法對擾動比較敏感的問題，對隱式調諧Taylor級數法進行小干擾仿真。從圖2可以看出，在系統投入小負荷時發生功率振蕩，并在5s時達到新穩定值1.353，切除負荷后最后穩定在未投切負荷時的1.351，未發生局部窗口失真或數值穩定性問題。利用該方法進行了大量小干擾仿真均未發現局部窗口失真或數值穩定性問題。

8.2 系統三相接地故障暫態仿真計算

設系統中66號發電機出口母線0s發生三相短路故障，0.1s故障清除，所有保護均不動作。圖 3為仿真步長為 0.01s時顯式 Taylor級數法、隱式Taylor級數法以及隱式調諧Taylor級數法的仿真曲線。圖4、圖5中仿真步長均為0.03s。圖6和圖7中仿真步長為0.06s。

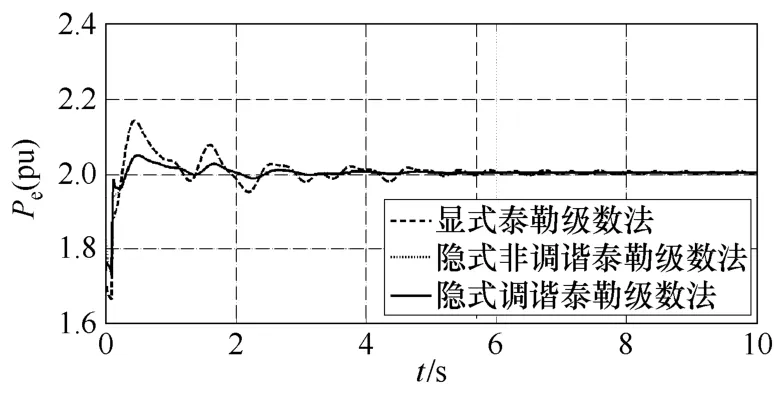
圖3 顯式、隱式和隱式調諧法66號機Pe曲線Fig.3 The Pe curve of No.66 generator with explicit,implicit and implicit tuned method

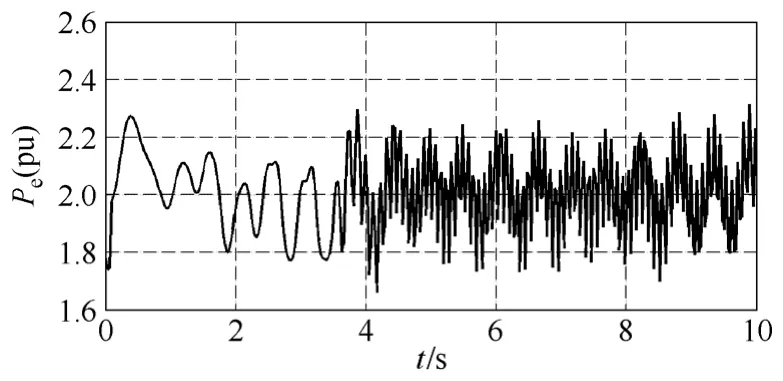
圖4 顯式Taylor級數法66號機Pe曲線Fig.4 The Pe curve of No.66 generator with explicit method

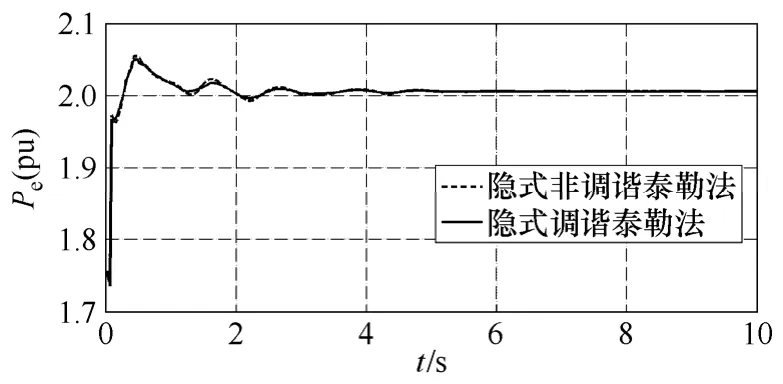
圖5 調諧與非調諧Taylor級數法66號機Pe曲線Fig.5 The Pe curve of No.66 generator with implicit and implicit tuned method

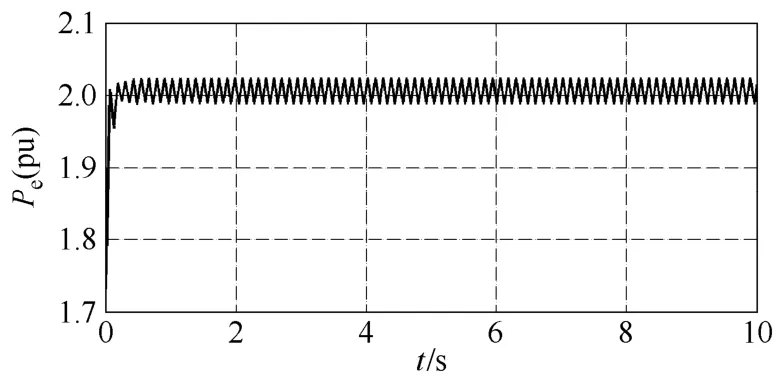
圖6 隱式非調諧Taylor級數法66號機Pe曲線Fig.6 The Pe curve of No.66 generator with implicit method

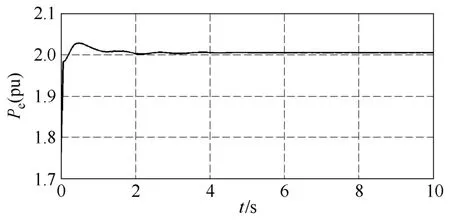
圖7 隱式調諧Taylor級數法66號機Pe曲線Fig.7 The Pe curve of No.66 generator with implicit tuned method

由算例結果可以看出，顯式Taylor級數法的數值穩定性較差，在取小步長時算法是穩定的，而當取較大步長時會出現“誤差淹沒真值”的現象，使計算無法繼續。從圖 3中可以看出，當步長均為0.01s時顯式 Taylor級數法比隱式 Taylor級數法和隱式調諧Taylor級數法振蕩的幅值大，振蕩時間長。當積分步長增長到0.03s時顯式Taylor級數法失去穩定，隱式Taylor級數法和隱式調諧Taylor級數法均能保持穩定；繼續增加步長，當步長為 0.06s時隱式Taylor級數法也失去穩定，而隱式調諧Taylor級數法仍可以維持穩定。從圖5中可以看出在相同步長情況下，隱式調諧Taylor級數法振蕩幅值要小于隱式非調諧Taylor級數法。可見調諧Taylor級數法在保證較高計算精度情況下還具有很大的穩定域。

8.3 系統中長期動態仿真

對系統進行中長期仿真，設系統中243號母線0s投入負荷，負荷等值阻抗為Z=0.3+j0.8，并在30s切除該負荷，所有保護均不動作，仿真步長為0.06s，仿真結果如圖8所示。

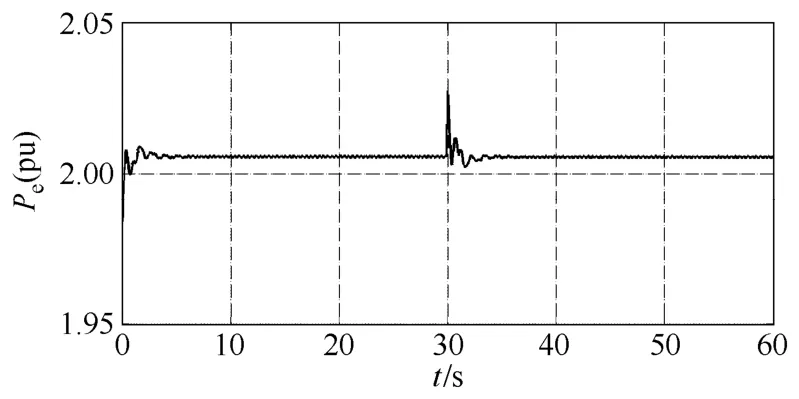
圖8 隱式調諧Taylor級數法66號機Pe曲線Fig.8 The Pe curve of No.66 generator with implicit tuned method

從圖8中可以看出隱式調諧Taylor級數法可以進行大步長、長時間動態仿真，因而可用于中長期的仿真。

9 結論

在隱式Taylor級數法[5]基礎上，引入了隱式調諧 Taylor級數法迭代格式，通過數學推導得出了具有A穩定性的高精度隱式調諧Taylor級數法的計算格式。解決了原隱式算法高精度時數值穩定性較差的問題。當 N=2,3時調諧后即保持了原有的 A穩定性，同時又將穩定精度擴大為 2N階。N≥4時既把穩定域擴大為A穩定同時又將計算精度提高為 2N階。該方法突破了 Dahlquist提出的限制性結果，即隱式高階Taylor級數算法通過調諧以后也可以在高階保持A穩定。另外在仿真中可以使用較大的積分步長，能夠適應較長動態過程仿真計算。

[1]李亦寧.電力系統暫態穩定性評估結果的穩定性研究[D].西安: 西安大學, 2008.

[2]Dahlquist G.A special stability problem for linear multistep method[J].BIT, 1963, 3(1): 27-43.

[3]王守相, 鄭志杰, 王成山.計及不確定性的電力系統時域仿真的區間算法[J].中國電機工程學報,2007, 27(7): 40-44.Wang Shouxiang, Zheng Zhijie, Wang Chengshan.Power system time domain simulation under uncertainty based on interval method[J].Proceedings of the CSEE, 2007, 27(7): 40-44.

[4]郭志忠, 柳焯.快速高階 Taylor級數法暫態穩定計算[J].中國電機工程學報, 1991, 11(3): 7-15.Guo Zhizhong, Liu Zhuo.Fast transient stability simulation by higher order Taylor series expansions[J].Proceedings of the CSEE, 1991, 11(3): 7-15.

[5]袁兆鼎, 費景高, 劉德貴.剛性常微分方程初值問題的數值解法[M].北京: 科學出版社, 1987.

[6]王宇兵, 常鮮戎, 羅艷, 等.基于隱式 Taylor級數法的電力系統暫態計算[J].華北電力大學學報,2005, 32(2): 1-6.Wang Yubin, Chang Xianrong, Luo Yan, et al.An implicit Taylor series method for simulation of power system transient[J].Journal of North China Electric Power University, 2005, 32(2): 1-6.

[7]Furuya S, Iwamoto S.Fast transient stability solution using Taylor expansion and energy function[J].Elect.Eng.in Japan, 1985, 105(3): 123-130.

[8]郭志忠.電力網絡節點解析新探[D].哈爾濱: 哈爾濱工業大學, 1989.

[9]Xia D Z.On-line transient evaluation by system decomposition aggregation and high order derivatives[J].IEEE Transactions on Power Apparatus and Systems, 1983, 102(7): 2038-2046.

[10]白雪峰, 郭志忠.Taylor級數法暫態穩定計算中階數的動態控制[J].電力系統自動化, 1999, 23(22):5-7.Bai Xuefeng, Guo Zhizhong.The dynamic control of oder selection in fast transient stability simulation on by higher order Taylor series expansions[J].Automation of Electric Power Systems, 1999, 23(22): 5-7.

[11]毛安家, 郭志忠, 張學松.一種基于廣域測量系統過程量測數據的快速暫態穩定預估方法[J].中國電機工程學報, 2006, 26(17): 38-43.Mao Anjia, Guo Zhizhong, Zhang Xuesong.A fast transient stability predicting method based on the WAMS process measurement data[J].Proceedings of the CSEE, 2006, 26(17): 38-43.

[12]岳程燕, 周孝信, 李若梅.電力系統電磁暫態實時仿真中并行算法的研究[J].中國電機工程學報,2004, 24(12): 1-6.Yue Chengyan, Zhou Xiaoxin, Li Ruomei.Study of parallel approaches to power system electromagnetic transient real-time simulation[J].Proceedings of the CSEE, 2004, 24(12): 1-6.

[13]房大中, 張堯, 宋文南.泰勒級數在電力系統暫態穩定性分析中的應用[J].天津大學學報, 1998,31(6): 772-777.Fang Dazhong, Zhang Yao, Song Wennan.Application of Taylor series in power system transient stability assessment[J].Journal of Tianjin University,1998, 31(6): 772-777.

[14]于繼來, 郭志忠, 柳焯.基于能量函數高階 Taylor級數展開技術的直接法[J].電網技術, 1995, 19(2):18-20, 24.Yu Jilai, Guo Zhizhong, Liu Zhuo.Direct method with high order taylor series expansions of energy function[J].Power System Technology, 1995, 19(2):18-20, 24.

[15]湯涌.電力系統穩定計算隱式積分交替求解[J].電網技術, 1997, 21(2): 1-3.Tang Yong.An implicit integration alternating solution method for power system dynamic stability simulation[J].Power System Technology, 1997, 21(2):1-3.

[16]Liniger W, Willoughby R A.Efficient integration methods for stiff systems of ordinary differential equations[J].SIAMJ.1970, 7(l): 47-66.

[17]Johnson R B I, Cory B J, Short M J.A tunable integration method for the simulation of power system dynamics[J].IEEE Transactions on Power System,1988, 3(4): 1530-1537.

[18]容文光, 吳政球, 匡文凱, 等.基于泰勒級數展開的N-1牛頓拉夫遜法快速潮流修正計算[J].電網技術, 2007, 31(2): 42-46.Rong Wenguang, Wu Zhengqiu, Kuang Wenkai, et al.Taylor series expansion based N-1 fast power flow revision calculation using Newton-Raphson method[J].Power System Technology, 2007, 31(2): 42-46.

[19]夏世威, 白雪峰, 陳士麟, 等.多群模式 Taylor級數法暫態穩定計算[J].電力系統自動化, 2010,34(10): 24-28.Xia Shiwei, Bai Xuefeng, Chen Shilin, et al.Transient stability calculation by multi-machine equivalent taylor series method[J].Automation of Electric Power Systems, 2010, 34(10): 24-28.

[20]武和雷, 朱淑云, 胡凌燕, 等.適用于工程應用的Taylor展開系數的求解法[J].南昌大學學報(工科版), 2008, 30(2): 175-178.Wu Helei, Zhu Shuyun, Hu Lingyan, et al.Solutions of Taylor expansion coefficients for engineering application[J].Journal of Nanchang University(Engineering & Technology), 2008, 30(2): 175-178.

[21]郭志忠, 朱文東, 柳焯, 等.電力系統暫態穩定的快速時域仿真判定法[J].電工技術學報, 1994, (03):47-49.Guo Zhizhong, Zhu Wendong, Liu Zhuo.Fast judgment of power system transient stability by time domain simulation[J].Transactions of China Electrotechnical Society, 1994, (03): 47-49.

[22]林濟鏗, 李楊春, 羅萍萍, 等.波形松弛法的電力系統暫態穩定性并行仿真計算[J].電工技術學報,2006, 21(12): 47-53, 65.Lin Jikeng, Li Yangchun, Luo Pingping, et al.Parallel calculation for power system transient stability based on waveform relaxation method[J].Transactions of China Electrotechnical Society, 2006, 21(12): 47-53,65.

[23]盧錦玲, 朱永利, 趙洪山, 等.提升型貝葉斯分類器在電力系統暫態穩定評估中的應用[J].電工技術學報, 2009, 24(5): 177-182.Lu Jinling, Zhu Yongli, Zhao Hongshan, et al.Power system transient stability assessment based on boosting bayesian classifier[J].Transactions of China Electrotechnical Society, 2009, 24(5): 177-182.

[24]王守相, 張建軍.基于統計學習的模糊暫態穩定事故篩選與排序[J].電工技術學報, 2006, 21(3): 112-117.Wang Shouxiang, Zhang Jianjun.Fuzzy contingency filtering and ranking of power system transient stability based on statistical learning[J].Transactions of China Electrotechnical Society, 2006, 21(3):112-117.

[25]李琰, 周孝信, 周京陽, 等.基于引入虛擬負荷的發電機暫態穩定預測[J].電工技術學報, 2008,23(3): 103-107, 130.Li Yan, Zhou Xiaoxin, Zhou Jingyang, et al.The generator transient stability prediction based on additional virtual loads[J].Transactions of China Electrotechnical Society, 2008, 23(3): 103-107, 130.