混合粒子群算法在PSS參數優化中的應用

侯莉

(蘭州交通大學自動化與電氣工程學院，甘肅 蘭州 730070)

1 引言

隨著電網規模的不斷擴大，機組單機容量的增加，以及快速勵磁系統的投入，直接導致了系統阻尼的減弱，從而引發了系統低頻振蕩的產生，嚴重影響了系統的穩定運行［1］。為提高系統阻尼，需要在發電機側加裝電力系統穩定器(Power System Stabilizer，PSS)。其原理是通過附加勵磁控制提供所需要的附加阻尼來改善系統的阻尼，增強系統的穩定性［2］。目前，國內外學者在電力系統穩定器參數優化方面做了一定的工作，并提出一些有效的方法對PSS參數進行優化如遺傳算法、人工魚群算法、粒子群算法等［3-5］，但都存在可操作性差、收斂性差、容易陷入局部極值等缺點。本文將使用引入遺傳算法(GA)中的交叉操作的混合PSO，實踐證明這種混合PSO具有更快的收斂速度，更好的全局收斂能力。本文將混合PSO用于PSS參數優化設計，并進行仿真，實例證明了該算法優化PSS的有效性和優越性。

2 粒子群算法

2.1 PSO的基本原理

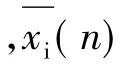
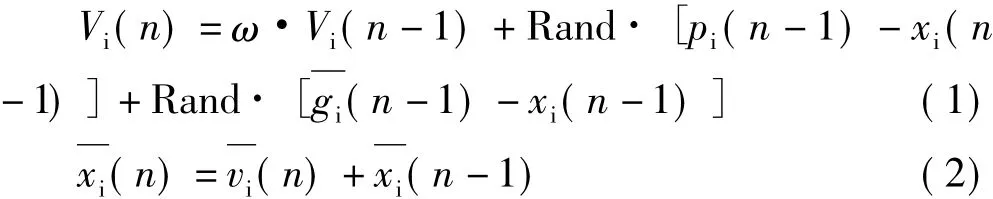
式中:ω為慣性權值;Rand為在［0，1］范圍內變化的隨機數;n為迭代次數;粒子數i=1，2，…，s。

2.2 混合粒子群優化算法(HPSO)

Lovbjerg，Rasmussen和Krink于2000年提出將遺傳算法中的交叉操作也引入PSO的HPSO模型。交叉型PSO在粒子群進行速度和位置的更新后，以一定的交叉概率從所有粒子中隨機選擇待交叉的粒子，然后兩兩隨機組合進行交叉操作產生后代粒子，取代雙親粒子。后代粒子的位置和速度矢量如下所示:

交叉操作使后代粒子繼承了雙親粒子的優點，在理論上加強了對粒子間區域的搜索能力。實驗證明，引入交叉操作的HPSO對于多峰函數，不僅加快了收斂速度，而且找到了更好的解。

3 PSS的設計

3.1 PSS的模型

本文PSS采用超前-滯后校正模型，以發電機的轉速偏差Δω為輸入信號，其傳遞函數如下:

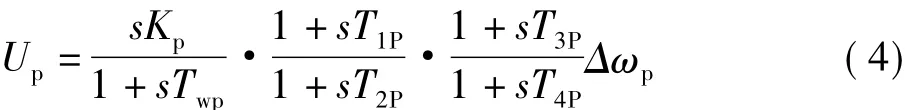
式中:Up為第p臺發電機的PSS輸出信號;Twp為隔直環節的時間常數;T1P、T2P、T3P、T4P為超前 -滯后環節的時間常數;Kp為PSS增益與隔直環節時間常數的乘積。

3.2 PSS的優化目標

在PSS參數優化時必須兼顧兩方面的要求，那就是PSS應該既能夠盡可能高效地阻尼小擾動引起的振蕩，又能在整個頻段上都有效地發揮其阻尼低頻振蕩的作用［7］。PSS能否在整個頻段有效阻尼低頻振蕩取決于PSS的頻率響應特性，即其超前-滯后環節參數。因此，本文擬對PSS超前-滯后環節進行參數。

以整個低頻振蕩頻段(0.1～2Hz)上PSS產生的附加勵磁轉矩ΔTe與Δω相位最大限度接近為目標進行優化，選取目標函數為:

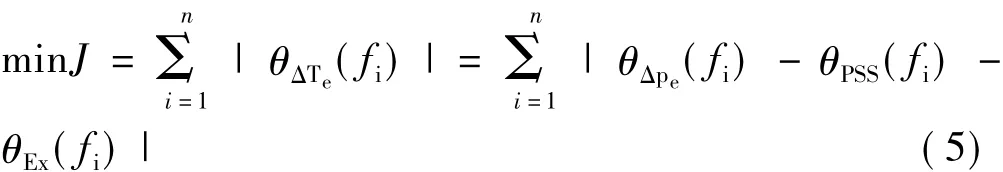
式中:f1，f2，…，fn，是等比數列，代表低頻振蕩頻段上n個頻率點，f1=0.1Hz，fn=2.0Hz，它們是一個等比數列。θΔPe(fi)、θPSS(fi)、θEx(fi)、θΔTe(fi)分別表示f=fi時ΔPe相對Δω的超前角、電力系統穩定器滯后角、勵磁系統滯后角、ΔTe相對Δω的超前角。當n足夠大時，以J最小為目標進行優化即可實現在整個頻段上ΔTe與Δω相位最大限度接近，約束條件為θΔTe(fi)?(-45°，10°)。

4 HPSO優化PSS參數

優化算法的流程如下:

Step1:初始化。

Step2:更新粒子適應度值，利用式(5)求出目標函數值J，將該粒子的適應值更新為1/J，如果存在某個θΔTe(fi)越限將其適應值減去一個懲罰值。

Step3:比較每個粒子的適應值和當前個體最優解pbest適應值，若對于某個粒子而言其適應值大于pbest適應值則將當前位置作為該粒子個體最優解pbest;將gbest設為所有粒子pbest中適應值最大的pbest。

Step4:用式(1)、(2)更新每個粒子的位置Xi，速度Vi，如果Xi，Vi的某維越上限或下限，將其設定為該維上限或下限值。

Step5:按交叉概率從粒子群中選出待交叉粒子，兩兩隨機組合進行交叉操作產生后代粒子，取代雙親粒子，后代粒子按式(4)生成新粒子的初始速度和位置，其pbest設為初始位置。

Step6:如果 iter＜50，iter=iter+1，轉至步驟2。

Step8:輸出優化結果。

5 PSS參數優化與仿真結果

為了驗證算法性能及其對PSS參數優化效果，本文在Matlab7.0仿真環境下［8］，基于IEEE四機兩區域系統進行仿真。

圖1 四機兩區電力系統結構圖

Kundur四機兩區系統結構如圖1所示，發電機G1、G2、G3、G4采用五階模型，其額定容量均為 900 MVA，并且均配有自并勵靜止勵磁系統［9］。根據參與因子選址方法將PSS加裝在G2，G3兩臺發電機上。

圖2、圖3為小擾動下發電機G2、G3的Δω-t和ΔPe-t仿真曲線，由仿真結果可見，HPSO優化后的PSS使得系統振蕩幅值較小，且可以使系統在小擾動下較快恢復穩定，其優化的PSS相較基本PSO優化的PSS具有更好的阻尼發電機電磁功率和角速度振蕩的作用。

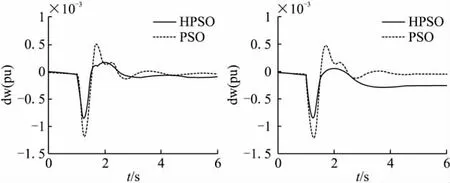
圖2 發電機G2、G3Δω-t仿真曲線

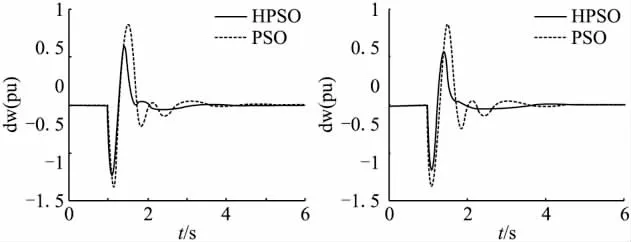
圖3 發電機G2、G3ΔPe-t仿真曲線

6 結論

本文將引入交叉操作的粒子融合算法用于PSS參數的優化，并基于四機兩區域系統對其進行仿真分析，驗證了采用HPSO算法優化后的PSS可以更好的阻尼低頻振蕩，提高系統的穩定性。

［1］劉楊名.電力系統穩定器(PSS)參數優化整定的研究［D］.上海：上海交通大學，2007.

［2］王惠忠，鄧科，鄭偉.抑制電力系統低頻振蕩綜述［J］.工業儀表與自動化裝置，2009，1：15-20.

［3］M.A.Abido.Optimal Design of Power-System Stabilizers Using Particle Swarm Optimization.IEEE Transactions on Energy Conversion，2002，17(3)：106-113.

［4］王德意，閻偉，邱景東，等.基于遺傳算法的電力系統穩定器參數優化［J］.電力系統及其自動化報，2006，18(3)：59-63.

［5］胡曉波，陳中，楊海風，等.其于人工魚群算法的PSS參數優化［J］.電力系統自動化設備，2009，29(2)：47-49.

［6］紀震，廖惠連，吳青華.粒子群算法及應用［M］.北京：科學出版社，2009.

［7］郭強.電力系統穩定器整定方法的仿真研究［J］.華北電力，2009，37(1)：135-140.

［8］李維波.MATLAB在電氣工程中的應用［M］.北京：中國電力出版物，2007.

［9］Abido，M.A.Optimal Design of Power System Stabilizers Using Particle Swarm Optimization.IEEE Power Engineering Review，2009.