基于MATLAB的天生橋二級電站PSS仿真分析

朱建偉

(南方電網調峰調頻發電公司天生橋水力發電總廠，貴州 興義 562400)

1 前言

隨著電力系統規模不斷擴大，大區之間聯網，以及采用高增益的勵磁調節器來改善發電機電壓精度及系統穩定性，使得低頻振蕩的現象時有出現，威脅系統的正常運行。目前，電力系統普遍采用在勵磁調節器上附加電力系統穩定器(PSS)的附加勵磁控制方案，引入功率增量、轉子角增量、角速度增量或它們之間組合的反饋作用，能有效地增強發電機勵磁系統的阻尼，抑制低頻振蕩的發生，從而改善電力系統的穩定性。

目前針對PSS的研究，主要集中在參數辨識［1］及參數優化［2］，抑制低頻振蕩機理分析［3］，及系統的建模和仿真［4］等方面。在眾多的電力系統仿真工具中，Matlab中SPS模塊以其使用簡易和界面友好而被越來越多的電力工作者采用。SPS擁有豐富的電機、負荷、電源、測量及電力驅動的專用元件，其模塊化的設計功能和圖像化的建模環境給使用者帶來極大的便利。本文首先用轉矩向量分析法分析了低頻振蕩產生的機理和PSS對低頻振蕩的抑制，然后以天生橋二級電站#1機組為例，建立基于Matlab的單機無窮大系統模型，最后通過仿真實驗證明PSS對低頻振蕩的抑制作用。

2 PSS對低頻振蕩的抑制

De Mello等運用阻尼轉矩的概念對單機無窮大系統低頻振蕩的現象進行了探討和分析，指出電力系統中產生持續等幅的或者增幅性的低頻震蕩，其根本原因是由于系統中產生了負阻尼抵消了系統原有的正阻尼，使系統的阻尼變的很小甚至為負值［5］。

2.1 低頻振蕩產生原因

在同步發電機的數學模型中，δ表示功角，ΔUt表示機端電壓偏差，它有兩個分量 ΔUt1和 ΔUt2，其中ΔUt1=K5Δδ，K5為比例系數。ΔMS表同步轉矩系數，ΔMS表示阻尼轉矩系數。當負荷較重時，δ角較大，K5＜0，ΔMS＞0，電壓調節器能夠增加系統的同步能力。但ΔMD＜0，即電壓調節器加入后，總的阻尼轉矩系數減小，隨著電壓放大系數的增加，當總的阻尼轉矩系數為負時，阻尼轉矩將助長Δδ的上下變化，機組將發性振蕩失步。

若系統處于平衡狀態，不論什么原因，δ角產生了一個諧波振蕩，用相量Δδ表示，振蕩情況下的轉矩相量如圖1(a)所示。此時設K5＜0，則與K5成正比的電壓偏差中的第一個分量ΔUt1與Δδ反向。勵磁調節器按－ΔUt1調節，它的輸出為ΔEfd，它與－ΔUt1間相角差很小，因為調節器的慣性很小。ΔEfd再輸入勵磁繞組，它的輸出為 ΔMe2，在振蕩過程中，從 － ΔUt1到 ΔMe2的滯后相當于一個0°～90°的相位角。

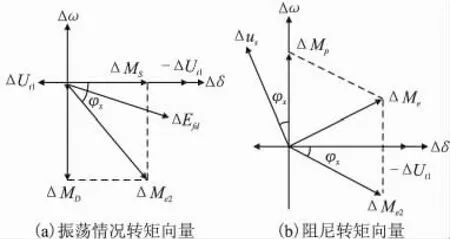
圖1 PSS抑制低頻振蕩轉矩向量圖

2.2 PSS相位補償分析

如圖1(b)所示，電壓調節器產生的附加轉矩ΔMe2落后轉子角振蕩Δδ的相位為φx，如果能產生一個足夠大的純粹的正阻尼轉矩ΔMp，則ΔMp與ΔMe2的合成轉矩就位于第一象限，而它的兩個分量——同步及阻尼轉矩都是正的。上述正阻尼轉矩ΔMp，是在電壓調節器參考點輸入一個附加信號Δus來產生的，因為它的輸入點與ΔUt1的輸入點事實上是同一點，所以要使Δus產生純粹的正阻尼轉矩(相位上與轉速同方向)，Δus的相位必須超前Δω軸φx角，這樣輸入電壓調節器后，經過電壓調節器及勵磁系統的滯后，剛好可以產生純粹的正阻尼轉矩。附加信號Δus即為PSS的輸出，上述過程就是PSS相位補償的原理分析。

3 基于MATLAB的PSS建模

3.1 勵磁調節模塊分析

天生橋二級電站#1機組勵磁調節器是ABB Unitrol－5000型微機勵磁調節器。該勵磁調節器為雙通道勵磁調節器，控制方式采用的是PID+PSS控制。電壓調節器的數學模型如圖2所示，經濾波后機端電壓輸出與PSS的輸出信號UST疊加后作為電壓調節的輸入。電壓調節器包括兩級超前滯后環節和穩態增益KR，最后一級濾波環節是門控單元和整流橋的簡化數學模型。

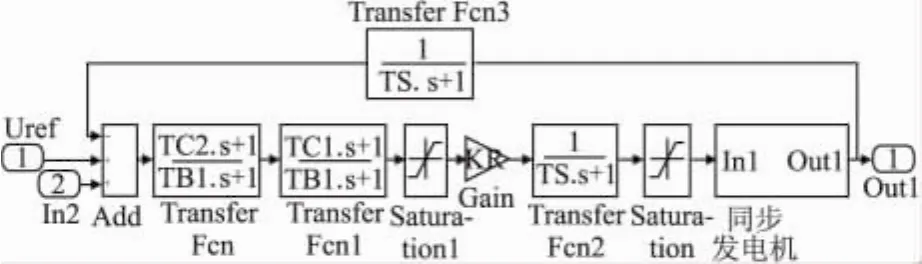
圖2 電壓調節器數學模型

PSS數學模型如圖3所示，包括機械功率計算、陷波器、加速功率計算、相位和增益補償四個環節。PSS的輸入信號為V1和V2。V1表示轉子角頻率的變化量，V2表示機組的電功率。V1和V2首先經過兩級隔直環節后濾出穩態值，得到相應的變化量。電功率信號經兩級隔直和一級濾波后得到其變化量的積分。機械功率的積分來自于V1和V2兩路信號的合成，Ks3用于微調。陷波器用于濾掉有害的高頻分量，比如軸系扭振。加速功率的積分來自于機械功率的積分與電功率積分的差值。最后，兩級超前滯后環節和放大單元Ks1用于相位補償和增益補償。

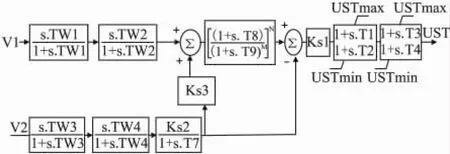
圖3 PSS數學模型

3.2 基于MATLAB的PSS仿真系統

利用Matlab/Simulink功能建立單機無窮大系統如圖4所示，基中AVR與PSS模塊是對上述勵磁調節器和電力系統穩定器的封裝。

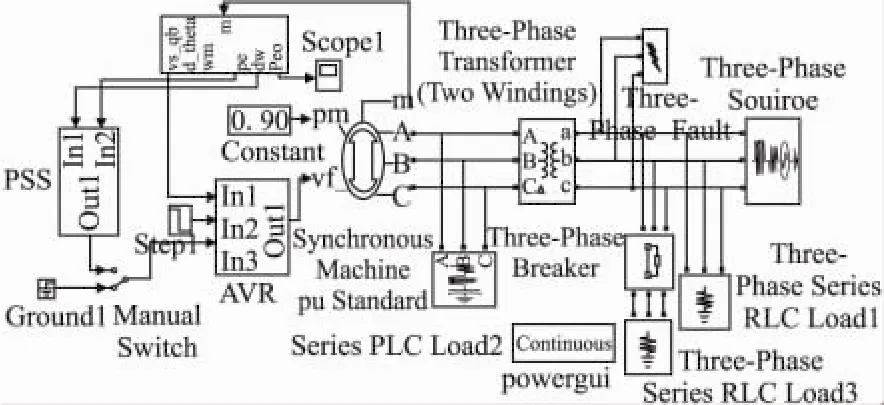
圖4 PSS仿真系統

單機無窮大系統建模需要matlab/simulink如下模塊:

(1)SimPowerSystems工具箱

①Electrical Sources中的Three－Phase Source(三相電源)模塊;

②Elements中的 Three－Phase Series RLC Load(三相串聯RLC負載)模塊，Three－Phase Breaker(三相斷路器)模塊，Three－Phase Fault(三相故障整流器)模塊，Three－Phase Transformer(Two Windings)(三相變壓器繞組)模塊;

③Machines里Synchronous Machine pu Standad(標么標準同步電機)模塊，Machines Measurement Demux(電機復合測量)模塊;

④powergui模塊。

(2)Simulink常用工具箱

①Commonly Used Blocks(常用模塊)中的Constant(常量)模塊，Ground模塊(直流)，Scope(顯示器)模塊;

②Signal Routing(信號路由)模塊庫下的Manual Switch(手動開關)模塊。

4 仿真實驗與結果分析

4.1 仿真實驗參數

同步發電機參數:Pn=245MVA Vn=18kV Xd=1.305p.u.Xd'=0.296p.u.Xd″=0.252p.u.Xq=0.474p.u.Xq″=0.243 p.u.Xl=0.18 p.u.Tdo'=4.7s Tdo″=0.0681s Tq″=0.0513s

勵磁調節器參數:Tr=0.02s TB1=5s TB2=0.08 TC1=1s TC2=0.08s

PSS參數:TW1=2s TW2=2s TW3=2s TW4=0 Ks1=10p.u.Ks2=0.143p.u.Ks1=10p.u.Ks2=0.143p.u.Ks3=1p.u.T1=0.2s T2=0.04 T3=0.44 T4=0.12 T7=2 T8=0.2 T9=0.1

M=5 N=1 USTmax=0.1p.u.USTmin=－0.1p.u.

4.2 相位補償試驗

相位補償實驗利用matlab軟件中Linearization Task功能得到相頻特性曲線。由上文分析，勵磁系統引入PSS后產生的合成電磁轉距在0.1～2.0Hz的范圍內滯后加速轉矩約60°～120°。PSS補償前和PSS補償后系統的相頻特性如圖5所示，除了0.1Hz滯后－57.8，1.4Hz滯后 －134.7，在 0.1 ～2.0Hz的頻率范圍內，有補償相頻特性在－60～－120之間，由PSS產生的電磁力矩的阻尼分量為正，PSS相位補償基本滿足要求。

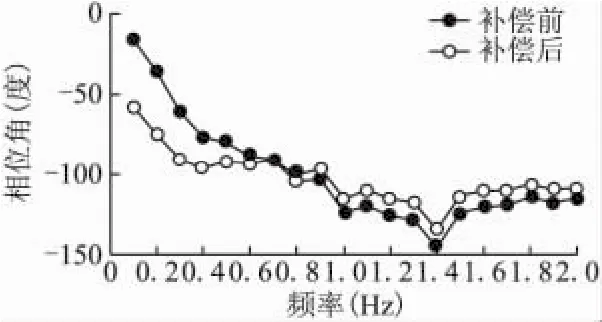
圖5 PSS補償相頻特性

4.3 小擾動實驗

如圖4所示的系統仿真模型分別進行在小擾動下未加和加上PSS的仿真實驗。15s時在機端參考電壓Uref輸入階躍擾動(2%)，25s時線路模擬三相短路故障，0.02s后故障切除。實驗結果如圖6所示，未加入PSS的階躍擾動電功率Pe在20s處停止波動，加入PSS后電功率Pe在17s處停止波動。未加入PSS的三相短路故障電功率Pe在32s處停止波動，加入PSS后在37s處停止波動。通過對比可看出PSS對小擾動有較好的抑制作用。

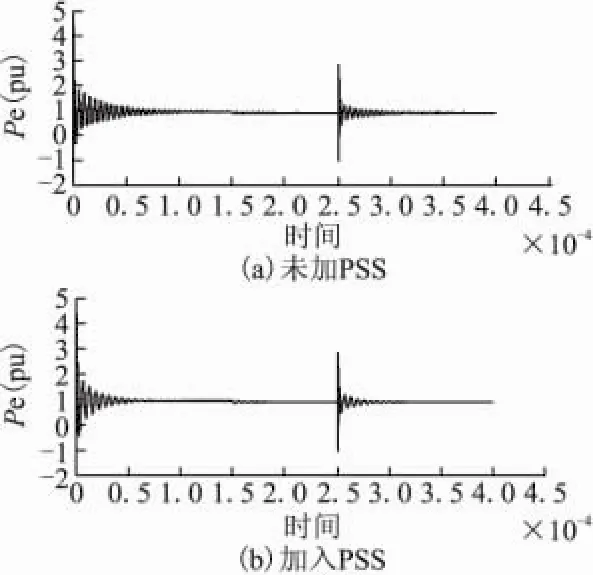
圖6 小擾動實驗Pe時域圖

5 結束語

本文利用轉矩向量分析法分析了低頻振蕩產生的原因，PSS對低頻振蕩抑制的機理。對天生橋二級電站#1機組勵磁調節器模塊數學模型進行介紹，借助Matalb軟件建立了PSS分析模型，并進行實驗分析，結果表明，PSS對系統的低頻振蕩有較好的抑制作用。本文的工作有助于增進對PSS抑制低頻振蕩的理解，為勵磁調節系統分析提供了一個很好的仿真平臺。然而，電力系統是一個復雜的系統，本文在建模分析時并沒有考慮到天生橋二級電站多機組的影響，利用Matlab平臺搭建全廠PSS仿真系統是下一階段工作的重點。

［1］楊梅，李志軍，劉艷萍，等.基于Matlab電力系統穩定器整定［J］.電力自動化設備，2004，24(5):51 －54.

［2］吳峰，陳維榮，李奇，等.基于粒子群優化算法的PSS參數優化［J］.電力系統保護與控制，2009，37(10):53 －58.

［3］韓慧云，黃梅.電力系統低頻振蕩與PSS分析［J］.華北電力技術，2005，7:1 －3.

［4］袁紅斌，張元波，崔國有.淺談電力系統低頻振蕩［J］.東北電力大學學報，2009，29(2):45 －51.

［5］劉取.電力系統穩定性及發電機勵磁控制［M］.北京:中國電力出版社，2007.