內窺式近紅外頻域漫射層析成像圖像重構算法

秦轉萍，趙會娟，楊彥雙

(天津大學精密儀器與光電子工程學院，天津 300072)

漫射層析成像(diffuse optical tomography，DOT)是一種無創功能成像技術[1-4]．目前近紅外漫射光成像的研究大都應用于一些外部器官，如乳房、頭部等[3-4]．采用漫射光進行內窺成像研究開展的較晚，但其研究對于早期宮頸癌和前列腺癌的診斷具有重要的意義．該方法除了具有設備低價、可攜帶以及對操作者水平依賴性低等優點外，更重要的是具有無創性，可通過觀察組織體的新陳代謝狀況而實現在體早期癌癥診斷．國際上進行內窺式漫射光測量及診斷應用研究較早的當屬美國德克薩斯大學的研究組，他們采用近紅外連續光照射、連續光檢測的方法，但結果表明對原位宮頸癌診斷率較低，對癌前組織幾乎沒有辨別能力[5]．2006年由美國 MediSpectra Inc公司生產了漫射光宮頸影像系統[6]，該系統雖然可對宮頸上皮內中、高度瘤變(CIN 2、3)進行診斷，但圖像空間分辨率低，對癌前病變等級分化不清晰，且僅能對外宮頸進行診斷，無法診斷宮頸管內病變．

近紅外漫射光測量系統可分為只提供光強測量量的連續光系統以及可提供多個測量量的時間分辨系統和頻域系統．相對于時間分辨系統，頻域系統具有測量速度快、系統相對簡單等優點．頻域系統采用高頻信號調制光源，通過測量光經過組織體后光子密度波的幅度衰減和相位延遲實現光學參數重構．2006年 Piao等[7]針對前列腺、直腸等組織首次進行了內窺式近紅外頻域漫射光成像，并取得了較好的動物實驗結果．但受檢測設備的限制，其頻域系統只獲得了直流(DC)數據，用 NIRFAST軟件包進行的圖像重構結果表明，目標定位精度受目標病灶深度的影響，定位不準確[7-8]．

筆者研究了針對早期宮頸癌診斷的頻域漫射光層析成像圖像重構方法．首先介紹了所發展的圖像重構理論；其次采用所發展的圖像重構算法，對吸收系數和約化散射系數分別進行重構，以驗證算法的正確性；最后，為與文獻[8]僅利用直流數據進行重構的結果進行比較，在無限和有限2種吸收系數對比度情況下，對吸收系數進行了重構，以驗證本文所提算法可消除目標深度對目標定位精度的影響．

1 圖像重構理論

考慮到實際測量數據的有限性，研究了同時利用頻域測量值中幅值和相位信息的重構方法，用于增加測量數據的信息量，減少逆問題的欠定性和病態性．

1.1 正問題

光子在組織中的傳播模型采用漫射方程的頻域形式，邊界條件采用考慮內反射效應的羅賓邊界條件[9]．以Φ、0ω、c、0q分別表示光子密度、調制頻率、光在組織中的傳播速度、迷向光源，Ω表示成像區域，Ω?表示Ω的邊界，s表示一個源點位置，ξ表示一個探測點位置，D為剖分總節點數．

采用有限元法求解頻域漫射方程，最終得矩陣方程為

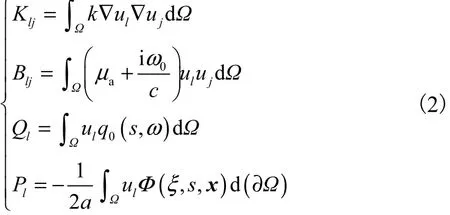
式中：K、B為D×D維矩陣；Φ、Q、P為D×1維矩陣；l、j為節點的整體編號；l, j = 1,2,…,D；μl為第l個節點的形狀函數；Φ (ξ , s ,x)為光源在s處激勵時在邊界ξ處探測到的光子密度；a = ( 1 + Rf) /(1 - Rf)，Rf為擴散傳輸內反射系數；

通過式(1)可求得光子密度Φ，并通過羅賓邊界條件求出探測點處的光子流

頻域測量量的輸出采用Rytov形式，分別用實部和虛部表示幅值和相位，即Γreal=real(ln(Γ (ξ ,s, x ) ))，Γimag=imag(ln(Γ (ξ ,s, x ) ))．

1.2 圖像重構算法

由于組織體的強散射效應、光在組織中的非直線傳播、測量數據的有限性、組織體的非均勻性等因素的影響，近紅外漫射光圖像重構是一個非線性欠定、病態逆問題．采用高斯牛頓法求解該逆問題．正問題算子采用 ()Fx表示．設在宮頸內邊界上采用 S個源點照射、M 個點測量，考慮到在每個測量點可獲得幅度和相位 2個量，總測量數據量為. 則目標函數為

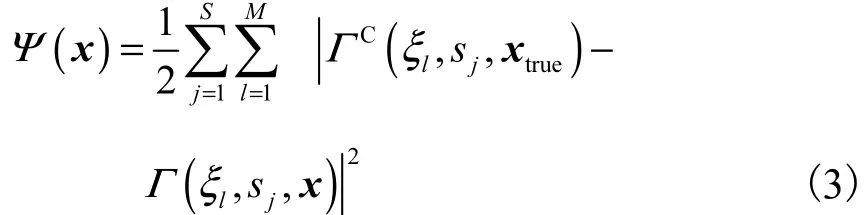
式中 ΓC和Γ分別為測量的和由正問題計算得到的邊界光子流．

對目標函數Ψ ( x)求導，令導數Ψ ′(x ) =0．用泰勒級數對Ψ′(x)在xk附近展開，保留線性項，并采用阻尼最小二乘法(Levenberg-Marquarat，LM)進行正則化．則最終得

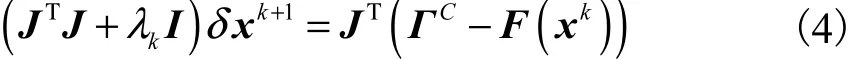
式中：δxk+1為迭代更新因子；I為單位陣；λk為第k次迭代的正則化參數；J為雅可比矩陣，J =[Jμa,Jμs′]；Jμa、Jμs′分別為關于μa和μs′的雅可比矩陣．

當解空間維數非常大時，J的計算非常費時．本研究對J的求解采用伴隨源法，此方法僅用2次正向求解便可實現對 J的構建，可簡化計算，大大減少計算時間．但是 Jμs′的構建涉及到對光子密度求梯度，這不僅耗時，而且在源點附近顯示出某些數值上的奇異性，從而導致算法對于組織體深層散射信息不敏感．基于此情況，采用了修正廣義脈沖譜技術，此技術利用了強散射媒質 μs′ ＞＞μa的性質、散度定理及頻域漫射方程，對進行了近似求解[2,10-11]307-329．同時 J采用 Rytov近似，則最終可獲得Jμa、Jμs′的表達式為

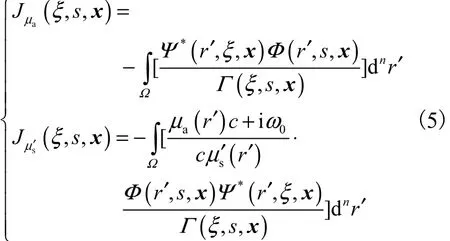
式中：r′為區域Ω內任意一點的位置；Ψ*(r ′ ,ξ,x)為源放在探測點ξ處進行激勵、由伴隨理論求得的r′處的光子密度的共軛值．

在頻域內J的結構為

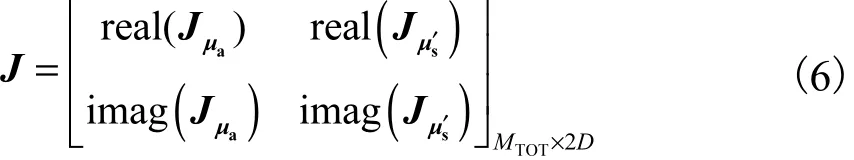
當 J的維數非常大時，不僅求解方程(4)非常費時，而且存儲Hessian矩陣(JΤJ)會占用非常大的內存，這一問題對于三維成像尤為重要．為了解決此問題，采用廣義最小余量(generalized minimal residual，GMRES)Krylov方法進行求解[1]．

如第k次迭代后滿足中止條件，則用 xk來近似真實值 xtrue．

2 光學參數重構精度的驗證

2.1 用于圖像重構的組織模型

考慮到子宮頸的尺寸和形狀，成像區域為圓環模形，其中圓環內半徑為 10,mm，外半徑為 20,mm，源點和探測點在內環邊界上．由于內環尺寸較小，在漫射方程適用范圍內[12]107-111，最終選用16個源點和16個探測點，如圖 1所示．每次僅在一個源點激勵，所有探測點同時獲得測量數據，然后換作另一個源點激勵并測量，直到所有源點完成激勵．

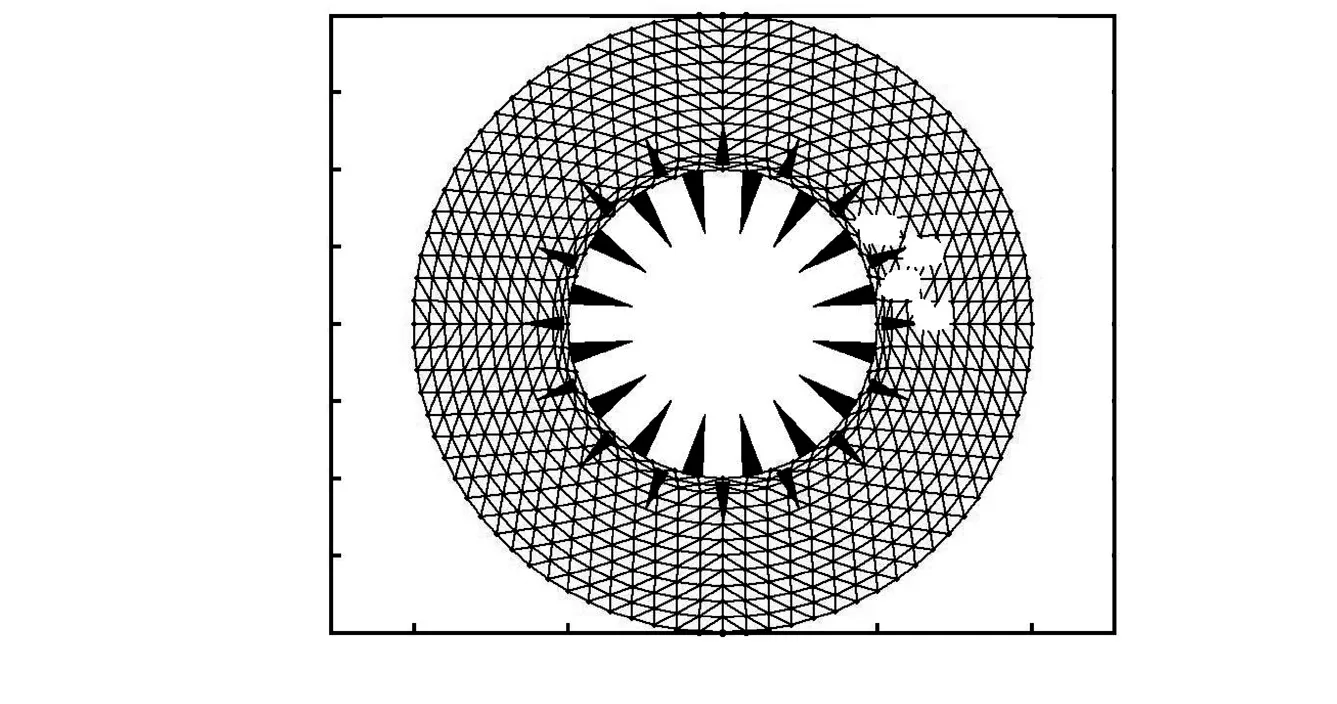
圖1 成像區域及源和探測點分布Fig.1 Imaging domain and the distribution of 16 sources and 16 detectors

2.2 吸收系數和約化散射系數的重構精度

為了評價重構出的圖像的質量，分別采用保真度和半寬度來評價重構出的光學參數值和重構出的目標尺寸大小，其中保真度定義為 ( max μconstruct?μB)/(μobject?μB)μB，為背景組織的吸收或約化散射系數．

設圖1中背景組織體的光學參數為μaB=0.01mm?1、= 1 mm?1，假設在上述成像域內有2個病灶，半徑均為 2,mm．病灶的光學參數分別為：μa1=3μaB，μs′1= μs′B，μa2=μaB，μs′2= 2 μs′B．病灶中心坐標分別為(－14，0)和(14，0)，如圖 2(a)和(b)所示．

圖2 aμ和′sμ的目標圖像和重構圖像(aμ對比度3∶1，sμ′對比度2∶1)Fig.2 Image ofaμand′sμwith target and recon-structed images from simulated data(contrast levels foraμ and sμ′ are 3∶1 and 2∶1，respectively)

將圖 2(c)和(d)的重構圖像和目標圖像進行對比可見，重構目標病灶方位和尺寸基本同目標圖像一致．并且重構目標病灶的位置基本都在真實邊界內(實線圓)，證明了重構位置的準確性．分別取圖 2(a)和(b)沿過病灶中心的水平方向和垂直方向上的目標值和重構值進行比較，結果如圖3所示．可見aμ和sμ′重構的保真度可達81.0%和81.2%．并且aμ圖像中，水平方向和垂直方向的重構目標值半高寬分別為3.50,mm和4.67,mm，sμ′2個方向的半高寬分別為3.56,mm和4.83,mm，與真實病灶直徑(4,mm)對比可見，重構的目標病灶尺寸基本準確．

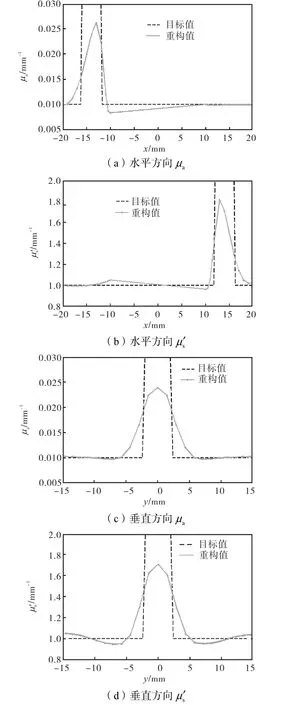
圖3 圖2中水平和垂直方向上目標值和重構值比較Fig.3 Comparison of reconstruction accuracies along the horizontal dashed line and the vertical dashed line in Fig.2

為進一步驗證算法的正確性，令病灶與背景組織體的光學參數的對比度發生變化，μa1= 2 μaB，μs′1= μs′B，μa2=μaB，μs′2= 3 μs′B，其他條件與圖 2圖像重構條件類似，目標圖像如圖 4(a)和(b)所示．重構圖像見4(c)和(d)．

將重構圖像和目標圖像進行對比可見，重構位置準確．同樣，分別取圖 4(a) 和(b)沿過病灶中心的水平方向和垂直方向上的目標值和重構值進行比較，結果如圖5所示．μa和μs′重構的保真度分別可達82%和66.7%．另外μa圖像中水平方向和垂直方向重構目標值的半高寬分別為3.50,mm和4.83,mm，μs′ 2個方向的半高寬分別為 3.81,mm 和 4.67,mm．可見μa和μs′的重構目標值的半高寬基本同真值的直徑(4,mm)相同，證明重構目標病灶尺寸基本準確．

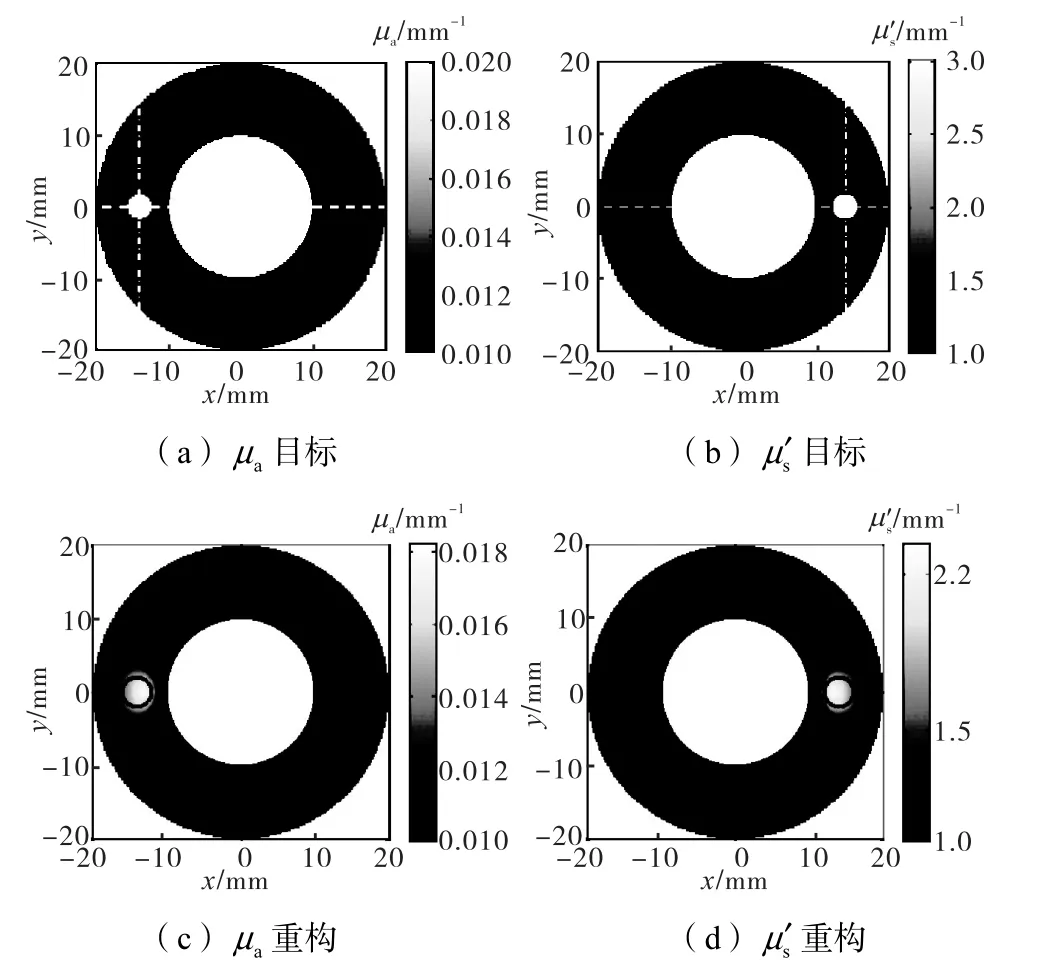
圖4 aμ和′sμ的目標圖像和重構圖像(aμ對比度2∶1，sμ′對比度3∶1)Fig.4 Image ofaμand′sμwith the target and the reconstructed images from the simulated data(the contrast levels foraμandsμ′are 2∶1 and 3∶1，respectively)

另外，在對比度與圖 2類似的條件下，還分別對背景組織體光學參數的變化、病灶方位的變化、病灶半徑的變化對重構精度的影響進行了驗證，結果如表1～表3所示．表中R為病灶的半徑，(x，y)為病灶的中心坐標，Lx、Ly分別為與x、y軸平行且過病灶中心直線上重構圖像的半高寬．表1為R＝2,mm，μa的(x，y)＝(－14，0)，μs′的(x，y)＝(14，0)時，背景組織體光學參數的變化對重構精度的影響；表2為R＝2,mm，μ =0.01mm?1，μ′= 1 mm?1時，病灶方位的aBsB變化對重構精度的影響；表 3為 μ =0.01mm?1，

aBμ′=1mm?1，μ的(x，y)＝(－14，0)，μ′的(x，y)＝sBas(14，0)時，病灶半徑R的變化對重構精度的影響．

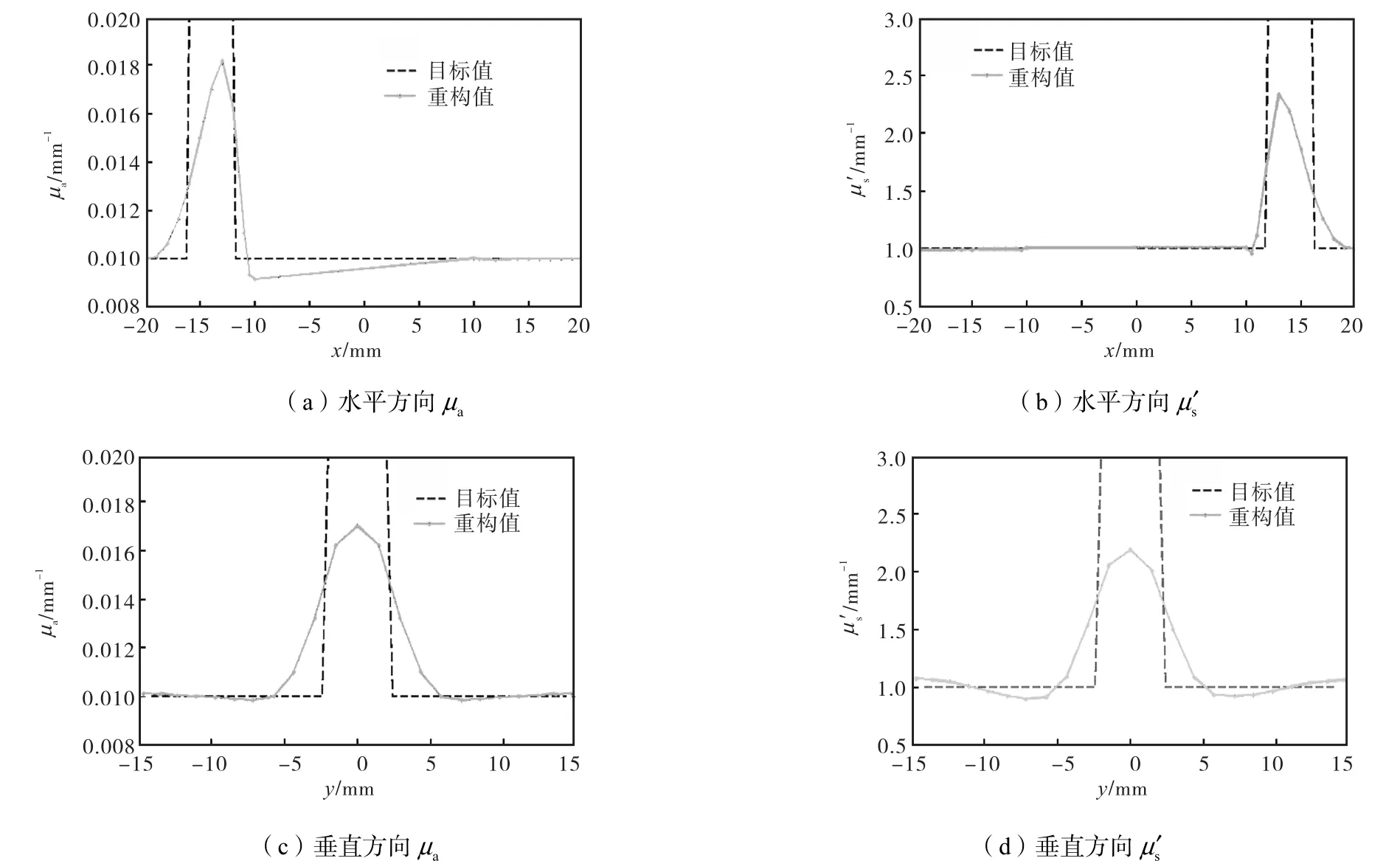
圖5 圖4中水平和垂直方向上目標值和重構值比較Fig.5 Comparison of reconstruction accuracies along the horizontal dashed line and the vertical dashed line in Fig.4

表1 背景組織體光學參數不同對aμ和′sμ重構精度影響Tab.1 Independent reconstruction ofaμand′sμfrom simulated data with different background optical properties

表2 病灶方位不同對aμ和′sμ重構精度影響Tab.2 Independent reconstruction ofaμand′sμfrom simulated data with different positions of target

表3 病灶半徑不同對aμ和′sμ重構精度影響Tab.3 Independent reconstruction ofaμand′sμfrom simulated data with different sizes of target

由表 1～表 3可見，背景組織體光學參數、病灶方位分別發生變化時，重構的aμ和sμ′保真度的變化都在3%以內，并且水平方向和垂直方向上重構值的半高寬幾乎不受上述因素的影響；但病灶半徑發生變化時，病灶半徑越大，重構精度越高，而病灶半徑變小時，重構保真度下降嚴重且重構目標病灶的尺寸展寬嚴重．

3 目標深度對目標定位精度的影響

為了和文獻[8]進行對比，在以下圖像重構中，僅利用頻域的DC數據對吸收系數進行圖像重構，且設仿組織體的內半徑為 10,mm，外半徑為 30,mm，源點和探測點均為8個，和圖1排列方式相同，背景組織體的光學參數為 μ =0.002mm?1，μ′= 0 .5mm?1，病aBsB灶的直徑為7.70,mm．在2種吸收系數對比度下進行圖像重構，其中 μa=100μaB，μs′= μs′B代表無限吸收對比度，μ =0.0059mm?1，μ′= 1 .03mm?1代表有限吸收as對比度．

文獻[8]中無限吸收對比度的仿真結果顯示：當病灶中心在(0，15)時，重構目標病灶的位置基本正確；當中心在(0，20)、(0，25)時，重構目標病灶的位置幾乎仍在(0，15)不變，重構出的病灶尺寸變大．在上述條件下，采用本文的算法進行圖像重構，結果顯示：中心坐標在(0，15)、(0，20)、(0，25)這 3 個位置處，重構目標病灶的方位與真值相同．此結果表明在無限吸收對比度的情況下，本文的算法所重構的結果在目標方位上不受目標深度的影響．

文獻[8]中有限吸收對比度的仿真條件為：背景組織體的光學參數不變，病灶中心的坐標分別為(0，15)、(0，17)、(0，19)，如圖 6(a)～(c)所示．文獻[8]的仿真結果顯示：病灶中心在(0，15)時，重構目標病灶的位置基本正確．當中心在(0，17)時，重構目標病灶的位置仍在(0，15)．當中心在(0，19)時，重構目標病灶的中心在(10.6，－10.6)，重構的目標病灶方位產生了很大的偏差．

在上述條件下，采用本文的算法所重構的圖像如圖 6(d)～(f)所示．可見病灶中心在(0，15)、(0，17)、(0，19)時，重構目標病灶的位置基本與真值位置(實線圓)重合．此結果證明了在有限吸收對比度的情況下，本文算法所重構的結果在目標方位上也不受目標深度的影響．3個位置處aμ重構的保真度分別為 97.4%、69.2%、51.3%，可見隨著病灶離內邊界距離的增大，aμ重構保真度變差．當病灶中心位于(0，15)時，重構目標病灶的水平和垂直方向的半高寬分別為 7.70,mm 和 5.50,mm；(0，17)時，半高寬分別為10.16,mm 和 8.80,mm；(0，19)時，半高寬分別為13.86,mm和 9.90,mm．與真實直徑(7.70,mm)對比可見，隨著病灶離內邊界距離的增大，重構的病灶尺寸也隨之增大．

為了改善保真度和重構目標尺寸的準確性，本文還同時利用頻域測量值的幅值和相位信息進行圖像重構，結果如圖7所示．

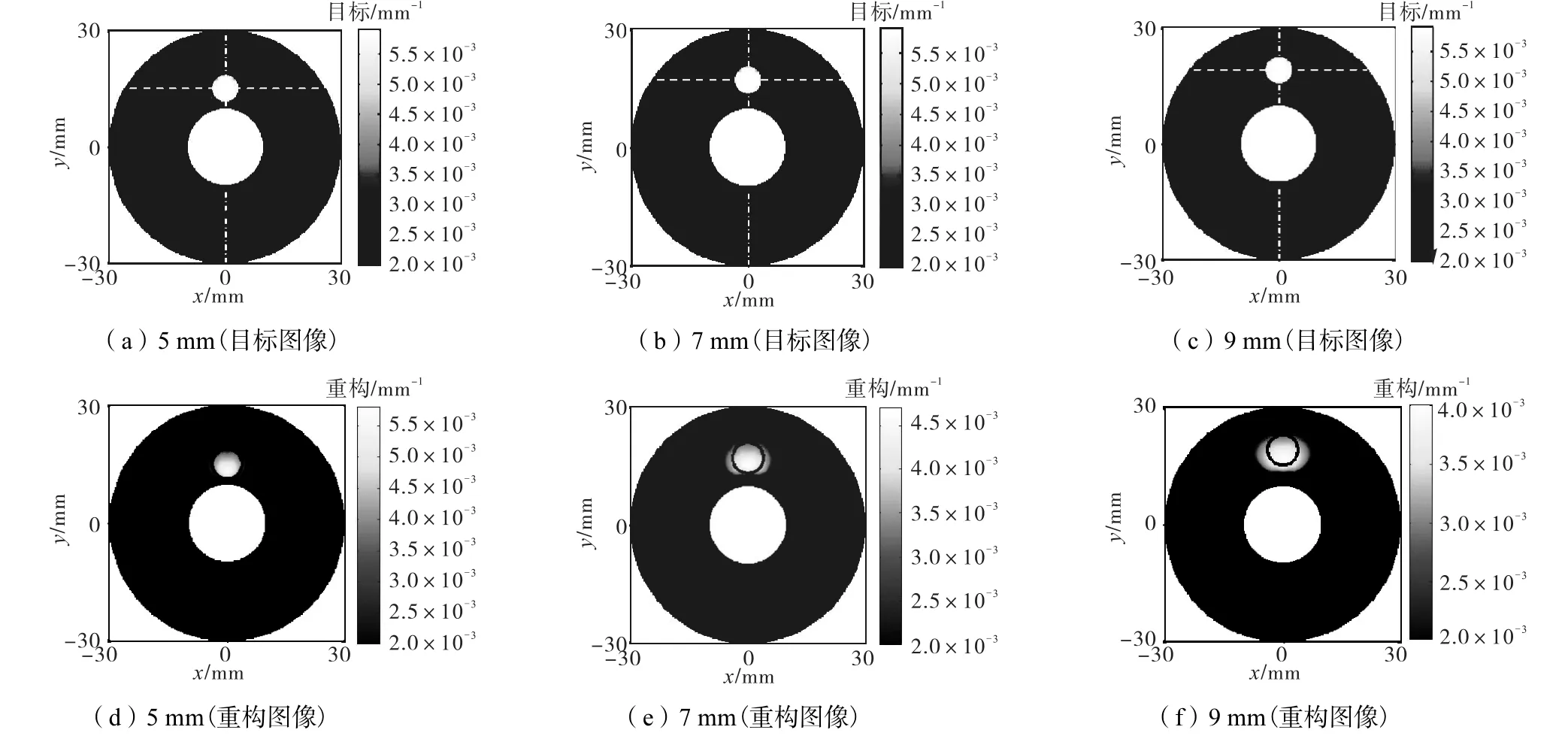
圖6 病灶處于不同深度時僅利用DC數據的圖像重構結果Fig.6 Reconstructed images for targets at different depths using only DC data

可見重構目標病灶的位置完全在真實邊界內(實線圓)．3個位置處aμ重構的保真度分別為112.8%、89.7%、66.7%；當病灶中心位于(0，15)時，重構目標病灶的水平和垂直方向的半高寬分別為 7.70,mm和7.43,mm；(0，17)時，半高寬分別為 9.15,mm 和8.21,mm；(0，19)時，半高寬分別為 11.17,mm 和9.75,mm．將圖 6和圖 7的重構結果進行對比可見，同時利用頻域的幅值和相位信息，不僅保真度有所提高，而且重構目標病灶的尺寸更接近于真實病灶．

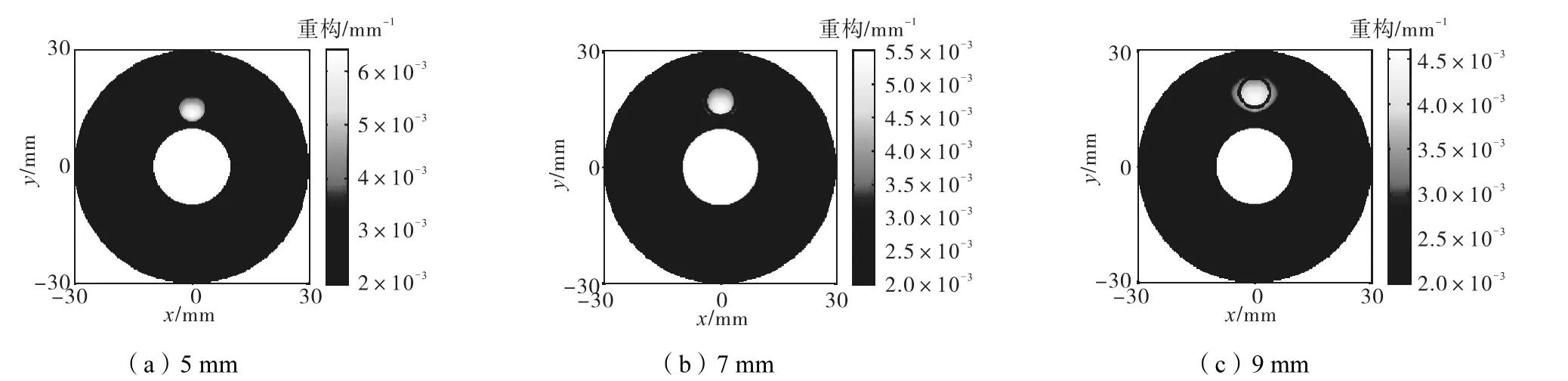
圖7 病灶處于不同深度時同時利用頻域幅值和相位信息的圖像重構結果Fig.7 Reconstructed images for targets at different depths using both amplitude and phase parts of frequency domain

4 結 語

針對于用于早期宮頸癌診斷的內窺式近紅外頻域漫射層析成像，本文研究了同時利用頻域測量值中幅值和相位信息的重構方法．正問題采用有限元法求解，逆問題采用高斯牛頓理論．雅可比矩陣采用伴隨源法進行構建，并采用修正的廣義脈沖譜技術．迭代更新因子采用GMRES Krylov方法求解．

圖像的重構結果表明：對aμ和sμ′進行單獨重構時，重構目標的位置、大小準確度較高．雖然重構值的精度受對比度、背景組織體的光學參數、病灶方位、病灶大小等因素的影響，但重構aμ和sμ′保真度可達 80%，證明了本文算法的正確性；為了與文獻[8]進行比較，在無限吸收對比度和有限吸收對比度這 2種情況下僅利用 DC數據進行了圖像重構，結果表明：本文所發展的算法可消除目標定位精度受目標深度影響的問題．并且同時利用頻域測量值的幅值和相位信息可提高重構的精度．

［1］ Schweiger M，Arridge S R，Nissila I. Gauss-Newton method for image reconstruction in diffuse optical tomography[J]. Physics in Medicine and Biology，2005，50(10)：2365-2386.

［2］ Arridge S R. Optical tomography in medical imaging [J].Inverse Problems，1999，15：R41-R93.

［3］ Brooksby B，Jiang S，Dehghani H，et al. Combining near-infrared tomography and magnetic resonance imaging to study in vivo breast tissue：Implementation of a Laplacian-type regularization to incorporate magnetic resonance structure [J]. Journal of Biomedical Optics，2005，10(5)：1-10.

［4］ Xu H，Dehghani H，Pogue B W，et al. Near-infrared imaging in the small animal brain：Optimization of fiber positions[J]. Journal of Biomedical Optics，2003，8(1)：102-110.

［5］ Mirabal Y N，Chang S K，Atkinson E N，et al. Reflectance spectroscopy for in vivo detection of cervical precancer[J]. Journal of Biomedical Optics，2002，7(4)：587-594.

［6］ Kendrick J E，Huh W K，Alvarez R D，LUMATMcervical imaging system[J]. Expert Review of Medical Devices，2007，4(2)：121-129

［7］ Piao Daqing，Xie Hao，Musgrove C，et al. Nearinfrared optical tomography：Endoscopic imaging approach [J]. Proceedings of SPIE，2007，6431：1-10.

［8］ Musgrove C，Bunting C F，Dehghani H，et al. Computational aspects of endoscopic(Trans-rectal)nearinfrared optical tomography：Initial investigations[J].Proceedings of SPIE，2007，6434：1-10.

［9］ Schweiger M，Arridge S R，Hiraoka M，et al. The finite element method for the propagation of light in scattering media：Boundary and source conditions[J].Medical Physics，1995，22(11)：1779-1792.

［10］ Gao Feng，Zhao Huijuan，Tanikawa Y，et al. Timeresolved diffuse optical tomography using a modified generalized pulse spectrum technique [J]. Ieice Transactions on Information and Systems，2002，E85-D(1)：133-142.

［11］ Sebbah P. Waves and Imaging Through Complex Media[M]. Holland：Klumer，2001.

［12］ Wang Lihong V，Wu Hsin-i. Biomedical Optics[M].New York：John Wiley and Sons Inc，2007.