基于奇異譜分析的匯率預測研究
張 一,惠曉峰
(哈爾濱工業大學 經濟與管理學院,哈爾濱 150001)
0 引言
對匯率預測的研究多年來一直是國際金融界的一個重要課題。自Messe和Rogoff[1]于1983年建立了簡單的隨機游走模型并證實其預測效果優于其它模型后,關于匯率預測的研究方法不斷涌現。堅持有效市場假說的學者們認為匯率是由獨立的、隨機的變量產生的白噪聲信號,即匯率不可預測。堅持匯率決定理論的學者們則主要從基于基礎變量預測法和技術預測法兩個方向進行研究。基礎變量法主要考慮的變量是價格水平、利率基準、貨幣供應量、國民收入、外匯儲備等因素并形成了不同的理論,如購買力平價理論[2~4]、利率平價理論[5]、國際收支理論等。由于經濟基礎變量在短時期內變化很小,所以在解釋匯率短期波動上并沒有取得很好的效果。技術預測法則從時間序列數據本身出發,通過歷史數據來進行預測,如ARMA模型,ARIMA模型,ARCH模型,GARCH模型等。這些模型主要是用過去變化和過去方差來預測將來的變化,可有效地排除資產收益率中的過度峰值,并取得了較好的預測效果。
近年來,非線性動力學的快速發展為資產價格的預測提供了新的研究方法。這種方法主要是通過時間延遲和相空間重構技術,將所觀測到的時間序列數據還原成代表其動力學特征的高維相空間,并將其看做是由其動力系統的吸引子產生的相空間軌跡的一部分[6~8]。由于金融市場具有非線性、不連續等內在特征,使得該方法在這一領域取得了很好的應用效果。
奇異譜分析(SSA)是近年來興起的一種研究非線性時間序列數據的強大的方法。它根據所觀測到的時間序列構造出軌跡矩陣,并對軌跡矩陣進行分解、重構,從而提取出代表原時間序列不同成分的信號,如長期趨勢信號、周期信號、噪聲信號等,從而對時間序列的結構進行分析,并可進一步預測。奇異譜分析目前較多地應用在氣象學和地質學的研究中,并有少量學者將其引入到社會問題研究中。由于這種方法不需要對模型進行假設,是一種非參數估計法并且不需要各種經濟指標數據,不存在模型設計和過度擬合等問題,所以同樣適合于金融時間序列的分析。
1 方法介紹
1.1 奇異譜分析方法
奇異譜分析(SSA)方法最早由colebrook[9]于1978年首先在海洋學研究中提出并使用。Fracrich[10]用一維時間序列在延遲相空間中做EOF展開,再通過顯著性檢驗研究確定有意義的特征成分的個數,據此估計氣候吸引子的維數。這個工作被認為是SSA在氣象學中的最早應用。Hassani[11]將這種方法引入到社會問題研究中來,并用其預測了美國交通事故的月時間序列數據。N.Golyandina[12]給出了奇異譜分析的擴展形式-多通道奇異譜分析的算法,并由Hossein Hassani[13]用來對英鎊/美元匯率進行了分析預測,取得了較好的效果。目前,國內應用這一方法研究金融領域問題的文獻并不多,主要有徐海云[14]對我國貨幣供應量進行了分析,呂紅[15]用其對上證指數預測等。更多關于奇異譜分析方法的介紹可參考文獻[16~20]。
奇異譜分析的基本思想是,將所觀測到的一維時間序列數據YT=(y1,…,yT)轉化為其軌跡矩陣:
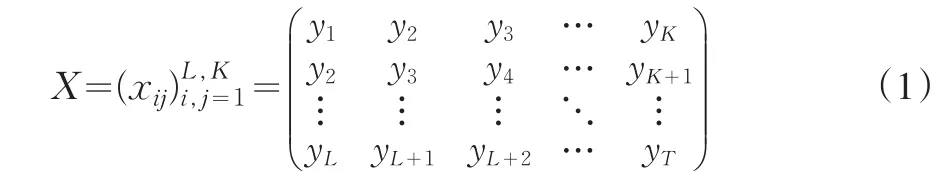
其中,L為選取的窗口長度,K=T-L+1,計算XXT并對其進行奇異值分解(SVD),從而得到其L個特征值λ1≥λ2≥…≥λL≥0及其相應的特征向量將每一個特征值所代表的信號進行分析組合,重構出新的時間序列。奇異譜分析過程可分成嵌入、SVD分解、分組、重構四個步驟,下面詳細介紹具體算法。
1.2 算法
1.2.1 嵌入
選擇適當的窗口長度L(2≤L≤T),將所觀測到的一維金融時間序列數據轉化為多維序列X1,…,XK,,得到軌跡矩陣。這里L的選取不宜超過整個數據長度的1/3,如可根據事先經驗大致確定數據的周期特征,則L的選取最好為周期的整數倍。
1.2.2 SVD分解
計算XXT并求得其L個特征值λ1≥λ2≥…≥λL≥0,U1,…,UL為其所對應的正交特征向量,另d=max(i,λi>0)=R(A),則

1.2.3 分組
將(2)式中的Xi分成幾個不同的組并將每組內所包含的矩陣相加,另{i1,…ip}為第I組所包含的矩陣,則XI的貢獻率為

1.2.4 重構
將矩陣XI轉換成其所對應的時間序列數據,每一組數據代表原序列的某一運動特征,如長期趨勢,季節性趨勢,噪聲信號等。設zij為矩陣Z所對應的元素,則第k個時間序列數據為滿足i+j=k+2的所有z的平均值,ΗZ為新獲得的時間序列的軌跡矩陣。以此來求式(4)中的每一個矩陣,則可得
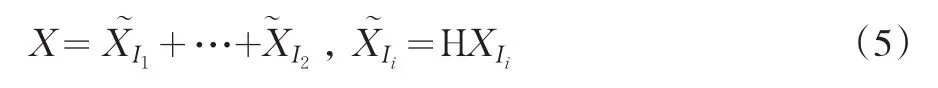
原序列YT=(y1,…,yT)可表示成

1.3 預測
線性遞歸過程是將序列某一點的數據用其前d個數據的線性組合來計算
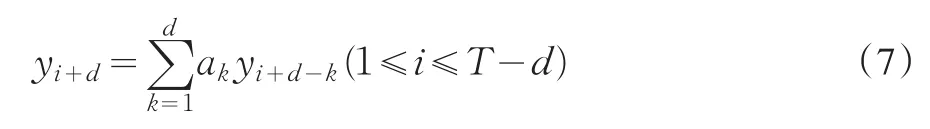
用線性遞歸模型對(5)式中的重構序列進行預測,得到預測數據,并進一步將預測結果與隨機游走模型進行比較
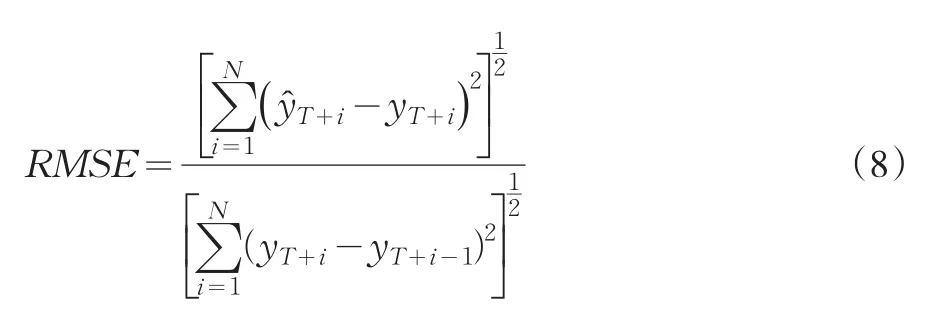
RMSE為均方根誤差,N為預測數據個數。
若RMSE≈0或是很小,說明預測結果相當精確;
若RMSE<1,說明該方法預測結果優于隨機游走模型;
若RMSE>1,說明該方法預測結果比隨機游走模型差。
同時計算檢驗統計量
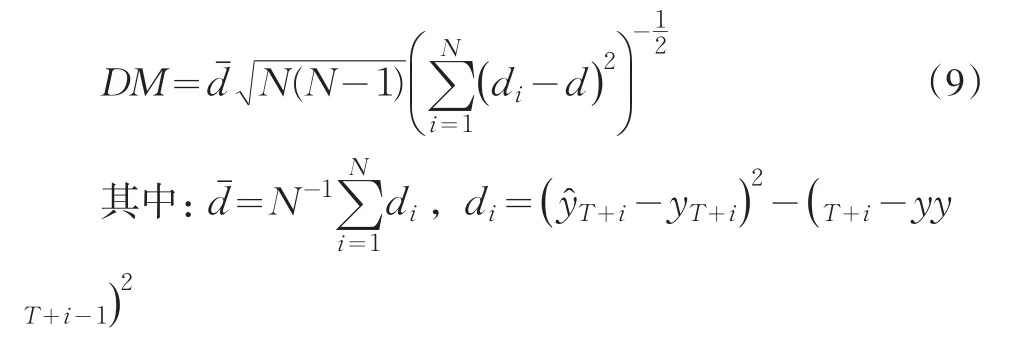
當DM結果為負,且絕對值越大,表明預測結果越是顯著地優于隨機游走模型。
2 實證結果
2.1 數據分析結果
2.1.1 數據選取與預處理
本文選取歐元兌美元匯率作為研究對象,樣本區間為2000年1月1日至2007年12月1日,共1505個觀察值。在進行具體分析前,先將數據標準化:yt→yt/||Yt||t=1,…,T,其中結果如圖1所示。
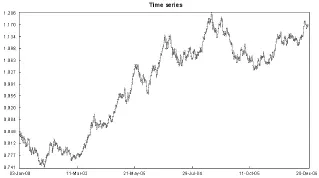
圖1 歐元/美元時間序列數據
2.1.2 趨勢分析
選取窗口長度L=30對序列進行分析重構,并提取第一個特征值為代表數據長期趨勢的主要成分,結果如圖2所示。
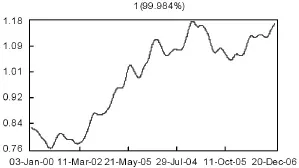
圖2 序列的長期趨勢成分
對特征值1所代表的成分進行對角線平均,得到重構后的時間序列數據。特征值2~30為噪聲信號,分析結果如圖3、圖4所示。

圖3 主成分信號

圖4 噪聲信號
2.2 預測結果比較
用圖3所示的新獲得的數據進行預測,預測方法為(7)式所示的線性遞歸過程,向后預測40個數據,并與真實數據比較,進一步根據(8)式求得根均方誤差,并計算(9)式中的檢驗統計量,如表1所示。
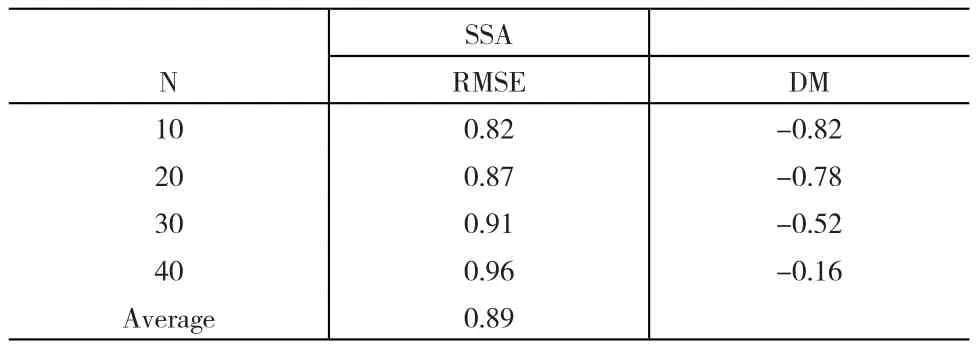
表1 預測結果
由表1預測結果可見,在預測短期匯率時,SSA分析方法優于隨機游走模型,但隨著預測數據的增多,結果逐漸變得不顯著。
3 結論
本文對奇異譜分析方法進行了詳細的介紹并用其對匯率預測問題進行了實證檢驗。結果表明,在進行短期匯率預測時,用該方法得到的預測結果優于隨機游走模型,預測精度比較理想。奇異譜分析是一種比較新的且功能強大的處理時間序列的分析方法,可用于提取時間序列的主要成分、降噪、預測等很多方面。所以可將其進一步應用于其他的經濟及金融時間序列分析問題中。同時,其擴展形式多通道奇異譜分析(MSSA)、復雜奇異譜分析(CSSA)也是可以進一步深入研究的方向。
[1] R.Meese,K.Rogoff.Empirical Exchange Rate Models of the Seven?ties:Do They Fit Out-of-sample[J].Journal of International Econom?ics,1983,(14).
[2] J.Frankel,K.A.Froot.Chartists,Fundamentalists,and Trading in the Foreign Exchange Market[J].American Economic Review,1990,(80).
[3] J A Frenkel.Flexible Exchange Rates,Prices,and the Role of‘News’:Lessons from the 1970’s[J].Journal of Political Economy,1981,(89).
[4] D Corbae,S Ouliaris.Cointegration and Tests of Purchasing Power Parity[J].Eview of Economics and Statistics,1988,(70).
[5] M.D.Chinn,G.Meredith.Monetary Policy and Long Horizon Uncov?ered Interest Parity[R].IMF Staff Papers,2004,(51).
[6] A.Soofi,L.Cao.Modelling and Forecasting Financial Data:Tech?niques of Nonlinear Dynamics[R].Boston:Kluwer Academic Publish?ers,2002.
[7] A.Soofi,A.Galka.Measuring the Complexity of Currency Markets by Fractal Dimension Analysis[J].International Journal of Theoretical and Applied Finance,2003,(6).
[8] L.Cao,A.Soofi.Nonlinear Deterministic Prediction of Daily Dollar Exchange Rates[J].International Journal of Forecasting,1995,(15).
[9] Vautard.SSA:A Toolkit for Noisy Chaotic Signals[J].Physics D,1992,(58).
[10] Fracrich.Estimitating the Dimensions of Weather and Climate At?tractors[J].JAS,1986,(43).
[11] Hassani Hossein.Singular Spectrum Analysis:Methodology and Com?parison[J].Journal of Data Science,2007,(5).
[12] N.Golyandina,D.Stepanov.SSA-based Approaches to Analysis and Forecast of Multidimensional Time Series[C].Proceedings of the Fifth Workshop on Simulation,2005.
[13] H.Hassani,A.Soofi.Predicting Daily Exchange Rate with Singular Spectrum Analysis[J].Nonlinear Analysis:Real World Applications,2010,(11).
[14] 徐海云,陳黎明.我國貨幣供應時序結構的奇異譜分析[J].財經理論與實踐,2010,(31).
[15] 呂紅,費文龍.基于奇異譜分析的上證指數預測模型[J].南京理工大學學報,2003,(27).
[16] N.Golyandina,V.Nekrutkin,A.Zhigljavsky.Analysis of Time Se?ries Structure:SSA and Related Techniques[M].New York:Chapman&Hall/CRC,2001.
[17] D.Danilov,A.Zhigljavsky.Principal Components of Time Series:The‘Caterpillar’Method[R].University of St.Petersburg Press,1997.
[18] J.B.Elsner,A.A.Tsonis.Singular Spectral Analysis,A New Tool in Time Series Analysis[M].New York:London Plenum Press,1996.
[19] H.Hassani,S.Heravi,A.Zhigljavsky.Forecasting European Indus?trial Production with Singular Spectrum Analysis[J].International Journal of Forecasting,2008,(10).
[20] V.G.Moskvina,A.Zhigljavsky.An Algorithm Based on Singular Spectrum Analysis for Change-point Detection[J].Communication in Statistics-Simulation and Computation,2003,(32).

