自相關過程的ARMA控制圖

張志雷

（河南財經政法大學統計學系，鄭州 450002）

0 引言

為了解決過程自相關條件下的質量控制問題，人們提出了多種方法。由于自相關過程的統計控制狀態可由時間序列的模型和參數來描述，因此，時間序列理論作為一種重要的方法被普遍用于解決自相關過程的控制問題。其中常見的一種思想是運用時序模型擬合的方法把自相關過程過濾成殘差序列，由于殘差序列獨立同分布，因此可采用常規控制圖進行控制，形成的控制圖稱為殘差控制圖[1]（以下簡稱殘差圖），研究表明：殘差圖適用范圍有一定局限性，當過程中、強度正相關且均值發生較大偏移時，殘差圖具有較好的使用價值[2]。另有學者則提出根據過程自相關結構，運用時序理論重新構造控制圖的過程控制統計量，以達到提高控制圖檢測性能的目的。本文依據控制圖設計基本思想，研究建立在自回歸移動平均統計量基礎上的ARMA控制圖原理，并以鏈點檢出概率和平均鏈長(ARL)為準則，系統分析了ARMA控制圖的性能，并與殘差圖進行了較為系統的比較，結果有助于我們清楚認識生產中自相關過程的控制問題從而正確選用適宜的控制圖。

1 ARMA控制圖基本原理[3]

假設X1,X2,…是離散平穩序列，具有不變的均值和自相關結構，即E(Xt)=m(t∈Z),自協方差函數g(t)=cov(Xt,Xt+t)僅與滯后期t有關。根據時間序列理論中的ARMA模型，構造出ARMA控制圖的統計量Zt可表示為：

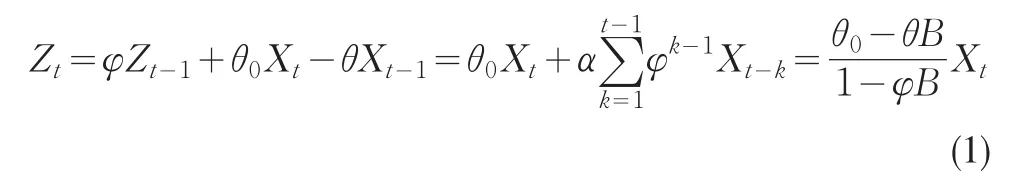
其中α=φθ0-θ，B為滯后算子。根據Zhang協方差計算方法【4】可證明式(1)中統計量Zt在自相關條件下也為平穩序列。易證E(Zt)=m,而序列{Zt}的自協方差函數是：

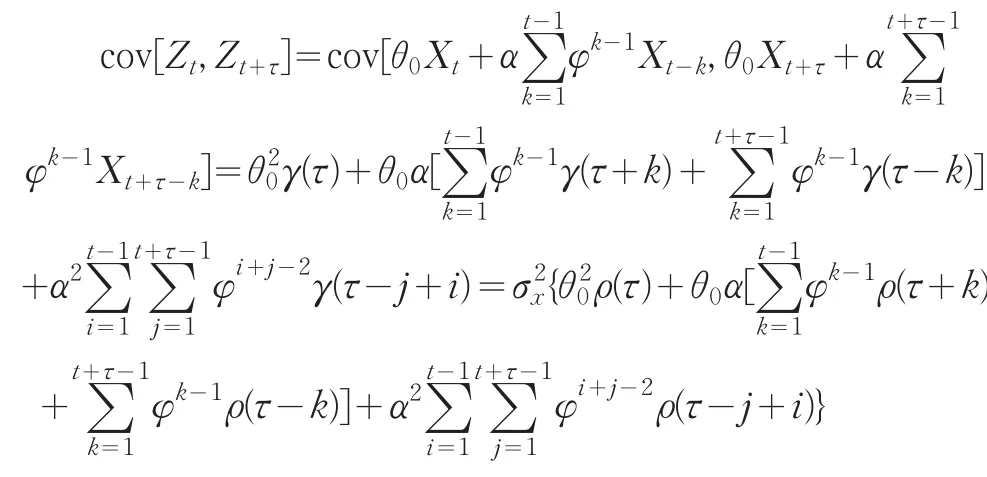
其中r(t)=g(t)/g(0)是序列{Xt}滯后t期的自相關系數。若t→∞且t＝0時，上式則為控制統計量Zt的方差：

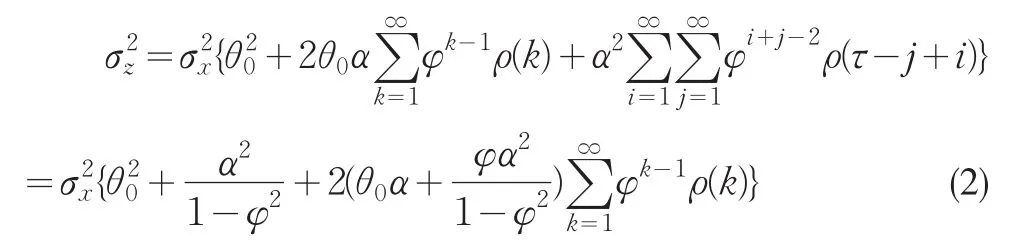
被檢測過程的自相關形式可以用不同的時序模型來刻畫，為具體說明ARMA控制圖的基本原理,本文采用具有代表性的ARMA(1,1)模型表示被測過程，其形式為：

其中 ∣u∣＜1,∣v∣＜1，at～N(0,)。其方差和滯后一期的相關系數分別為：

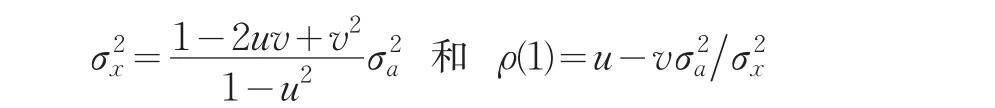
那么，可用ARMA(1,1)模型關系式來簡化穩定狀態下Zt的方差，將以上兩個公式帶入到式(2)中并由r(k)=ur(k-1)（其中k≥2）可得：

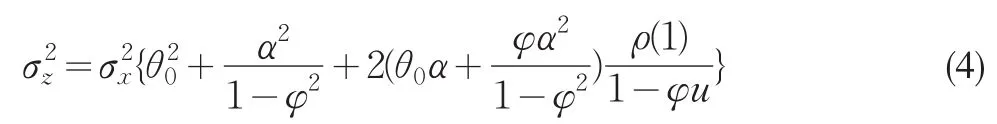
因為Xt服從正態分布，所以Zt也服從正態分布，均值為μ，當t很大時，使用式(4)計算被測過程ARMA(1,1)的σz值。由統計量Zt，可建立ARMA控制圖，其中心線為μ，上下控制限為μ±kσz。在用ARMA控制圖進行控制時，由于受控過程Xt和檢測過程Zt都為自相關過程，觀測點在控制界限內呈現非隨機排列的可能性大大增加，如連續七點單調上升或單調下降，因此僅用觀測點是否在控制界限內作為判斷準則，即當|Zt|＞kσZ表明過程中存在異常原因。

2 ARMA控制圖參數的選取

在穩健設計中，信噪比指標被用以度量產品質量特性穩健程度，表達式為R=μ/s。Zhang利用信噪比定義出的檢測能力指數[5]，用來衡量過程均值發生偏移時，控制圖在各時點上檢測出偏移的能力大小。基于同樣思想我們可以根據信噪比這個指標來設定ARMA控制圖的參數,通過信噪比比值的調整來增強控制圖的檢測效能。

假設t0時刻，由于異常原因使過程{Xt}的均值由零偏移到μ，則此時點及以后各時點控制統計量Zt均值的偏移形式可由式(1)得出：

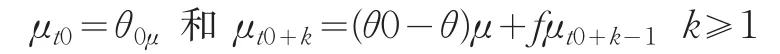
進行迭代整理后,則在t0后均值的偏移形式可統一表示為：

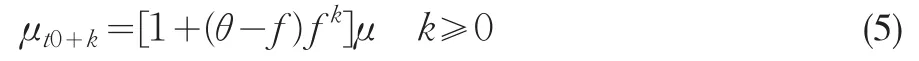
由上式可知控制統計量均值的偏移程度取決于參數θ、f和過程{Xt}均值偏移程度m，而與被監控過程的參數u和v無關。當過程{Xt}均值在時刻T=t0偏移μ個單位后，控制統計量Z的均值變化形式服從(5)式，即在時點T瞬間偏移θ0m；隨著時間t→∞，因為|φ|＜1，其在新的均衡態下偏移ms=m,則時點T和均衡狀態下的信噪比分別為：RT=μT/sZ和RS=μS/sZ。當過程{Xt}均值偏移程度統一用其標準差sx表示即m=δsx時，由(2)式可知，這兩個信噪比可寫成：

當過程均值發生偏移時，統計量Zt值位于控制限內的概率為：

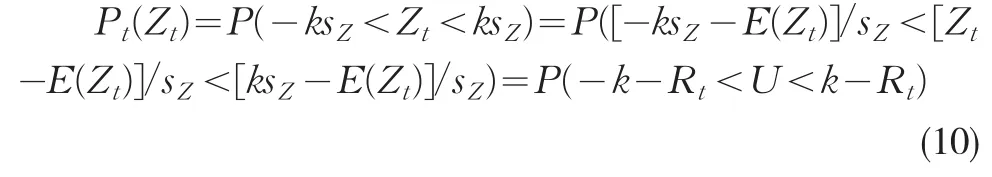
其中U為標準正態隨機變量，k通常取3。由式(10)可知，概率Pt與信噪比Rt大小有關。R值越大P值越小，則檢出概率1-P值越大，單個鏈點對異常原因的檢測能力也越大。則RT衡量ARMA控制圖在過程{Xt}均值偏移時點T的檢測能力；如果最初均值偏移未被檢出，則均衡狀態下的Rs對隨后鏈點能否有效檢測出偏移將起重要作用。因此，信噪比RT和Rs的取值決定了ARMA控制圖的檢測效能。

Jiang和Tsui總結了信噪比選取的一般原則【3】，若ARMA控制圖的RT被調到很大，這時控制圖能以較大概率在時點T迅速檢測出偏移發生，如RT=4時，由式(10)可計算出控制圖立即報警的概率約為0.8413；若RT小于3，則在異常發生初期控制圖報警的概率將小于0.5，需要用隨后的鏈點檢測，此時Rs的取值將至關重要。然而Rs不能被調得很大，因為這將會導致RT很小，控制圖及時發現異常原因的概率降低，延遲糾正錯誤的最佳時機。因此為了增強控制圖對均值偏移的檢出能力，必須選擇適宜的控制圖參數，使兩個信噪比RT和Rs達到平衡。一般來講，當Rs取值在3附近對于平衡RT和Rs是適宜的。當信噪比比值確定后，由于受控過程為平穩序列，其相關結構穩定，參數u，v不變，根據式(6)(7)相應統計量Zt的參數θ、f也就確定，具體取值則需要依據式(6)(7)和均值偏移程度計算得到的數表進行選取。在實際工作中，平穩序列的方差sx和相關系數r(k)均由樣本數據估計，為了避免自相關結構估計誤差對控制圖準確度的影響，要求樣本數據至少100個。

根據以上內容，我們總結出繪制ARMA控制圖的步驟：

（1）確定待控制的質量指標并根據實際經驗估計被測過程均值最有可能出現的偏移程度；

（2）由過程穩態下的樣本數據估計自相關模型ARMA(p,q)的參數u和v以及滯后相關系數；

（3）對 f和b（|f|＜1,|β|＜1，β=θ/θ0），根據公式(6)(7)以及第一步確定的偏移程度計算出相應RT和Rs的數表；

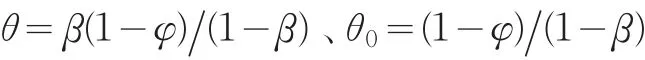
（5）計算Zt的方差與均值，繪制出控制限，作出ARMA控制圖；

（6）將測量數據在ARMA控制圖中打點，判定過程是否穩態。

3 ARMA控制圖檢測性能的比較與分析

運用Matlab軟件分別作10000次模擬運算，獲得在不同均值偏移程度下，各控制圖的ARL值，具體結果見表1。表中參數設置情況說明：第1列表示過程均值偏移程度為δ個sx單位；第2、3列是自相關過程{Xt}為ARMA(1,1)模型時的參數取值，其中at～N(0,1)；第4、5列則為ARMA控制圖相應統計量Z中參數f、θ取值，根據上節信噪比選取原則選取并由式(8)(9)計算得到。為了比較各控制圖的檢測能力，參數k取在過程穩態下使ARL大致為370的值。

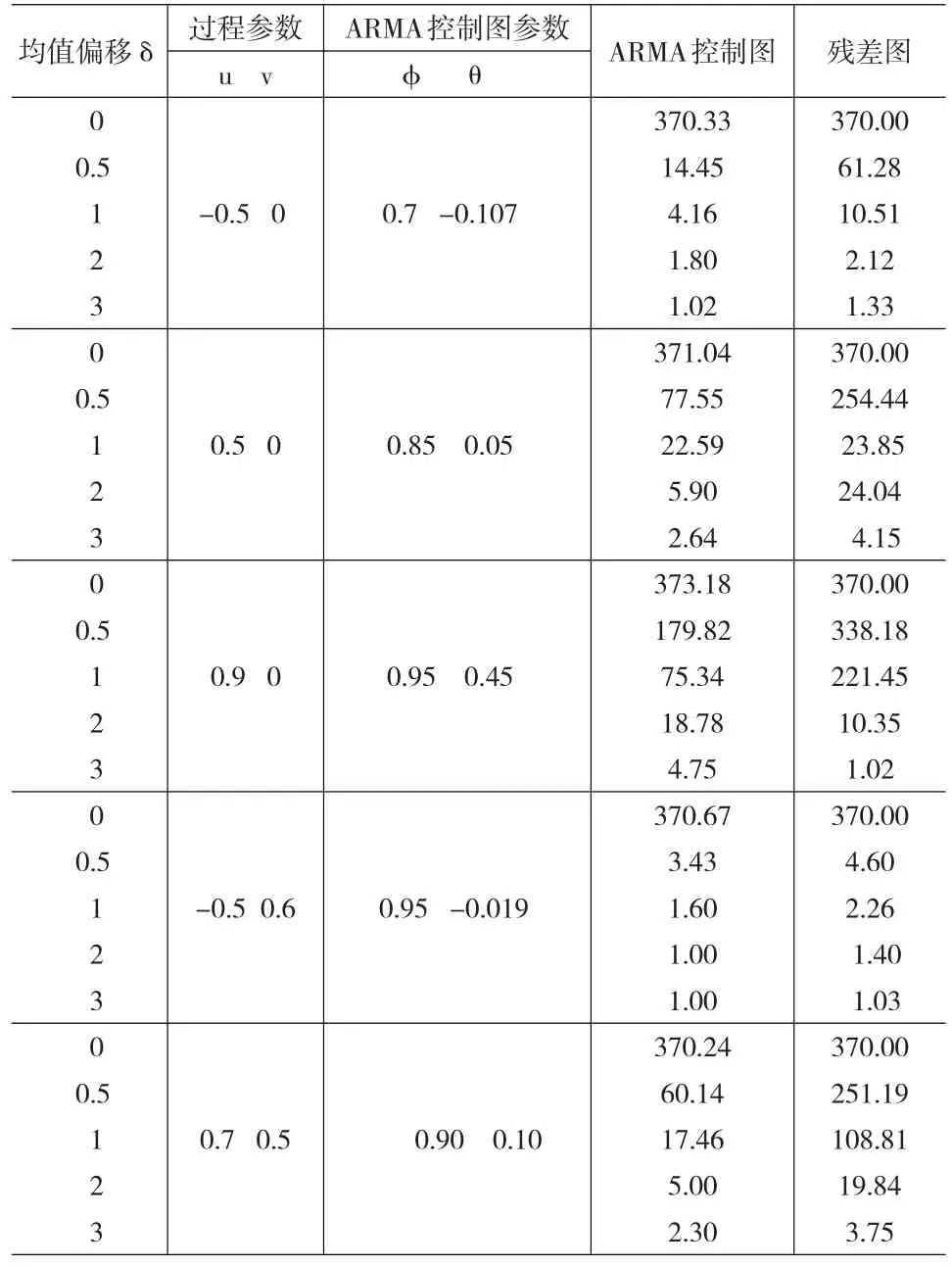
表1 自相關模型為ARMA(1，1)時兩種控制圖ARL的比較

計算結果顯示：除過程強相關且均值大偏移情況外，在絕大多數條件下，ARMA控制圖的ARL要小于殘差圖，表明其對異常原因的檢測能力較強，尤其在均值發生中小程度偏移情況更是如此。例如過程參數u=0.7,v=0.5條件下，ARMA控制圖在均值偏移程度δ=0.5，1，2時的ARL分別為60.14、17.46、5.00，明顯小于相應殘差圖的平均鏈長；而在δ=3時，ARMA控制圖的ARL也略小于殘差圖，說明此時ARMA控制圖對均值偏移的檢出能力優于殘差圖。僅在過程強相關且均值較大偏移時，ARMA控制圖的ARL要大于殘差圖，例如當u=0.9,v=0條件下，ARMA控制圖在δ=2，3的ARL分別為18.78、4.75都大于相應條件下殘差圖，表明此時檢測能力弱于殘差圖。因此，總體來講，除序列強相關且均值較大偏移情況外，通過調整ARMA控制圖中統計量Z的參數取值可以增控制圖的檢測效能。

4 ARMA控制圖的蒙特卡洛模擬研究

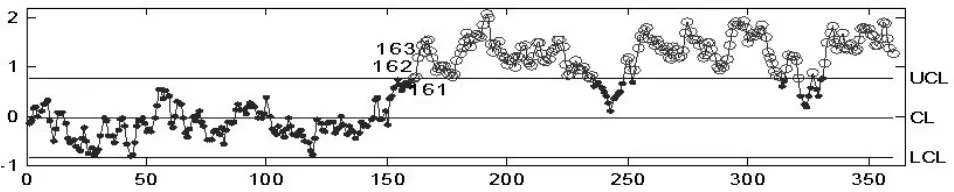
圖1 模擬數據的ARMA控制圖

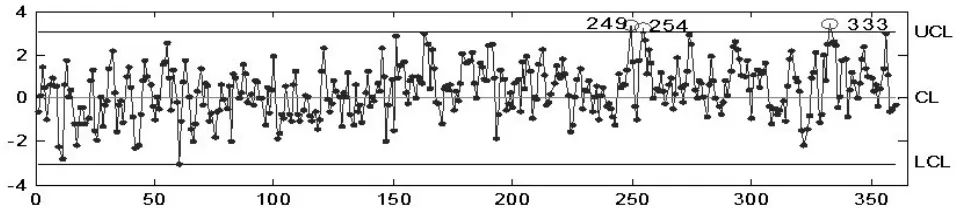
圖2 模擬數據的殘差控制圖

為了更好地理解ARMA控制圖的檢測性能，我們使用蒙特卡洛模擬方法進一步從兩個信噪比即各個鏈點檢測能力角度，研究ARMA控制圖算法對檢測效果的影響。首先，利用Matlab軟件隨機生成基于ARMA(1,1)模型Xt-0.5Xt-1=at+0.5at-1,at～N(0,1)的360個數據，其中前150個是過程穩態下的隨機數，后210個是過程均值偏移一個sx單位時的失控數據，由方差公式可計算出sx=1.5275。其次，由式(8)(9)計算出參數f和θ在取值范圍內所對應的RT和Rs的數表，根據選取原則選出適宜的信噪比RT=0.501,Rs=3.01并確定相應的f=0.95、θ=0.117，最后根據式(2)計算出控制統計量Z的方差sz，作出ARMA控制圖的控制限并對模擬序列進行控制。如圖1所示，當均值在第151個點發生偏移后，ARMA控制圖在第161個點顯示超出控制限，發出第一個報警信號，表明過程存在異常原因。對相同模擬序列用殘差圖進行控制，如圖2所示，圖中最早報警點的序號為249大大滯后于ARMA控制圖。通過模擬結果說明ARMA控制圖的檢測效果要明顯優于殘差圖，用這種控制圖方法對自相關過程進行控制是適宜的。

5 結論

建立在自回歸移動平均統計量基礎上ARMA控制圖提供了一種靈活的策略來選擇統計量參數，我們可以根據受控過程自相關結構選擇控制統計量的參數，從而通過調整兩個信噪比比值來提高ARMA控制圖檢測的靈敏度。研究結果表明除過程強相關且均值較大偏移情況外，在絕大多數條件下，ARMA控制圖檢測能力明顯優于殘差圖。因此，對自相關生產過程進行控制時，可以考慮運用ARMA控制圖來提高檢測的有效性。

[1]Alwan,L.C.,Roberts,H.V.Time-series Modeling for Statistical Process Control[J].Journal of Business and Economics Statistics,1988,6(1).

[2]王斌會,張志雷.殘差控制圖檢測能力分析及效率評價[J].統計與決策,2005，(4).

[3]Jiang Wei,Tsui K.L.A New SPC Monitoring Method:The ARMA Chart[J].Technometrics,2000,42(4).

[4]Zhang,N.F.A Statistical Control Chart for Ctationary Process Data[J].Technometrics,1998,40(1).

[5]Zhang,N.F.Detection Capability of Residual Control Chart for Station?ary Process Data[J].Journal of Applied Statistics,1997,24(2).