一種保角參數化的面積變形的優化方法

胡建平，謝 琪，左 平

(1.東北電力大學理學院，吉林 吉林132012;2.空軍航空大學 基礎部，長春130022)

曲面參數化是紋理映射、重新網格化、網格變形、網格壓縮、曲面擬合等許多數字幾何處理算法的基本工具［1］。在這些應用背景下，源于表示形式的簡單、靈活以及受各種圖形硬件廣泛支持的優點，曲面通常被表示為三角網格，它的參數化也就是通常所說的三角網格的參數化。三角網格的參數化的目標是尋求一個三角網格曲面與同它拓撲等價的簡單區域(如平面、球面等)的一一映射，通過參數化映射所得的簡單區域上的網格稱為參數網格。從數學角度來看，這樣的一一映射是很多的，尋找它并不是一件很難的事情，問題在于如何在這么多映射中找到一個相對比較“好”的映射?人們通常使用曲面的一些諸如角度、面積、長度等幾何內在的屬性的變形程度來衡量三角網格參數化的好壞［2］。

由于任意復雜的模型都可以切割成很多同胚于圓盤的區域，將它們分別參數化到平面上即可完成對整個模型的參數化。因此，三角網格平面參數化是網格參數化迄今為止研究得最多的話題。曲面參數化早期被引入到計算機圖形學的應用—紋理映射也是以平面參數化為基礎的。對于任何同胚于圓盤的可定向的光滑的二維流形曲面來說，黎曼映射定理保證了保角的平面參數化總是存在的。但是對于三角網格來說，黎曼映射定理并不一定成立。在實際計算中，通常是最小化與網格角度變形相關的度量來得到保角參數化。現有的保角參數化方法按照最小化與網格角度變形相關的度量的種類可以分為固定凸邊界的方法、基于圓模式的方法以及基于角度展平的方法等［3］。由于保角參數化在能量最小化時沒有考慮到原始網格曲面的面積屬性，因此對于具有復雜結構的三角網格通常會產生比較大的面積變形，一定程度上影響了其在紋理映射、重新網格化等數字幾何處理的應用。

針對此類問題，本文提出了一種優化方法，該方法通過引入保角參數網格頂點的平均值坐標權和面積變形因子對保角參數化進行優化。通過典型的三角網格模型的實驗比較可以看出，本文方法所得的參數化的面積變形較保角參數化有明顯改善，同時角度變形接近于保角參數化。

1 優化方法

三角網格模型M可以表示為一個二元組(V，K)，其中V表示網格中頂點的集合{vi∈R3}，K是一個單純復型，包含M中所有拓撲連接關系的集合。K里面的元素有三種類型:頂點{i}，邊{i，j}和面{i，j，k}。我們記K中邊的集合為E，面的集合為F。如果{i，j}∈E，則稱頂點{i}和頂點{j}是鄰居。頂點{i}的1 環鄰居被定義為 N(i)={j|{i，j}∈ E}，它的星形鄰域被定義為 Star(i)= ∪i∈s，s∈Ks。如果頂點{i}的星形鄰域在網格中對應的區域同胚于圓盤(半圓盤)，則該點稱為內部頂點(邊界頂點)。

設M在平面區域的保角參數網格為P，可以通過固定凸邊界的方法［4］、基于圓模式的方法［5］等得到(圖1)。本文提出的優化方法是將保角參數網格P的邊界頂點固定，然后通過求解一個線性方程組得到內部頂點在平面上的對應頂點ui。該線性方程組是通過保角參數網格頂點的平均值坐標權和面積變形因子得到。它的具體形式如下:

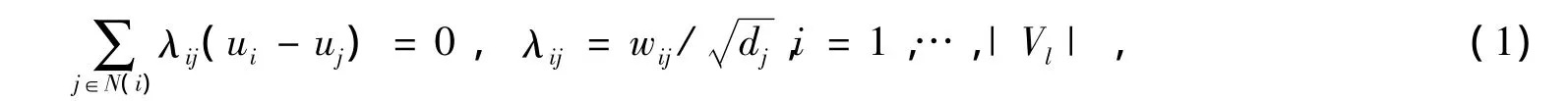
式中uj表示頂點vi的一環鄰點vj在平面上對應的頂點，wij和dj分別表示頂點在保角參數網格P中對應頂點pj的平均值坐標權和面積變形因子，|Vl|表示三角網格中的內部頂點的數目。

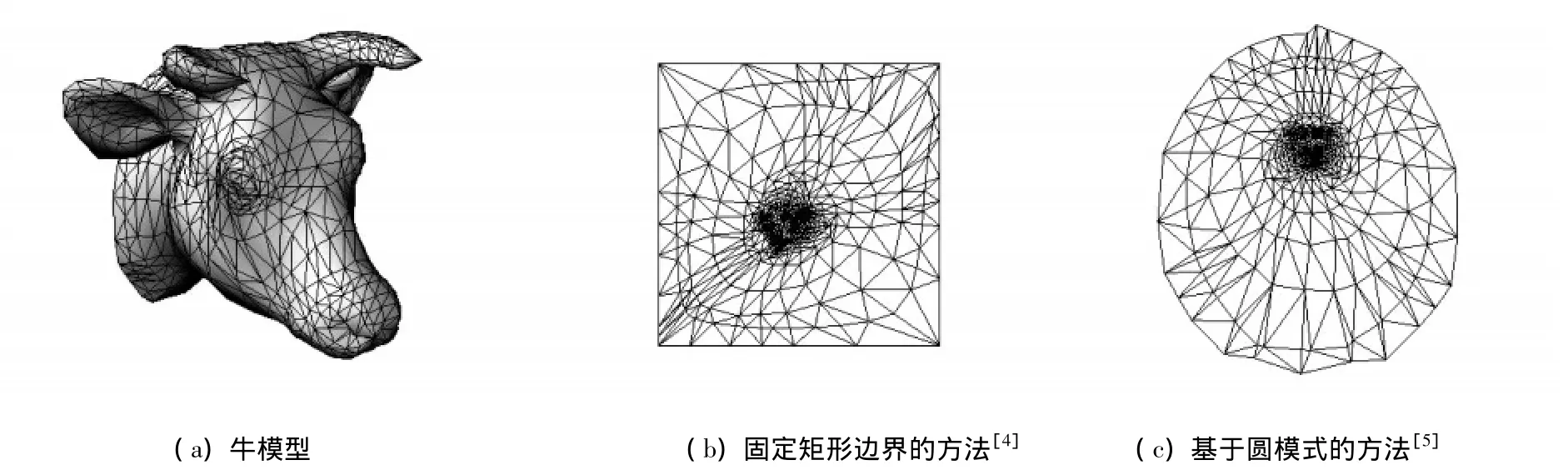
圖1 通過不同的方法得到的保角參數化網格

平均值坐標權是通過調和映射滿足平均值定理得出來的［4］。由于調和映射是通過最小化離散的Dirichlet能量得到的，因此平均值坐標權可以減少參數化的角度變形。它的計算公式如下:

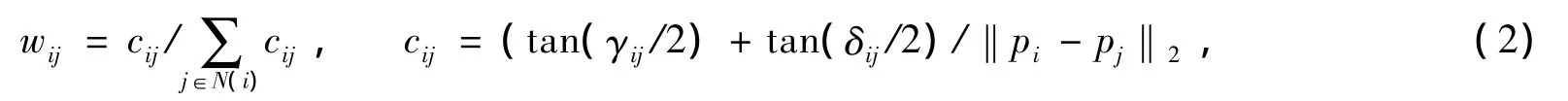
其中pi，pj分別表示保角參數網格P的一條邊的兩個頂點，γij，δij表示該邊與相鄰頂點形成的角度(圖2)。

保角參數網格頂點的面積變形因子可通過三角形的面積變形進行計算。對于保角參數網格的一個三角形U，它的面積變形定義為它在原始網格中所對應三角形T同它的面積之比，即:

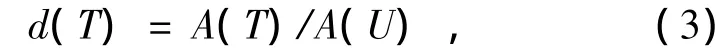
式中A(·)表示三角形的面積。則每個頂點pi的面積變形di就可定義為它在原始網格中對應頂點vi的一環相鄰三角形Tj的面積變形的加權平均，即為:

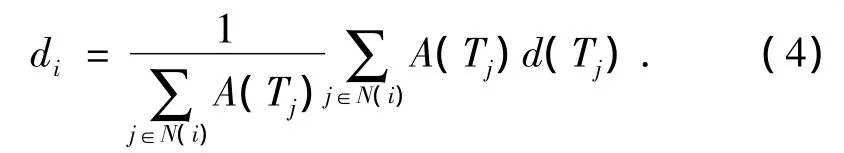
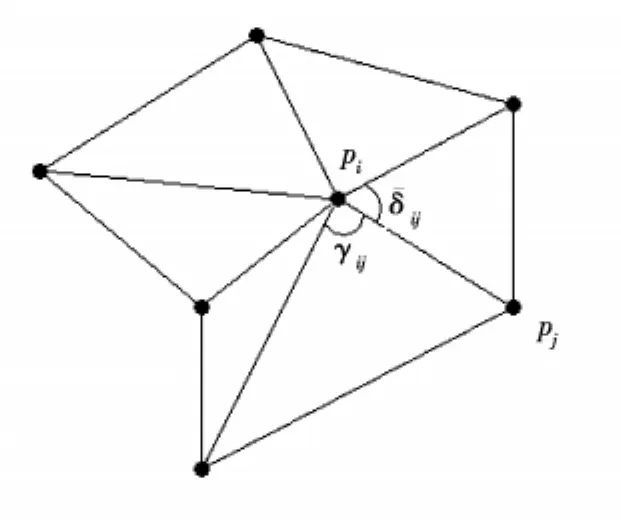
圖2 平均值坐標權的計算

這種優化方法的本質是通過引入平均值坐標權控制優化參數化角度變形，同時對面積變形比較大的頂點對平均值坐標權進行縮放，即采用較小的權值，使得該頂點朝面積變形較小的區域移動，從而減少保角參數化的面積變形。優化時以頂點的面積變形的平方根進行縮放，控制了面積變形比較大的頂點移動的距離，使得優化后的參數化的角度變形不至于發生太大的變化。

2 實驗結果分析和討論

通過將原始網格的法向量映射到參數區域，或者將參數區域上棋盤等紋理映射到原始網格上的視覺效果是衡量參數化變形的一個直觀標準;除此之外，還可以通過參數網格與原始網格之間的面積相對誤差和角度相對誤差等測度來衡量參數化的面積和角度變形程度，它們的計算公式如下:

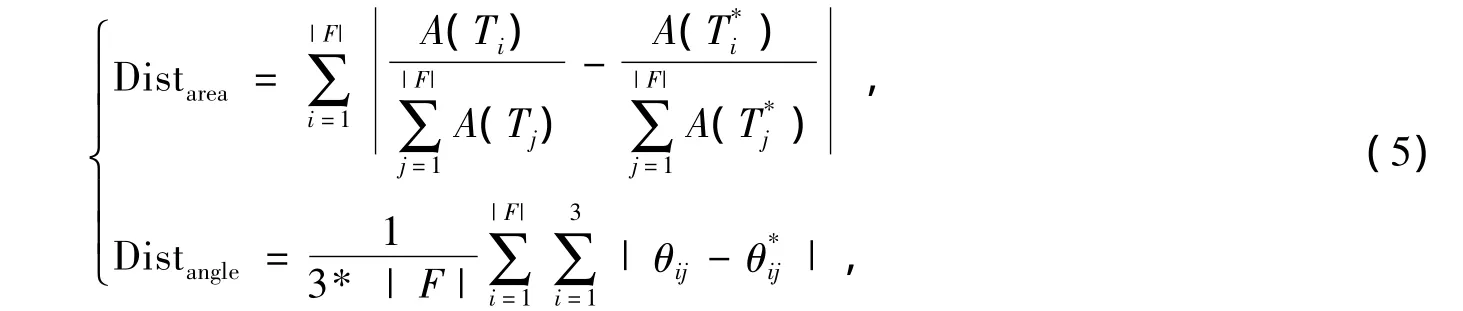
其中|F|表示原始網格M的三角形數目，A(Ti)表示網格M的第i個三角形Ti的面積，A()表示參數網格中與Ti所對應的三角形的面積，θij表示網格M中三角形Ti的第j個角度表示參數網格中θij與對應的角度。

為了檢驗本文優化方法的有效性，我們選用了幾種典型的三角網格模型如貓、手、人頭、牛頭模型(手和牛頭模型具有細長的結構)進行測試，通過固定矩形邊界的方法［4］和基于圓模式的方法［5］所得的保角參數化作為初始輸入進行優化，給出了原始網格的法向量映射到優化前后的參數網格的效果圖，以及優化前后參數化的角度和面積變形統計，如圖3、圖4、表1所示。通過這些比較可以看出，本文方法所得的參數化的角度變形接近于初始輸入的保角參數化，但是面積變形明顯減少。

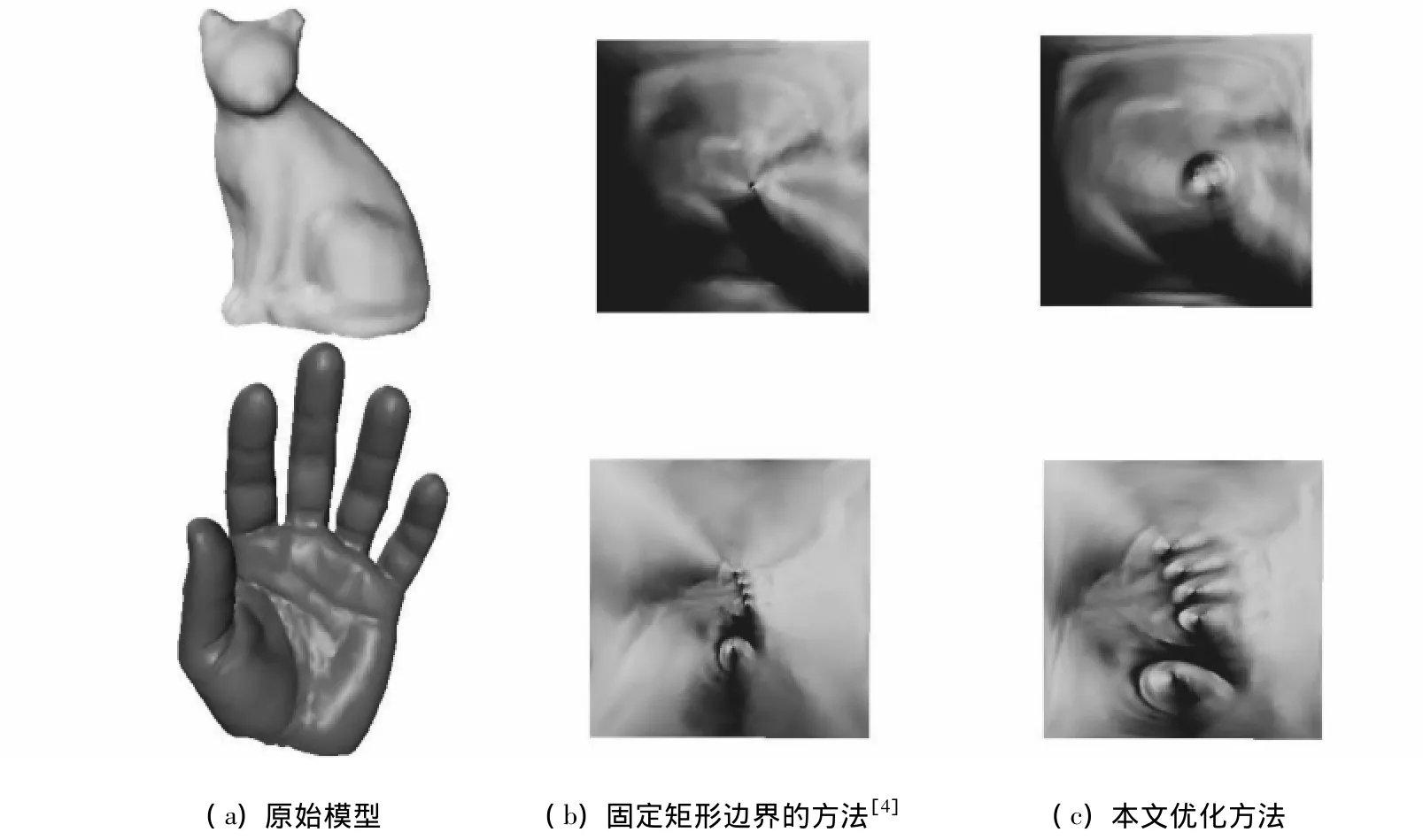
圖3 參數化結果比較

表1 一些典型模型參數化變形統計比較

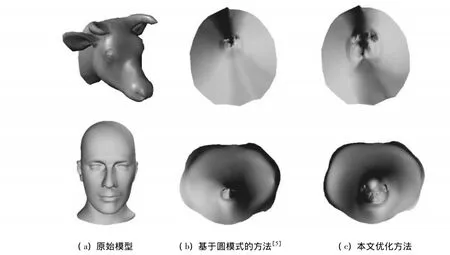
圖4 參數化結果比較

3 結論和未來工作

本文通過引入保角參數網格的平均值坐標權和頂點的面積變形因子對保角參數化進行優化，明顯減少了復雜結構物體的保角參數化的面積變形，在紋理映射、重新網格化、網格變形等數字幾何處理的應用中具有重要的價值。在未來的研究中，我們打算將本文的參數化方法應用在紋理映射、重新網格化、網格變形等數字幾何處理的應用中。

［1］Sheffer，A.，Praun，E.，Rose K.Mesh Parameterization Methods and their Applications［J］.Computer Graphics and Vision，2006，2(2):105-171.

［2］彭群生，胡國飛.三角網格的參數化［J］.計算機輔助設計與圖形學學報，2004，16(6):731-739.

［3］胡建平.數字幾何處理中球面參數化和重新網格化研究［D］.遼寧:大連理工大學，2009.

［4］Floater，M.S.Mean value coordinates［J］.Computer Aided Geometric Design.2003，20(1):19-27.

［5］Kharevych，L.，Springborn，B.，Schr?der，P.Discrete conformal mappings via circle patterns［J］.ACM Transactions on Graphics.2006，25(2):412-438.