發電機組污染排放約束下電量互換合作博弈優化模型

譚忠富 董力通 劉文彥 于 超 宋藝航

（華北電力大學經濟與管理學院 北京 102206）

1 引言

我國是世界第二大能源消費國，隨著經濟快速發展和人民用電水平提高，我國的用電需求增幅明顯，能源供應形勢日趨緊張。在能源消耗巨幅增加的同時，也帶來了一系列環境污染問題。在我國所排放的污染物中，發電企業的排放量占了很大的比重，發電廠所排放的污染物主要有二氧化硫、氮氧化物、粉塵、廢水及固體廢物，其中二氧化硫的排放達到了全社會總排量的一半，固體廢物的生產量占工業固體廢物產生量的20%左右。

近年來我國對污染排放嚴重的火力發電企業頒布了多項節能減排政策。1996年、2003年兩次頒布了《火電廠大氣污染物排放標準》，提出了燃煤電廠煙塵、二氧化硫、氮氧化物的排放標準。2003年頒布的《排污費征收使用管理條例》，對各種污染的收費都進行了明確的規定。在2009年的世界氣候大會上，我國承諾到2020年單位GDP 碳排放比2005年減少40%～45%[1]。作為工業污染排放大戶的電力企業，其污染排放控制效果將直接決定我國減排目標的實現。

發電節能調度是實現火力發電企業節能減排的重要手段，目前已在河南、貴州、四川等省份開展了試點工作。而關于節能調度的研究大多圍繞機組組合的節能效果開展，如文獻[2]考慮了環境成本、阻塞成本、煤耗以及網絡約束，分別以社會效益最大、環境成本最小為目標函數，建立了水火電廠間的發電權交易模型。文獻[3]利用二氧化碳的排放量函數代替能耗函數，設計了考慮電力市場與節能調度相互協調的機組組合模型。文獻[4]論述了節能調度下兼顧環境保護和經濟效益的多目標混合電力系統發電計劃模型，提出在節能調度下風、水、火電混合系統的中長期發電計劃模型。文獻[5]將粗糙集模型應用到河北南網的發電節能調度優化過程中，選出對實現節能降耗有較大影響的指標，對指標進行分析，提出相應的節能降耗措施。文獻[6]建立了系統有功網損最小和機組發電耗煤量最小的多目標負荷分配模型。該模型改進了基于Pareto 最優概念的多目標粒子群算法，將其應用于多目標負荷最優分配，能對系統進行整體節能優化。從上述文獻分析可以看出，已有的文獻多是對于節能調度下機組組合的方法和節能效果進行優化，而對于節能調度下機組組合帶來的利益分配卻無探討，本文將污染排放懲罰成本引入到傳統的發電經濟調度模型中，構建了污染排放成本與發電成本最小化下的合同發電量置換優化模型，并采用合作博弈利益分配的Shapley 模型對合作后所有機組之間利潤進行優化分配。

2 發電經濟調度優化模型

發電經濟調度是指在滿足電力系統安全運行及電能質量的前提下，利用資源與設備，以發電成本最小化為目的進行的發電量的轉移。在發電經濟調度的過程中，需要滿足多個約束，調度的最終結果是發電機組之間電量的重新分配，達到整體的成本最小化。

現假設在某一時段內參與發電經濟調度的機組有n臺，該時段又被分為T段時間，則目標可以表示為

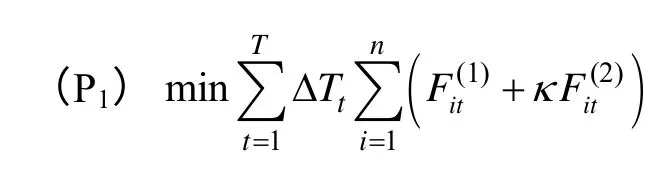
式中，ΔTt為時間段長度，為了討論上的方便，后面取ΔTt=1，于是可以不再出現；是第i臺機組T時間段內的運行成本，這里假設函數關系為；是機組i在T時段內污染物（CO2、NOx）排放量，這里假設函數關系為，κ指發電排放物（CO2、NOx）的單位懲罰費用或者排放稅；git是機組i時刻t的出力。

約束條件是：

（1）每個時段所有機組的發電量總和是額定值，記為tD

（2）在相鄰時段之間，機組i的發電爬坡速度受到限制

（3）機組i在ΔtT時段內的發電量受到上、下限約束，gimin、gimax是機組i的最小、最大出力限制

（4）機組i的排放污染物總量的限制，2maxiF指機組i在T時段內發電排放物（CO2、NOx）的最大限制

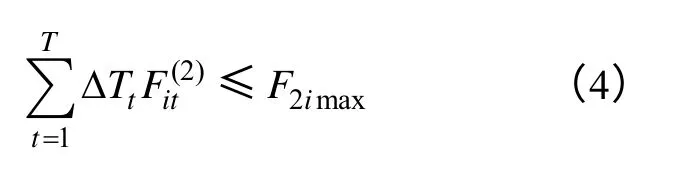
（5）機組i在所有時段內的發電量總和不能低于合同電量Qci

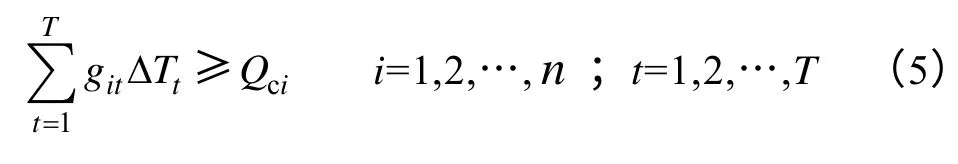
3 發電機組電量互換合作博弈優化模型及利益分配

合作博弈也稱為正和博弈，是指博弈雙方的利益都有所增加，或者至少是一方的利益增加，而另一方的利益不受損害，因而整體利益增加。合作博弈主要是研究利益的分配問題，因為合作博弈能夠產生一種合作剩余，這里所采用的shapley 法就是一種合作博弈模型。

將一組參與者定義為集合N={1,2,…,n}，V(S)是N的任意一子集S所對應的函數值，在這里被視為合作者通過合作獲得的利益，并且滿足條件，V(φ)=0，V(S1∪S2)+V(S1∩S2)≥V(S1)+V(S2)，本文中各個廠商之間是相互獨立的，所以條件可以寫為V(S1∪S2)≥V(S1)+V(S2)，則稱[N,V]為n人合作對策，V為對策的特征函數。用Xi表示N中第i個成員從合作的最大效益值V(N)中應得到的一份收入，則X=(X1,X2,…,Xn)稱為合作博弈對策的分配策略。

如果X滿足如下3 個特性：

（2）個體合理性：Xi≥V(i)，?i∈N，其中V(i)是成員i不與其他成員結盟時的收益；

則稱分配X為該合作博弈的核，記為C(V)。合作博弈的核可能是空集，也可能是多解。目前解決合作利益分配問題的有效方法是Shapley 值法。

Shapley 值指滿足以下3 個公理：

（1）有效性。若成員i對其所參與的合作沒有貢獻，那么就不應對其進行分配，且所有成員的收益總和等于總收益。可以表達為當V(S-i)=V(S)時，則有

（2）對稱性。每一個合作組合中，成員所得利益分配與其記號無關。令π是N={1,2,…,n}的一個排列，若πi為i的對應，πs為S的對應（S?N）；記V(πs)=U(S)，則對于一切i=1,2,…,n有X πi(V)=X i(U)。

（3）可加性。對于集合N上的任意兩個特征函數U和V，有X i(U+V)=X i(U)+X i(V)，i=1,2,…,n。即n人同時進行兩項合作時，該收益應該為兩項合作的分配之和。

針對Shapley 值，Shapley 給出了計算合作對策利益分配的模型。

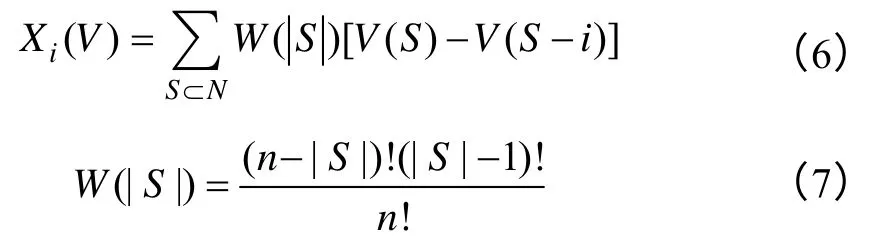
Shapley 值由特征函數V確定，合作博弈的分配策略Xi表達為 式中，S是包含i的所有子集；|S|是子集S中的元素個數；W(|S|)是加權因子；V(S)是包含i的聯盟S的合作收益；V(S-i)是不包含i的聯盟收益，N={1,2,…,n}，i=1,2,…,n。

記I為機組之間在合同電量、排污約束聯盟方面的各種方案的集合：I={I1,I2,…,Im}，即存在如下的各種聯盟方式：

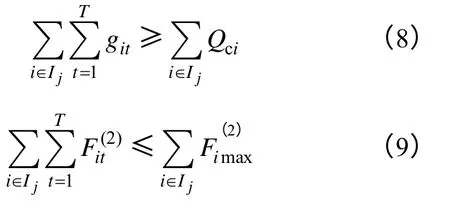
針對每一種聯盟方式Ij，分別計算：

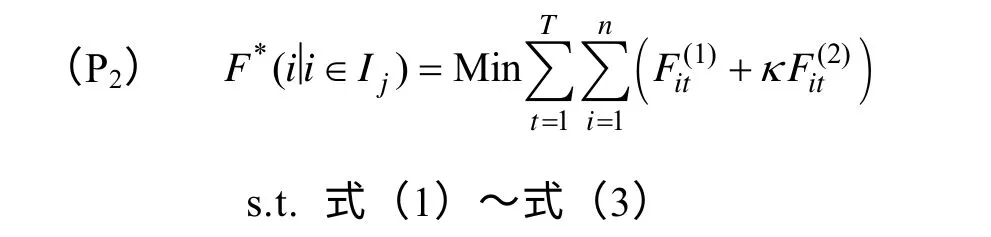
對于ji I∈，git需要滿足式（8）和式（9）；對于ji I?，git需要滿足式（4）和式（5）。

在此基礎上，首先計算Ij聯盟后，所有發電機組的利潤總和

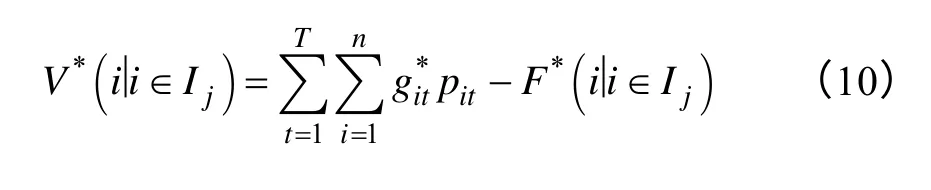
接著計算所有發電機組進行聯盟后的利潤總和：

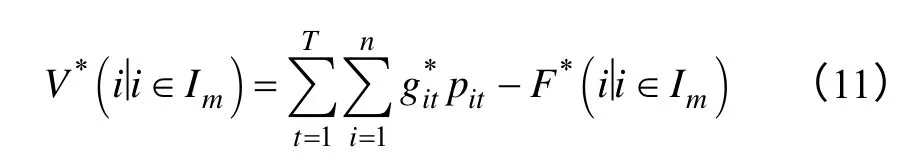
式中，Im={1,2,…,n}。

然后計算，所有發電機組進行聯盟后，每臺發電機組分配的利潤為

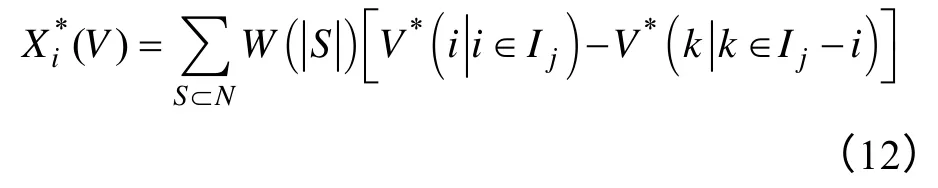
式中，W計算見式（7）。

最后計算，所有發電機組進行聯盟后的發電成本與排污成本：

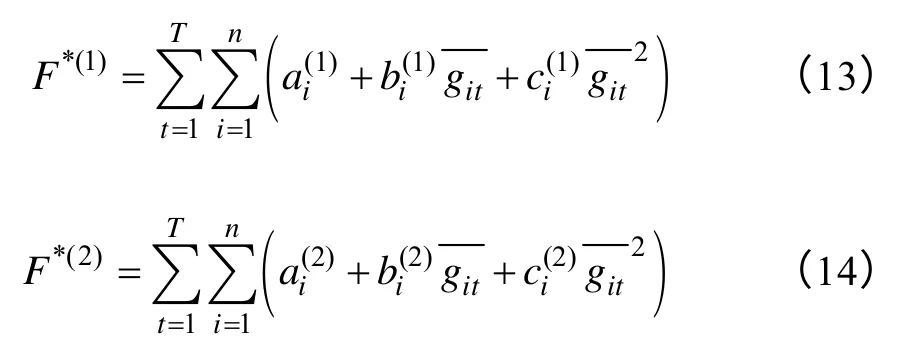
為了更容易理解上述模型，下面針對3 臺機組的情況進行具體分析：

（P3）minF*（1,2,3）

s.t.式（1）～式（3）

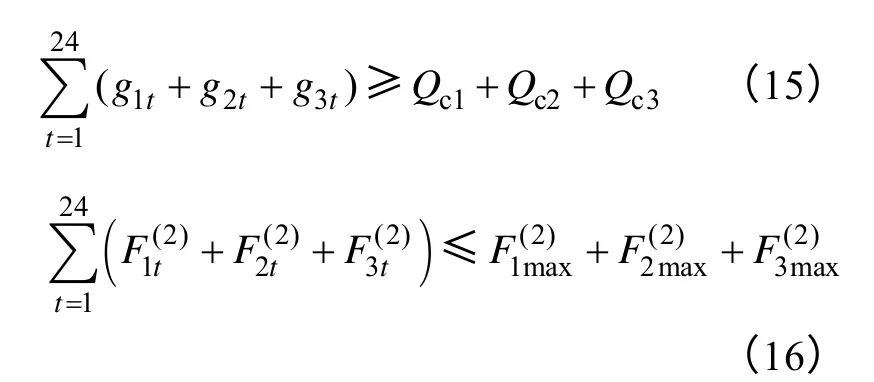
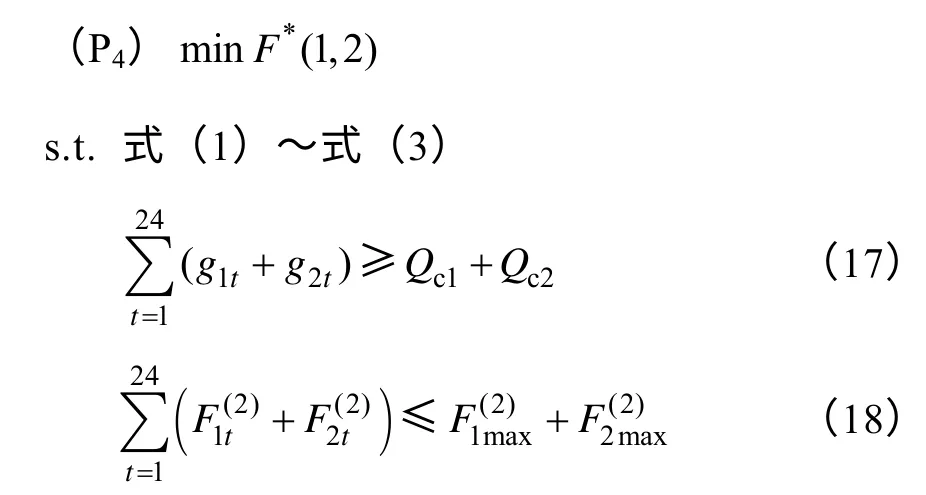
得到V*（1 ,2）。

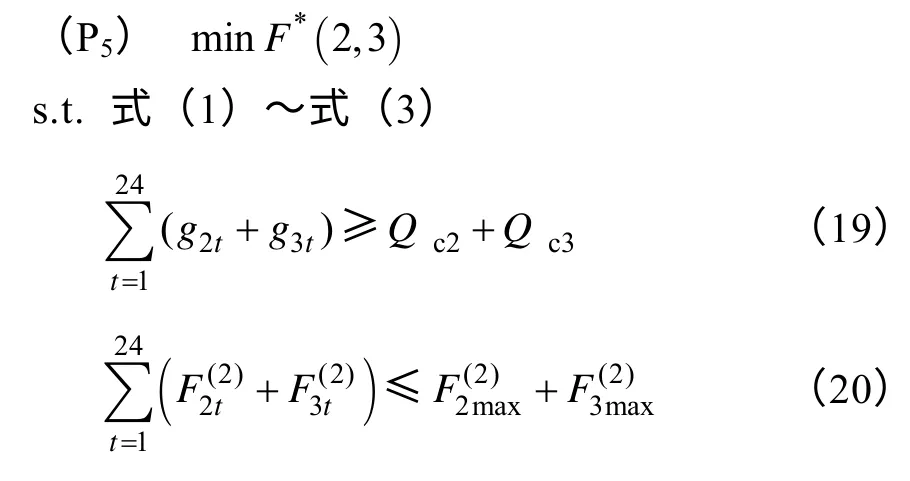
得到V*（2,3）。

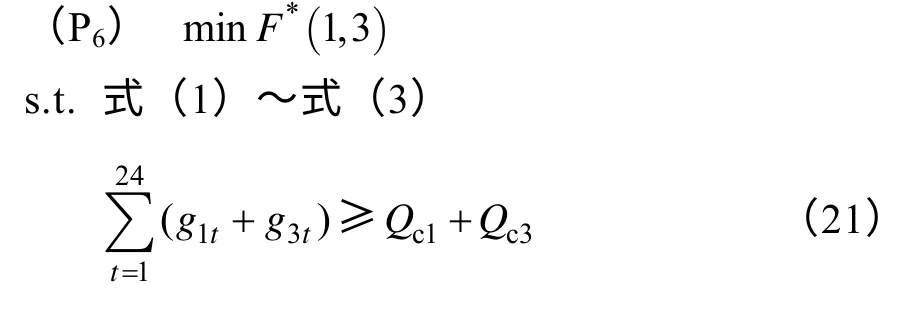
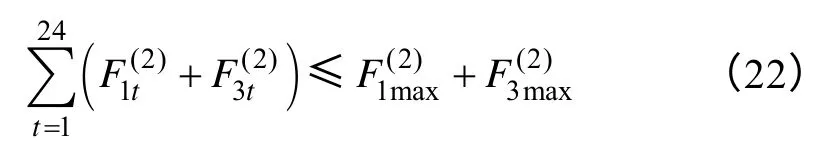
得到*(1,3)V。

機組1 本身獨自參加聯盟情形下，由于沒有合作者，等于沒有聯盟，故（見式（6））。同理，可以得到：

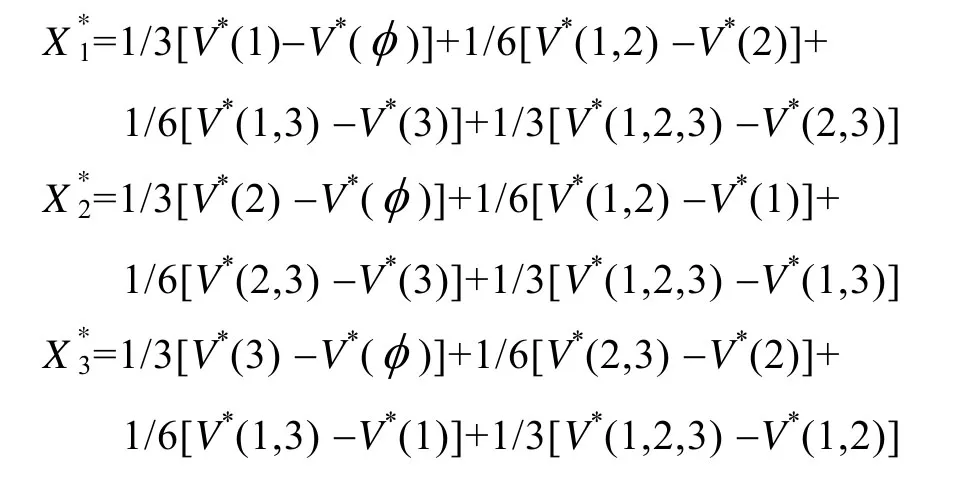
4 算例

假設現有3 臺機組，令T=24h，運用Matlab 進行優化計算。已知 3 臺機組的裝機容量分別為300MW，600MW，1 000MW，3 臺機組的運行成本參數、排污量參數，運行出力的上下限值，每個時段出力允許變化的幅度，每臺機組的合同電量信息見表1。三臺機組的排污允許總量為4 萬t，κ取0.02元/kg，即20 元/t。

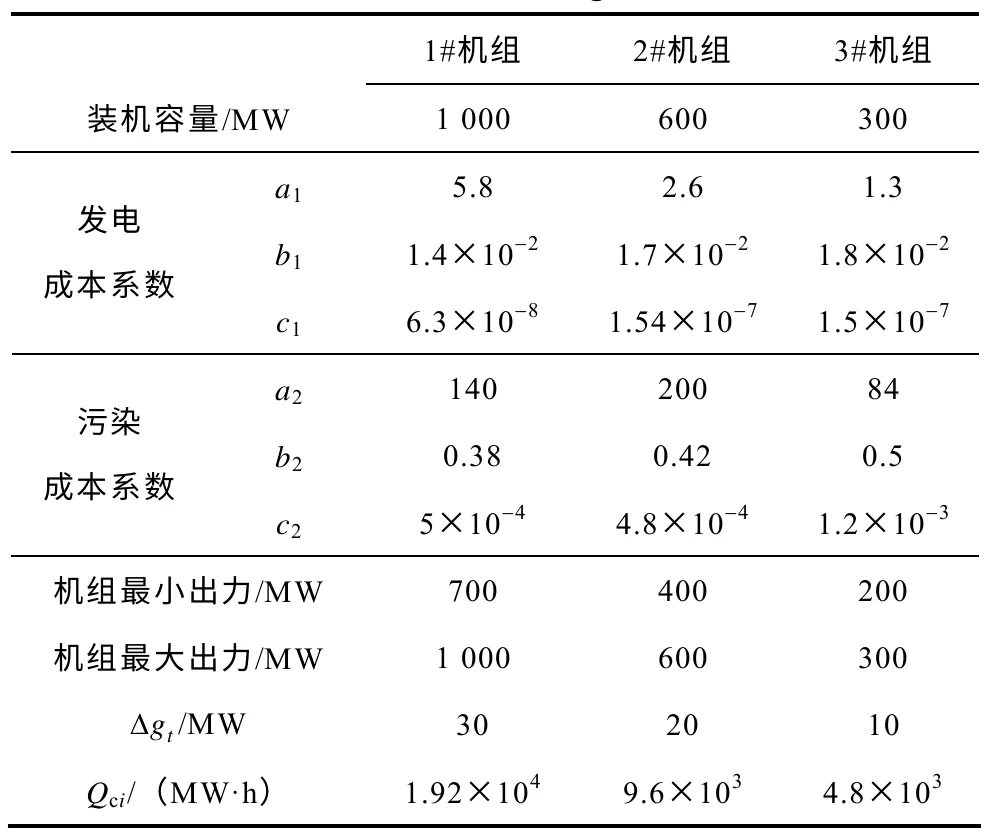
表1 發電機組參數Tab.1 Parameter of generators

當未進行發電量的置換而分配發電量時，3 臺機組各自的發電量是用每個時段的總發電量乘以該機組裝機容量占總裝機容量的比重來決定的，這里沒有機組間的電量置換，每個時段的發電量、各臺機組的發電量、總的發電量見表2。

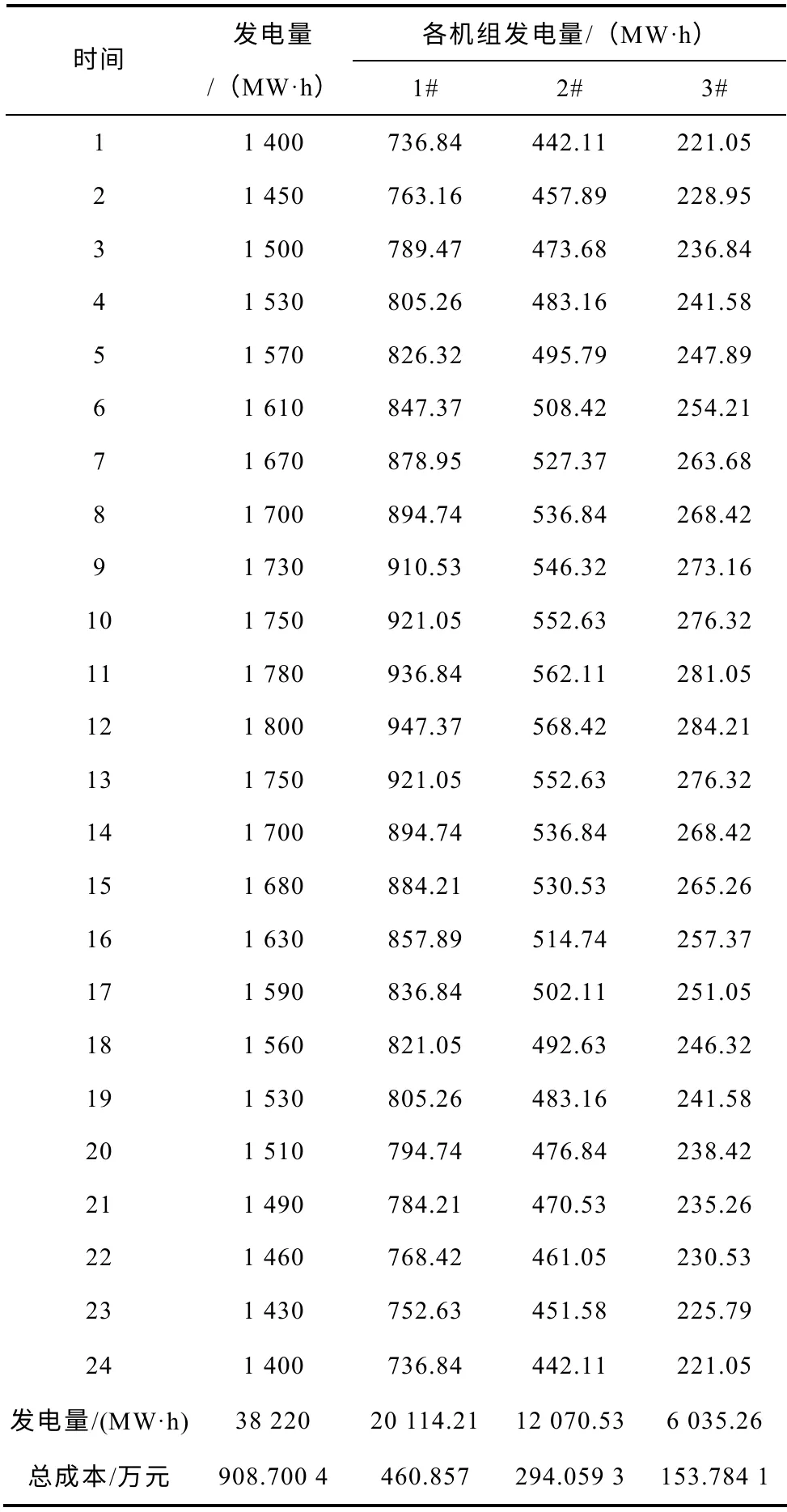
表2 機組間發電置換前的調度結果Tab.2 Power output before generation replacement

假設三臺機組的上網電價都是相同的且不變，均為0.3 元/(kW·h)，根據機組的發電量可以確定機組各自的利潤及總利潤，見表3。

表3 機組間置換前的發電利潤Tab.3 Generation profits before generation replacement

當考慮了污染函數后，重新對這3 臺機組進行電量分配的優化求解，優化后的結果，各個機組的發電量、排污總量均滿足約束條件，結果見表4。

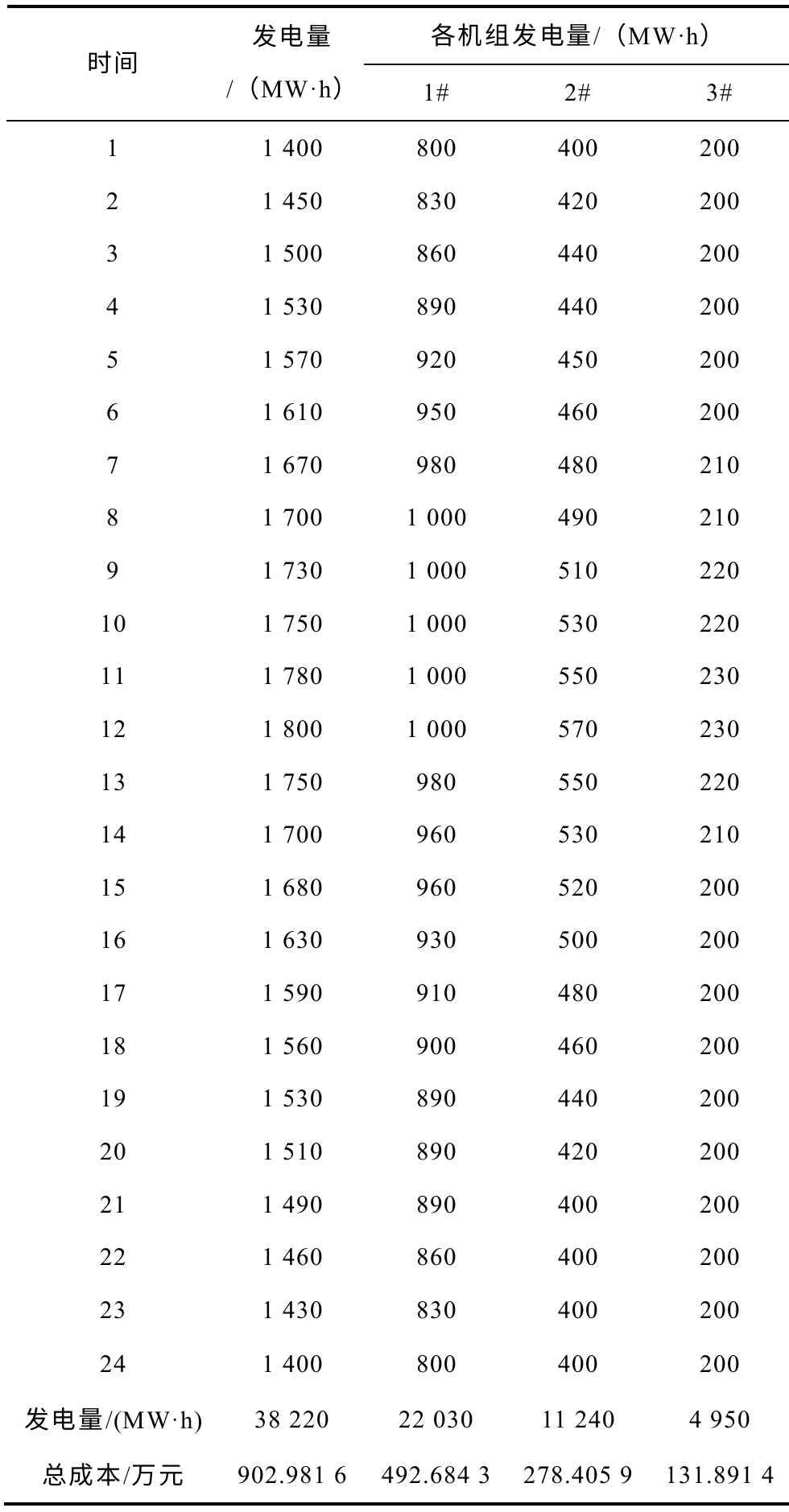
表4 機組間發電置換后的調度結果Tab.4 Power output after generation replacement

可以計算出考慮污染成本后機組之間的利潤，見表5。

表5 機組間電量置換后利潤Tab.5 Generation profits after generation replacement

根據所給出的Shapley 法，對3 臺機組之間的合作組合進行了計算，分別得出了V*(1,2,3)，V*(1,2)，V*(2,3)，V*(1,3)，根據這些組合的結果得到了Shapley 法的最終結果，見表6。

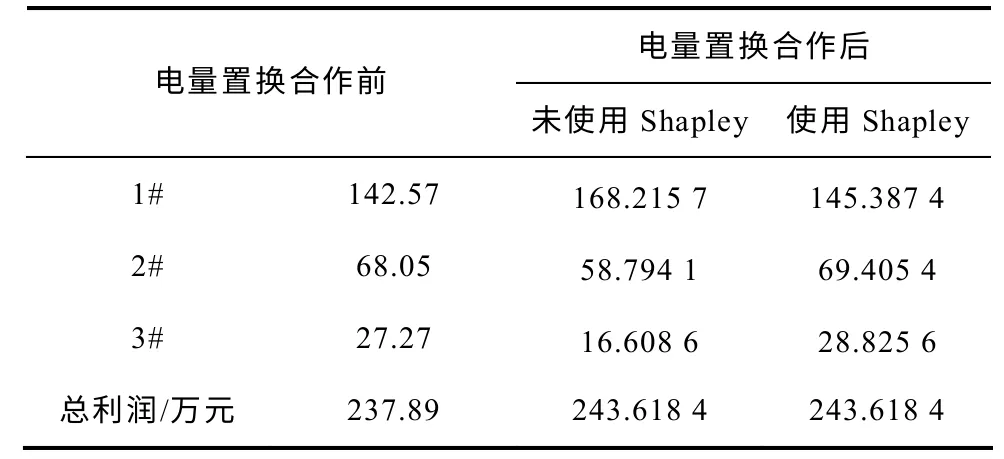
表6 機組間合作前后利潤分配結果對比Tab.6 Profits distribution results of units cooperation

通過計算，發現發電量從總成本高的機組轉移到了成本低的機組上，2 號機組共轉移了830.53MW·h的電量到1 號機組上，3 號機組共轉移了1 085.26MW·h的電量到1 號機組上，這使得三臺機組的利潤發生了變化，1 號機組的利潤增加了25.65 萬元，2、3 號機組的利潤一共減少19.92 萬元，三臺機組的總利潤增加了5.73 萬元，這說明發電量的置換對整體有益。當運用Shapley 法對所得收益進行分配后，三臺機組與未進行合作時相比分別增加了2.82、1.36、1.55 萬元，合作為三臺機組都帶來了利益的增加。

5 結論

本文在考慮機組污染成本的前提下進行機組發電量的置換，這是一種合作的方式。本文首先建立了考慮污染成本情況下的置換優化模型，然后運用合作博弈模型對合作的盈利進行了分配，使參與的各方的收益都有所增加，通過分析可以得出以下結論：

（1）在成本導向的前提下，通過合作進行的電量置換可以減少總體運營成本，使發電企業獲取更多利潤。

（2）在降低成本的同時，污染物的排放也會相應減少，該機制不僅促進了機組節能減排積極性，還推動了高能耗、高污染機組退出市場。

[1]中華人民共和國國務院新聞辦公室.中國的環境保護(1996－2005).www.gov.cn/zwgk/2006-06/05/content_ 300288.htm.

[2]陳赟,嚴正.考慮節能減排與網絡約束的發電權交易模型[J].電力系統保護與控制,2009,37(12):52-57.Chen Yun,Yan Zheng.Generation rights trade model based on energy-saving,emission-reducing and network constraint[J].Power System Protection and Control,2009,37(12):52-57.

[3]徐致遠,羅先覺,牛濤.綜合考慮電力市場與節能調度的火電機組組合方案[J].電力系統自動化,2009,33(22):14-17.Xu Zhiyuan,Luo Xianjue,Niu Tao.Thermal unit commitment scheme considering electricity market and energy-saving dispatch[J].Automation of Electric Power Systems,2009,33(22):14-17.

[4]溫麗麗,劉俊勇.混合系統中、長期節能調度發電計劃的蒙特卡羅模擬[J].電力系統保護與控制,2008,36(24):24-29.Wen Lili,Liu Junyong.Monte Carlo simulation of medium and long-term generation plan in hybrid power system based on environmental/economic dispatch[J].Power System Protection and Control,2008,36(24):24-29.

[5]鄒穎.河北南網發電節能調度優化研究[D].保定：華北電力大學(河北),2007.

[6]蘇鵬,劉天琪,趙國波,等 基于改進粒子群算法的節能調度下多目標負荷最優分配[J].電網技術,2009,33(5):48-53.Su Peng,Liu Tianqi,Zhao Guobo,et al.An improved particle swarm optimization based multi-objective load dispatch under energy conservation dispatching[J].Power System Technology,2009,33(5):48-53.

[7]Li Shujin,Zhang Qiang.A simplified expression of the Shapley function for fuzzy game[J].European Journal of Operational Research,2009,196(1):234-245.

[8]喻潔,李方興,李揚,等.互聯區域多目標發電調度的協同優化策略[J].電力系統自動化,2009,33(2):30-33.Yu Jie,Li Fangxing,Li Yang,et al.A coordinated optimization strategy for multi-objective generation dispatch in interconnected areas[J].Automation of Electric Power Systems,2009,33(2):30-33.

[9]謝國輝,張粒子,邵志剛,等.改進Shapley 值在協同報價利潤分配中的應用[J].華東電力,2009,37(2):232-235.Xie Guohui,Zhang Lizi,Shao Zhigang,et al.Application of improved Shapley value to profit distribution for collaborative bidding[J].East China Electric Power,2009,37(2):232-235.

[10]譚忠富,陳廣娟,趙建保,等.以節能調度為導向的發電側與售電側峰谷分時電價聯合優化模型[J].中國電機工程學報,2009,29(1):55-60.Tan Zhongfu,Chen Guangjuan,Zhao Jianbao,et al.Optimization model for designing peak-valley time-of-use power price of generation side and sale side at the direction of energy conservation dispatch[J].Proceedings of the CSEE,2009,29(1):55-60.

[11]Abido M A.Environmental/economic power dispatch using multi-objective evolutionary algorithms[J].IEEE Transactions on Power Systems,2003,18(4):1529-1536.

[12]尚金成.基于節能減排的發電權交易理論及應用(一)發電權交易理論[J].電力系統自動化,2009,33(12):46-52.Shang Jincheng.Generation right exchange theory and its applications based on energy-saving and emission-reducing part one generation right exchange theory[J].Automation of Electric Power Systems,2009,33(12):46-52.

[13]喻潔,李揚,夏安邦.兼顧環境保護與經濟效益的發電調度分布式優化策略[J].中國電機工程學報,2009,29(16):63-68.Yu Jie,Li Yang,Xia Anbang.Distributed optimization of generation dispatch schedule considering environmental protection and economic profits[J].Proceedings of the CSEE,2009,29(16):63-68.

[14]彭春華.綜合環境保護及競價風險的發電側經濟運行[J].中國電機工程學報,2008,28(28):97-102.Peng Chunhua.Economic operation problem of generating side considering environmental protection and bidding risk[J].Proceedings of the CSEE,2008,28(28):97-102.

[15]譚忠富,李莉,王建軍,等.多智能體代理下電力雙邊談判中的模糊貝葉斯學習模型[J].中國電機工程學報,2009,29(7):106-113.Tan Zhongfu,Li Li,Wang Jianjun,et al.A fuzzy bayesian learning model in agent-based electric power bilateral negotiation[J].Proceedings of the CSEE,2009,29(7):106-113.