基于多時段同步測量信息的T接線路參數在線測量

牛勝鎖 梁志瑞 張建華 蘇海鋒

（華北電力大學新能源電力系統國家重點實驗室 保定 071003）

1 引言

線路參數通常采用設計值或經驗值。由于部分線路的設計運行條件與實際運行條件之間存在差別，且元件自身也在局部、緩慢地變化，因此線路參數的設計值與真實值之間可能存在較大的差值。電力系統狀態估計、潮流計算、網損分析和繼電保護整定計算等都要求線路參數足夠準確，因此，提高線路參數測量的準確性對電網的安全穩定運行具有重大意義。

隨著廣域測量系統（Wide Area Measurement System，WAMS）在電力系統應用越來越廣泛，基于線路兩端同步測量信息的線路參數在線測量取得了一定發展[1-4]，另外，一些具有同步測量功能的電能質量監測系統及便攜式可靈活組網的廣域測量系統[5]的應用，也為線路參數的在線測量提供了條件。目前，相關研究工作主要集中在基于線路雙端同步信息的參數測量[6-10]，而對含有T 接的線路，因T接點的電壓及電流不能直接測量，未有有效算法可進行測量。本文基于不同負荷時段的同步測量信息，對T 接線的線路正序參數進行在線測量，推導了相應理論算法。并且推導了一種分析精度較高的加窗插值傅里葉算法，將其應用于同步采樣數據的分析，克服了在電網頻率發生波動時由于固定采樣頻率導致的頻譜泄漏問題[11-15]，提高了線路參數在線測量的準確度。

2 T 接線路參數在線測量理論算法

關于線路的等效電路，當長度較長（＞300km）時，一般采用均勻分布參數電路，而對于中等長度線路（100～300km）和短線路（＜100km），一般采用集中參數電路[16]。有T 接的線路其各段線路長度一般不會太長，因此采用集中參數電路，分中等長度線路和短線路兩種情況進行線路參數測量算法的推導。

2.1 中等長度線路

對于中等長度線路，各段線路模型采用π形等效電路。T 接線路模型等效電路如圖1 所示。

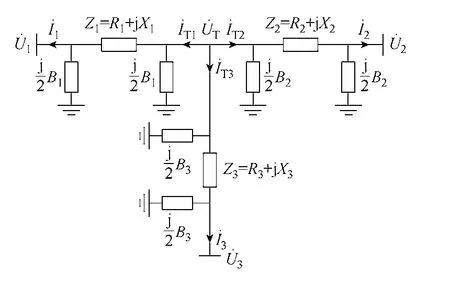
圖1 T接線路等效電路Fig.1 Equivalent circuit of T-connection transmission line

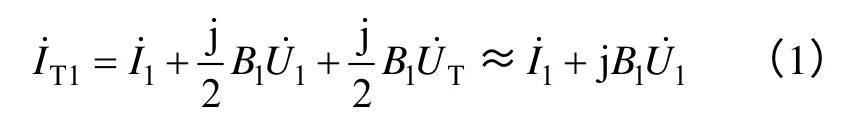
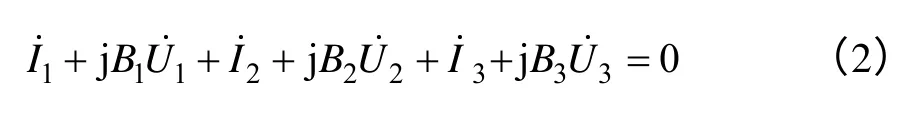
由其他2 時段同步數據可得類同方程，由此可得如下方程組（3 個潮流時段的選擇需保證方程滿秩）：

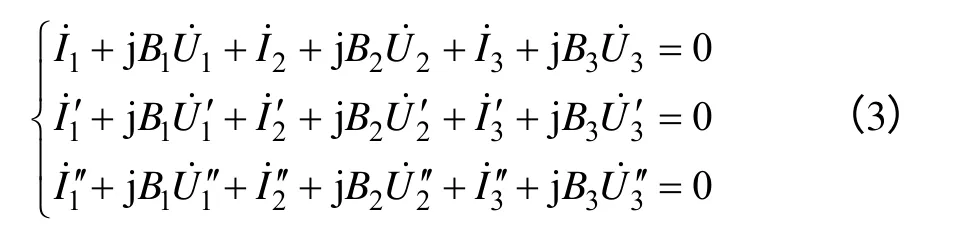
因式（1）做了近似處理，因此，解方程組（3）可得B1、B2和B3的初次近似解，記為：和。

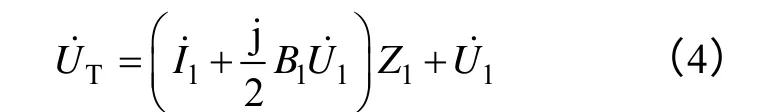
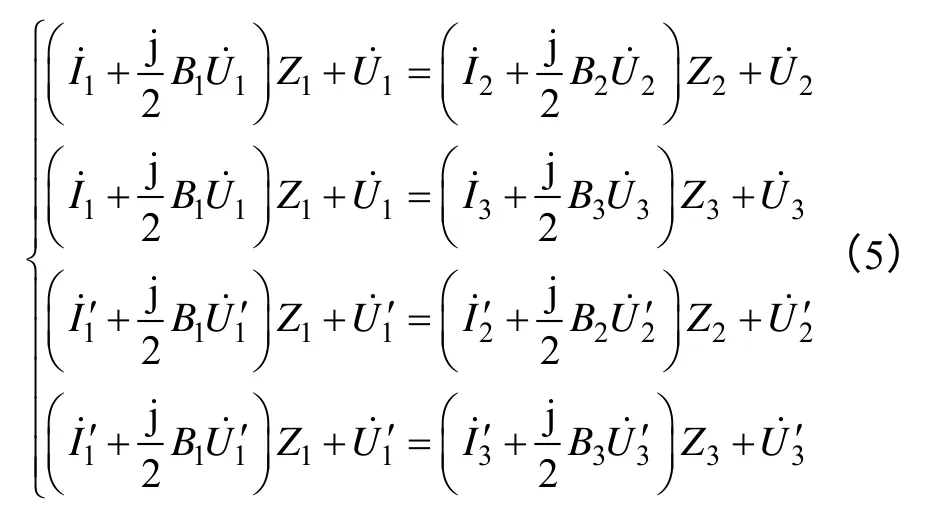
由式（1）得式（3）的準確表達式為

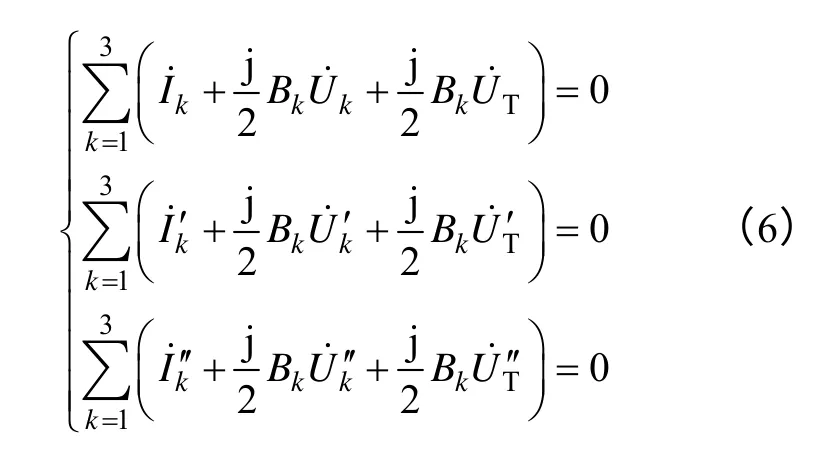
將求得的各支路參數初次解代入式（4）得

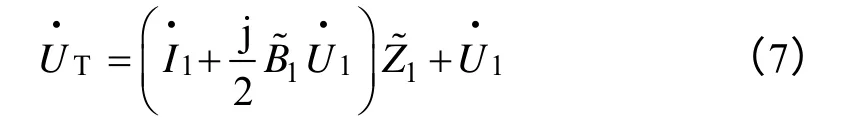
利用測得的同步信息，通過以上兩次迭代求解，得到的T 形接線各個參數值具有較高的準確度。

2.2 短線路

對于短線路，一般可忽略線路的電納B，式（5）變為

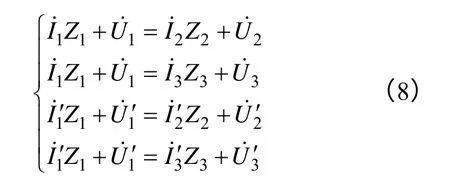
求解式（8）線性方程組即可得各段線路的Z參數。

經仿真驗證，當測量數據準確時，經過二次迭代得到的線路參數具有很高的準確度。實際中，電網頻率總是在一定范圍內波動。PMU 為了保證異地采樣的同步性一般按某一固定頻率采樣，從而在利用FFT 分析數據時易造成數據的非整周期截斷，進而產生頻譜泄漏和柵欄效應，對最終參數測量結果帶來較大誤差。為了解決該問題，本文推導了一種加窗插值FFT 算法。

3 基于加窗插值FFT的采樣數據分析

利用加窗插值FFT 算法可以較好地解決由于數據的非整周期截斷產生的頻譜泄漏現象。為降低頻譜泄漏對信號分析帶來的誤差，應選擇旁瓣峰值電平小且旁瓣漸近衰減速率大的窗函數對信號進行處理。本文選擇的4 項5 階Nuttall[17]窗其時域表示為

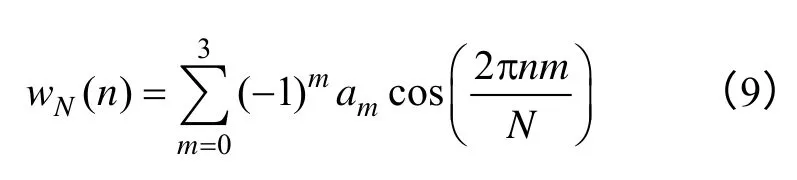
式中，a0=10/32，a1=15/32，a2=6/32，a3=1/32；n=0，1，…，N-1。

該窗函數的旁瓣峰值為-60.95 dB，旁瓣漸近衰減速率為42dB/oct，該窗在保證較大的旁瓣衰減速率的同時，有較小的旁瓣峰值，適合用于信號分析。

以單一頻率信號為例進行分析，設x(t)以采樣頻率fs均勻采樣得到的離散時域信號為

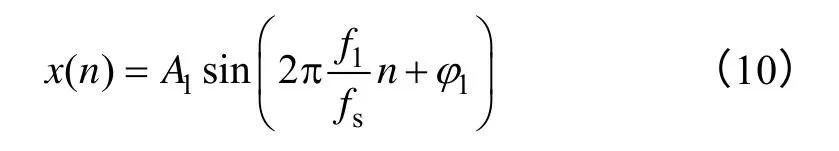
式中，A1、f1、φ1分別為信號的幅值、頻率和初相位，n=0，1，…，N-1，N為采樣點數。

對x(n)加4 項5 階Nuttall 窗得到

加窗序列xw(n)的離散傅里葉變換為

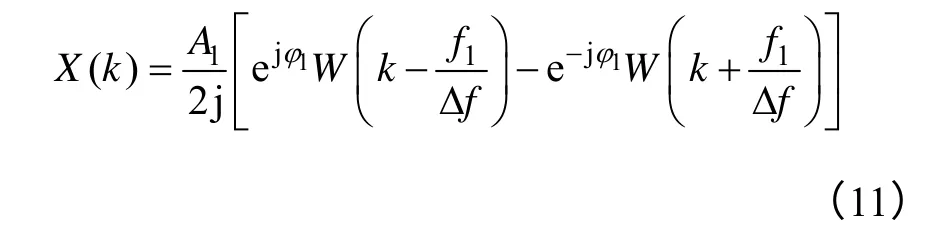
式中，k=0，1，…，N-1，Δf=fs/N，忽略負頻點處頻峰的旁瓣影響，得到加窗信號的離散傅里葉變換表達式為

式中，W(k)為窗函數的離散傅里葉變換，表達式為

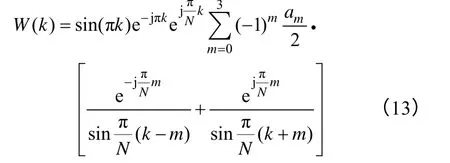
考慮到N?1，式（13）可近似表示為

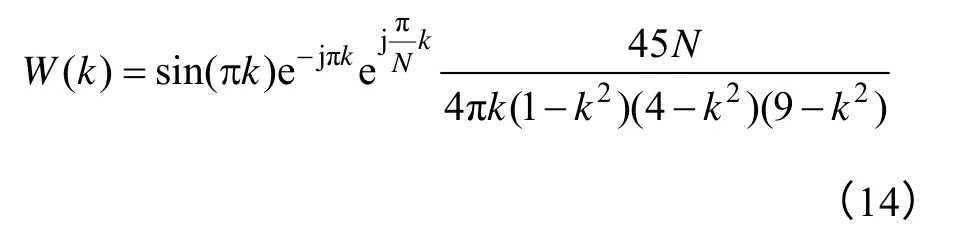
對信號非同步采樣時，信號的頻率kΔf很難正好位于抽樣頻點上，即k一般不是整數。設在峰值頻點附近抽樣得到的幅值最大譜線為ka，其左邊譜線為ka-1，右邊譜線為ka+1，記δ=k-ka，則有-0.5＜δ＜0.5。準確地求得δ是求解問題的關鍵，而δ的大小與ka-1、ka和ka+1三條譜線的幅值|X(ka-1)|、|X(ka)|和|X(ka+1)|密切相關，記

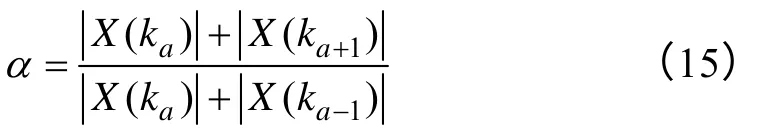
由式（12）和式（14）可得

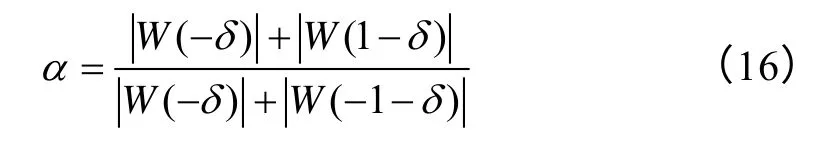
由式（14）和式（16）可得α=(δ+4)/(4-δ)，經變形整理可得

通過式（15）和式（17）求得δ后，可求得信號頻率

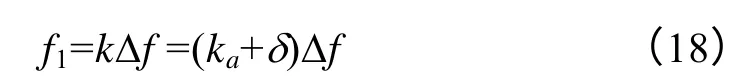
信號的幅值和相位也可通過關于δ的修正函數求得，由式（12）和式（14）可得

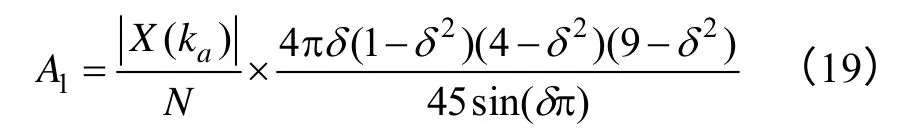
相位的修正公式可表示為

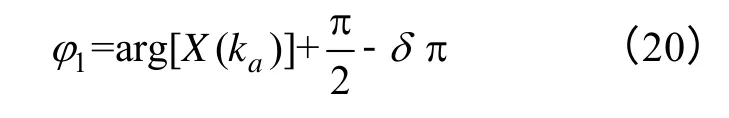
為了驗證以上插值FFT 算法的有效性，采用文獻[15]給出的信號模型進行仿真實驗，該信號無噪聲離散信號的表達式為

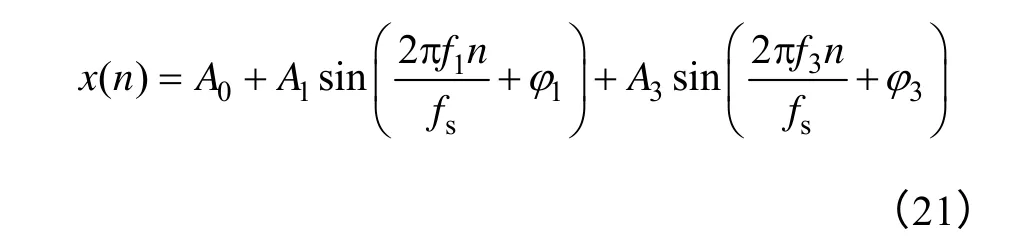
式中，n=0，1，…，N-1，各參數取值為：A0=0.2，A1=6，f1=20.2，φ1=0.1，A3=1，f3=60.6，φ3=0。

式（21）已被眾多文獻用來驗證算法的有效性。本文取：fs=1 000Hz，N=256。在Matlab 環境下仿真，本文算法與加矩形窗[14]、Hanning 窗[14]、Blackman-harris 窗[15]雙譜線插值FFT 進行對比，各算法計算結果的絕對誤差見表1。表1 仿真結果表明，本文算法相對于經典加窗插值FFT 算法有更高的分析精度，用于線路參數的在線測量可獲得更好的效果。

4 仿真驗證

4.1 電網頻率變動對算法的影響

在Matlab 環境下搭建如圖1 所示的含T 形接線的三相電路模型，在節點1 加電源，在節點2 和節點3 加負荷，電壓等級取為110kV，測量數據和線路參數取標幺值，UB=110kV，SB=100MVA，各支路參數取值見表2。

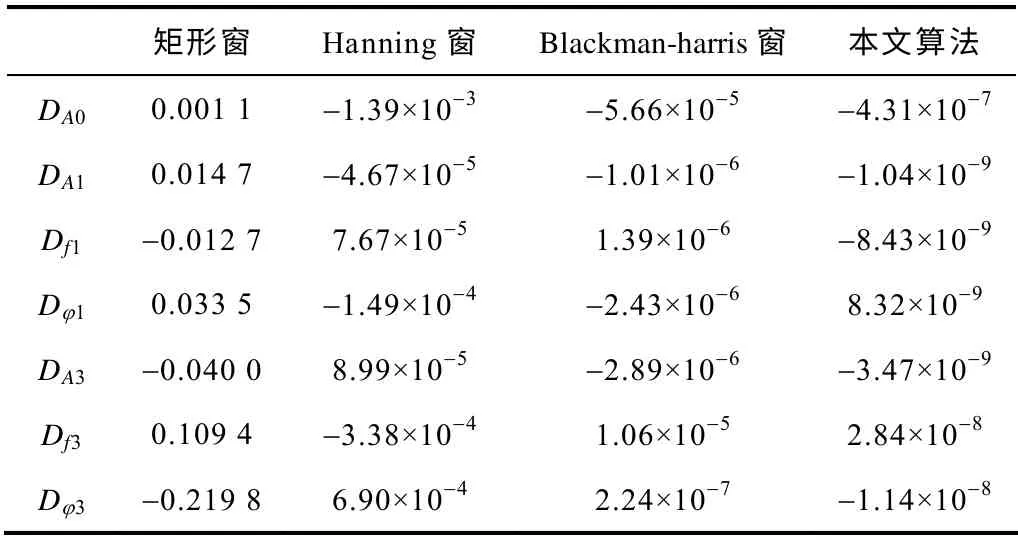
表1 不同加窗插值FFT 算法結果的誤差比較Tab.1 Comparison of simulation results using different window interpolation FFT algorithms

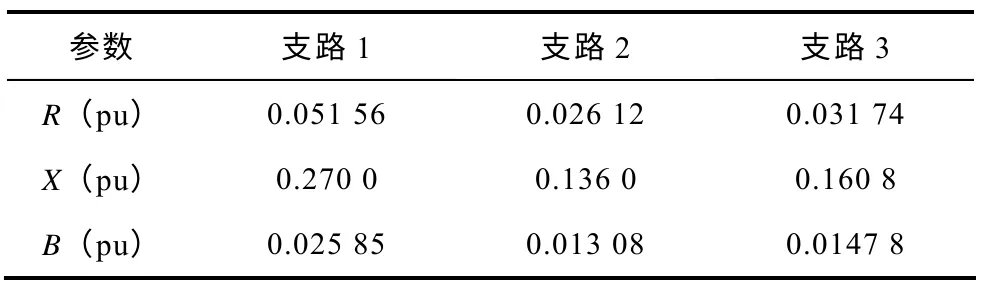
表2 仿真電路中各參數的真值Tab.2 Truth-values of the artificial circuit parameter

通過改變節點2 和節點3 負荷的大小，得到3種不同潮流時段的離散同步采樣數據。對信號的采樣頻率取10kHz，數據長度取2 000 點，對采樣數據利用第3 節所述加窗插值FFT 算法進行分析，得到三相基波電壓、電流相量，用對稱分量法求得正序分量，按第2 節方法計算T 接線路參數。電網頻率在49.50～50.50Hz 變動時各參數測量結果的相對誤差見表3。

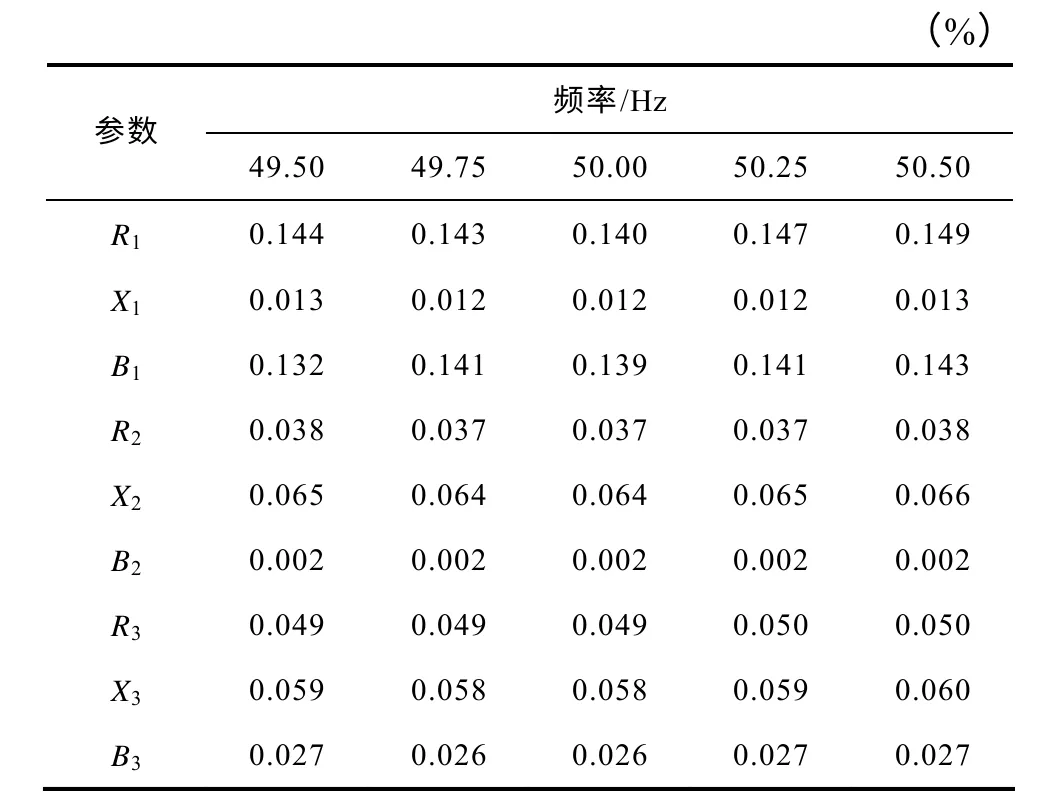
表3 不同電網頻率下測量結果的相對誤差Tab.3 Relative error of measurement under different frequency

從表3 數據可以看出，當電網頻率在49.5～50.5Hz 變動時，線路參數測量都具有較高的準確度，電阻的測量誤差相對較大，但其最大誤差也小于0.15%。

4.2 白噪聲對算法的影響

在實際測量中，測得的數據都是含有白噪聲的。為了驗證算法在采樣數據含有白噪聲情況下的有效性，進行了仿真，模型同前，電網頻率取50.50Hz，對測量的三相電壓和電流離散采樣信號加入高斯白噪聲，不同信噪比下線路參數測量結果相對誤差以第1 段線路為例列出，結果見表4。

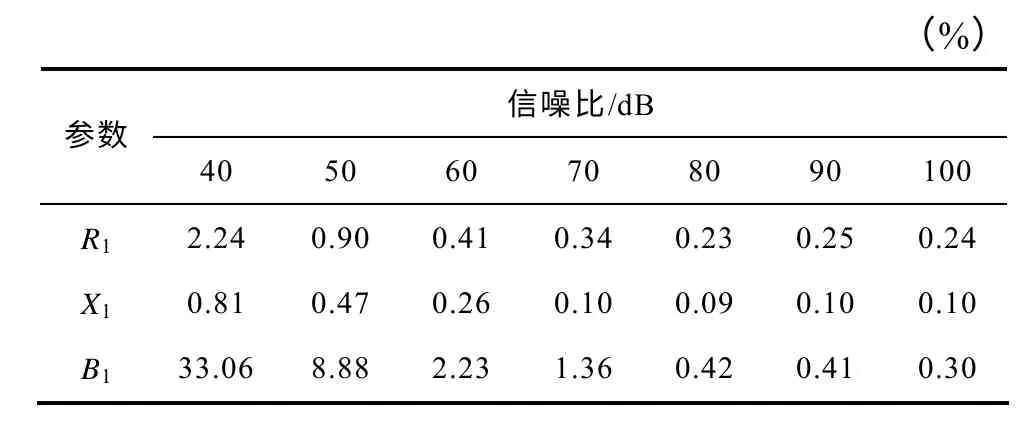
表4 不同信噪比下測量結果的相對誤差Tab.4 Relative error of measurement under different SNR

由表4 數據可以看出，信噪比較低（＜50dB）時，各參數測量誤差均較大。當信噪比大于60dB時，R和X的測量誤差均小于0.5%，而B的測量準確度受信噪比影響較大，但在信噪比大于60dB 時其誤差小于5%。

5 現場實際運行

利用研制的廣域測量系統對河北南網一處含T接線路進行了在線測量，線路示意圖如圖2 所示，支路1 為220 kV 變電站的一條出線，支路2 和支路3 分別為2 座110 kV 變電站的進線，各段線路型號及長度標于圖3 中。線路參數的設計值見表5。

圖2 被測的T 接線示意圖Fig.2 Schematic diagram of the measured T-connection line

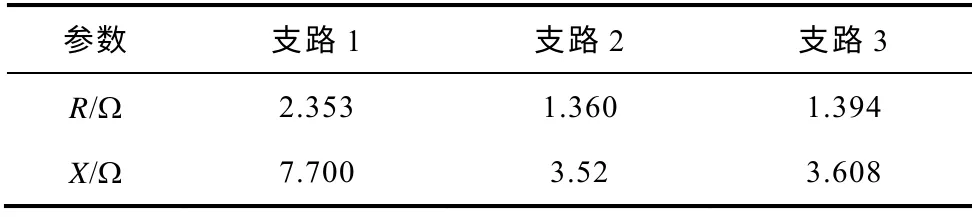
表5 T 接線參數設計值Tab.5 Design values of the T-connection line parameters

便攜式PMU 安裝于3 個變電站，進行了一段時間的同步測量。PMU 每隔5min 進行一次同步采樣，并將數據通過GPRS 無線網絡傳送至數據處理中心。監測完成后由數據處理中心自動篩選負荷差異較大時段的同步采樣數據，進行線路參數的計算，因線路長度較短，忽略B參數，若干次測量結果及其平均值見表6。

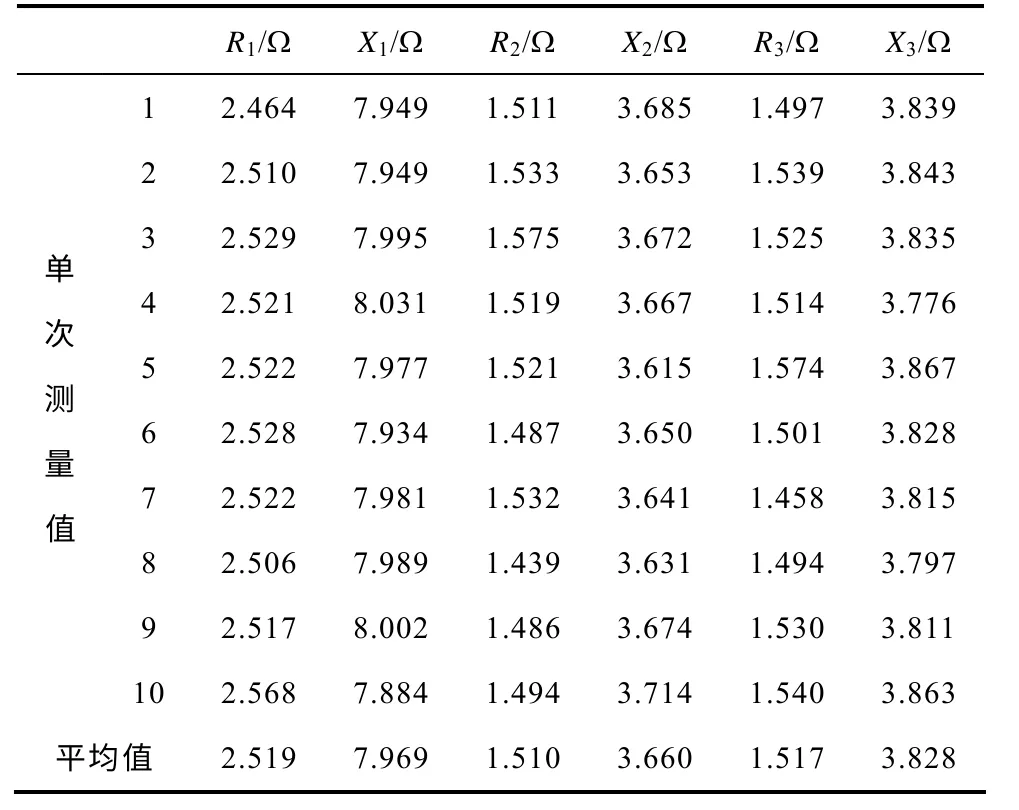
表6 T 接線參數實測結果Tab.6 Measurement results of the T-connection line parameters

通過實際測量發現，單次測量值在一定范圍內波動，尤其是電阻值較小的R2和R3波動相對較大，通過求平均值可獲得相對較為穩定的測量結果，因此，取其平均值作為最終測量值。

通過對比在線測量值和設計值發現，兩者存在一定差別，電阻相差約在6%～10%，電抗相差約在2%～5%。分析其原因，在于兩個方面：①隨著線路的運行老化及環境的變化，設計值偏離其真實值；②由于系統PT、CT的誤差及PMU的測量誤差，導致在線測量值與真實值之間存在差別。

為了比較參數在線測量值和設計值哪個更接近真實值，利用SCADA 系統提供的數據進行驗證，由SCADA 系統獲取的與T 接線3 端相關的視在功率S（注入母線為正）和線電壓U的一組數據見表7。

表7 T 接線相關的SCADA 數據Tab.7 Data of T-connection line obtained from SCADA

根據節點2 和節點3的SCADA 數據分別利用線路的設計參數和實測參數計算節點1的U和S，與SCADA 系統提供的節點1的U和S對比。利用線路設計參數計算得到的節點1的線電壓、有功和無功量與 SCADA 提供的對應值之差為：ΔU1=0.35kV，ΔP1=346kW，ΔQ1=203kvar；利用線路實測參數計算得到的節點1的線電壓、有功和無功量與SCADA 提供的對應值之差為：ΔU1=0.21kV，ΔP1=318kW，ΔQ1=159kVar。由此可見，線路參數取在線測量值時，3 個變電站SCADA 數據的吻合度比線路參數取設計值要好，驗證了在線測量值的準確可靠。

6 結論

本文提出的利用含T 接輸電線路三端多時段同步測量信息進參數在線測量的方法，經過了河北南網110 kV 含T 接線路正序參數帶電測量的檢驗，證明方法是正確可行的，測量結果能夠滿足工程要求。

本文所提方法對三繞組變壓器及其他電力系統元件參數的在線測量也有一定借鑒意義。

[1]陳允平,張承學,胡志堅.以 GPS 為基礎的線路參數帶電測量[J].電力系統自動化,1998,22(6):43-45.Chen Yunping,Zhang Chengxue,Hu Zhijian.Zero-sequence parameter measurement under operation of transmission line with mutual inductance based on GPS technology[J].Automation of Electric Power Systems,1998,22(6):43-45.

[2]Borda C,Olarte A,Diaz H.PMU-based line and transformer parameter estimation[C].2009 IEEE Power Systems Conference and Exposition(PSCE2009),Seattle,Washington,USA,2009:1-8.

[3]王茂海,鮑捷,齊霞,等.基于PMU 實測數據的輸電線路參數在線估計方法[J].電力系統自動化,2010,34(1):25-27,31.Wang Maohai,Bao Jie,Qi Xia,et al.Online estimation of transmission line parameters based on PMU measurements[J].Automation of Electric Power Systems,2010,34(1):25-27,31.

[4]于淼.基于同步相量測量技術的線路參數在線辨識[D].天津:天津大學,2005.

[5]Liang Zhirui,Niu Shengsuo,Su Haifeng,et al.Research of flexible wide-area measurement and analysis system in power system[C].2010 International Conference on Electricity Distribution(CICED 2010),Nanjing,China,2010:1-4.

[6]柴京慧,李書敏,何樺.基于PMU 及多時間斷面的輸電網參數估計[J].電力系統自動化,2009,33(11):49-52.Chai Jinghui,Li Shumin,He Hua.Parameter estimation based on PMU and multi-cases of SCADA for electricity transmission network[J].Automation of Electric Power Systems,2009,33(11):49-52.

[7]李欽,項鳳雛,顏偉,等.基于SCADA 及PMU 多時段量測信息的獨立線路參數估計方法[J].電網技術,2011,35(2):105-109.Li Qin,Xiang Fengchu,Yan Wei,et al.An approach to estimate parameters of single transmission line based on multi-interval information measured by SCADA and phasor measurement units[J].Power System Technology,2011,35(2):105-109.

[8]李澍森,陳曉燕,吳彥皎,等.多回平行輸電線路參數帶電測量[J].電力系統自動化,2009,33(22):84-87,97.Li Shusen,Chen Xiaoyan,Wu Yanjiao,et al.Live line measurement of several parallel transmission lines[J].Automation of Electric Power Systems,2009,33(22):84-87,97.

[9]胡志堅,陳允平,徐瑋,等.基于微分方程的互感線路參數帶電測量研究與實現[J].中國電機工程學報,2005,25(2):28-33.Hu Zhijian,Chen Yunping,Xu Wei,et al.Principles and realization of live line measurement of parameters of transmission lines with mutual inductance based on differential equations[J].Proceedings of the CSEE,2005,25(2):28-33.

[10]Yuan Liao,Kezunovic.Online optimal transmission line parameter estimation for relaying applications[J].IEEE Transactions on Power Delivery,2009,24(1):96-102.

[11]Andria G,Savino M,Trotta A.Windows and interpolation algorithms to improve electric measurement accuracy[J].IEEE Transactions on Instrumentation and Measurement,1989,38(8):856-863.

[12]Jain Vijay K,Collins Willim L.High-accuracy analog measurements via interpolated FFT[J].IEEE Transactions on Instrumentation and Measurement,1979,28(2):113-122.

[13]潘文,錢俞壽,周鶚.基于加窗插值FFT的電力諧波測量理論(Ⅱ)—雙插值FFT 理論[J].電工技術學報,1994,9(2):53-56.Pan Wen,Qian Yushou,Zhou E.Power harmonies measurement based on windows and interpolated FFT(Ⅱ)—dual interpolated FFT algorithms[J].Transactions of China Electrotechnical Society,1994,9(2):53-56.

[14]龐浩,李東霞,俎云霄,等.應用 FFT 進行電力系統諧波分析的改進算法[J].中國電機工程學報,2003,23(6):49-54.Pang Hao,Li Dongxia,Zu Yunxiao,et al.An improved algorithm for harmonic analysis of power system using FFT technique[J].Proceedings of the CSEE,2003,23(6):49-54.

[15]許珉,張鴻博.基于Blackman-harris 窗的加窗FFT 插值修正算法[J].鄭州大學學報(工學版),2005,26(4):99-101.Xu Min,Zhang Hongbo.The correction algorithm based on the Blackman-harris windows and interpolated FFT[J].Journal of Zhengzhou University(Engineering Science),2005,26(4):99-101.

[16]陳珩.電力系統穩態分析[M].北京:中國電力出版社,2007.

[17]Nuttall A H.Some windows with a very good sidelobe behavior[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1981,29(1):84-91.