具有多參數(shù)的奇攝動(dòng)非線(xiàn)性邊值問(wèn)題的攝動(dòng)解
李超,王曉云
(1.中北大學(xué)理學(xué)院,山西太原 030051;2.山西警官高等專(zhuān)科學(xué)校基礎(chǔ)部,山西太原 030021)
具有多參數(shù)的奇攝動(dòng)非線(xiàn)性邊值問(wèn)題的攝動(dòng)解
李超1,王曉云2
(1.中北大學(xué)理學(xué)院,山西太原 030051;2.山西警官高等專(zhuān)科學(xué)校基礎(chǔ)部,山西太原 030021)
討論含多個(gè)參數(shù)的高階非線(xiàn)性方程的攝動(dòng)解,在適當(dāng)?shù)臈l件下,先構(gòu)造出外部解,再根據(jù)不同的邊界層,利用伸展變量和冪級(jí)數(shù)展開(kāi)式理論,構(gòu)造問(wèn)題的形式漸近解,最后利用微分不等式理論證明漸近解的一致有效性和漸近形態(tài),把奇攝動(dòng)非線(xiàn)性問(wèn)題中的參數(shù)推廣到多個(gè)參數(shù).
非線(xiàn)性;多參數(shù);奇攝動(dòng);邊值問(wèn)題;邊界層校正
1 引言
對(duì)于含小參數(shù)非線(xiàn)性系統(tǒng)(奇攝動(dòng)非線(xiàn)性系統(tǒng))邊界層研究一直是眾多致力于非線(xiàn)性系統(tǒng)工作者非常關(guān)注的問(wèn)題[1-6].近幾十年來(lái),處理奇攝動(dòng)非線(xiàn)性系統(tǒng)邊界層的很多方法已經(jīng)陸續(xù)被提出,并不斷被優(yōu)化.其中一些經(jīng)典的方法有邊界層法、匹配漸近展開(kāi)法、多重尺度法等.另外,一些學(xué)者還利用微分不等式方法來(lái)研究奇攝動(dòng)非線(xiàn)性系統(tǒng),如文獻(xiàn)[7-15]利用微分不定式等方法研究了奇攝動(dòng)非線(xiàn)性常微分方程邊值問(wèn)題、反應(yīng)擴(kuò)散方程、橢圓型方程邊值問(wèn)題、奇攝動(dòng)問(wèn)題的激波層解和大氣物理問(wèn)題等.文獻(xiàn)[16]利用微分不等式研究了兩個(gè)參數(shù)的非線(xiàn)性方程的奇攝動(dòng)解.本文在文獻(xiàn)[16]的基礎(chǔ)上,討論了一類(lèi)具有n個(gè)參數(shù)的非線(xiàn)性奇攝動(dòng)邊值問(wèn)題,并證明了解的一致有效性.
考慮如下非線(xiàn)性奇攝動(dòng)邊值問(wèn)題:
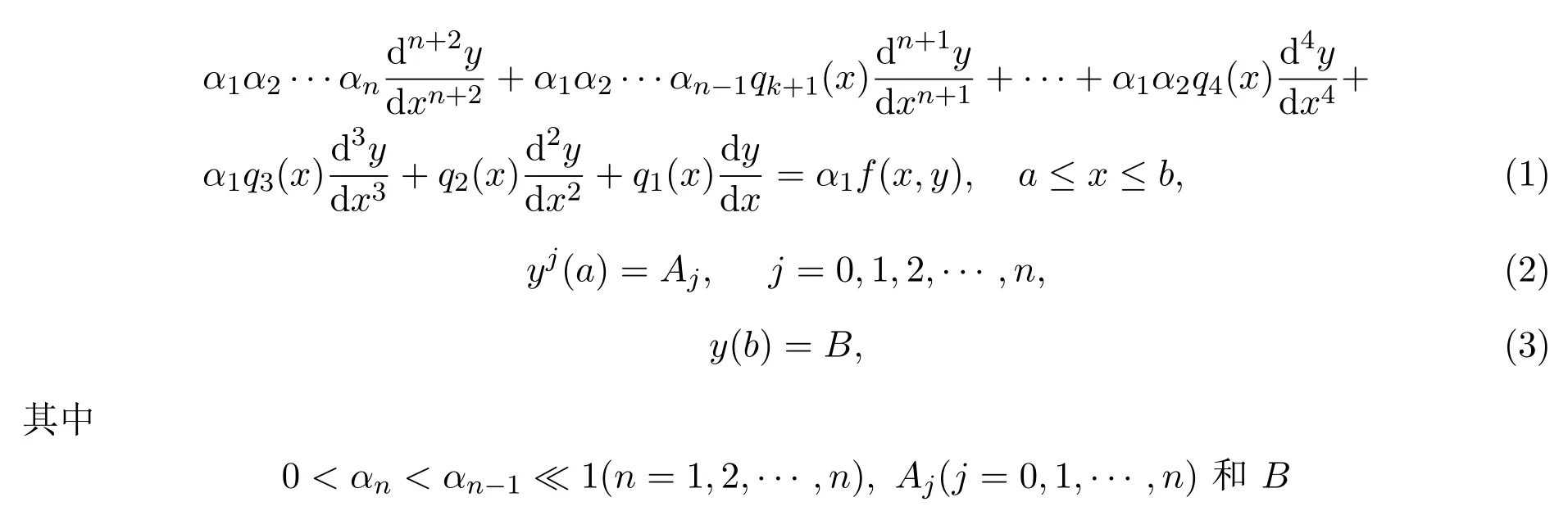
為常數(shù).為了方便,此處把(1)-(3)式記為系統(tǒng)(N).

2 方程的形式漸近解
2.1 外部解

依次可求得

顯然,由(9)式得到的解Y0就是退化問(wèn)題(4)-(5)的解Y0(x),且由(10)式可以依次地得到Y(jié)i,這樣就得到外部解

但是它并不滿(mǎn)足j=1,2,…,n時(shí)的邊界條件,所以需要構(gòu)造在x=a附近的第一,第二,…,第n邊界層校正項(xiàng).
2.2 第一邊界層校正
為了得到系統(tǒng)(N)形式漸近解的一致有效展開(kāi)式,下面在不同的邊界層引入伸長(zhǎng)不同的變量來(lái)構(gòu)造函數(shù).
定義1.1中間方程:方程(1)某一系數(shù)趨于零時(shí)得到的方程稱(chēng)為中間方程.
現(xiàn)考慮(6)式的中間方程


2.3 第二邊界層校正


2.4 第n邊界層校正


3 解的一致有效性證明


[1]De Jager EduardusMarie,Jiang Furu.The Theory of Singular Perturbation[M].Am sterdam:North-Holland Publishing Co.,1996.
[2]NiWeim ing,Wei Juncheng.On positive solution concentrating on spheres for the Gierer-Meinhard t system[J].Journal of Differential Equations,2006,221(1):158-189.
[3]Zhang Fu.Coexistence of a pulse and mu ltip le spikes and transition layers in the standing waves of a reation-diffusion system[J].Journal of D ifferential Equations,2004,205(1):77-155.
[4]Khasm inskii Refail Zalmannovich,Yin George.Lim it behavior of two-time-scale diffusion revisited[J]. Journal of D ifferential Equations,2005,212(1):85-113.
[5]Marques Iim a.Existence and asym p totic behavior of solutions for a class of nonlinear ellip tic equationswith Neum ann condition[J].Non linear Analysis,2005,61(1):21-40.
[6]Bobkova A S.The behavior of solutionsmu ltidim ensional singu larly perturbed system with one fast variable[J].Journal of Differential Equations,2005,41(1):23-32.
[7]Mo Jiaqi.A singularly perturbed non linear boundary value p roblem[J].Journal of Mathem atical Analysis and App lications,1993,178(1):289-293.
[8]Mo Jiaqi.Singular perturbation for a class of nonlinear reaction diffusion system[J].Science in China:Ser. A,1989,32(11):1306-1315.
[9]莫嘉琪,朱江.非線(xiàn)性非局部反應(yīng)擴(kuò)散方程奇攝動(dòng)問(wèn)題[J].應(yīng)用數(shù)學(xué)和力學(xué),2003,24(5):446-470.
[10]莫嘉琪,王輝,林萬(wàn)濤.一類(lèi)具有邊界攝動(dòng)的非線(xiàn)性非局部反應(yīng)擴(kuò)散方程奇攝動(dòng)問(wèn)題[J].應(yīng)用數(shù)學(xué)和力學(xué), 2005,26(12):1507-1510.
[11]Mo Jiaqi.The singu larly perturbed boundary value problem s for higher-order sem ilinear elliptic equation[J]. Advances in Mathem atics,2001,30(2):141-148.
[12]莫嘉琪,王輝.一類(lèi)非線(xiàn)性激波問(wèn)題位置的轉(zhuǎn)移[J].應(yīng)用數(shù)學(xué)和力學(xué),2005,26(1):53-57.
[13]Mo Jiaqi,Lin Wantao,Zhu Jiang.A variational iteration solvingmethod for ENSO mecham ism[J].Progress in Natural Science,2004,14(12):1126-1128.
[14]Mo Jiaqi,Wang Hui,Lin Wantao,et al.Sea-air oscillator model for Pacific SST[J].Acta Phys Sinica, 2006,55(1):6-9.
[15]Mo Jiaqi,Wang Hui,Lin Wantao,et al.Varitional iterationmethod themechanism of the equatorialeastern Pacific EINino-Southern oscillator[J].Chinese Physics,2006,55(4):671-675.
[16]陳麗華,莫嘉琪.具有雙參數(shù)的非線(xiàn)性方程的奇攝動(dòng)解[J].應(yīng)用數(shù)學(xué)和力學(xué),2007,28(10):1197-1202.
[17]O′Malley Robert Emm ett.introduction to Singu lar[M].New York:Academ ic Press,1974.
Singu larly perturbed solution for nonlinear equations with some parameters
Li Chao1,Wang Xiaoyun1,2
(1.College of Science,North University of China,Taiyuan 030051,China; 2.Departm ent of Mathem atics,Shanxi Police Academ y,Taiyuan 030021,China)
A class of nonlinear speed system perturbed solution non local prob lem is discussed in this paper.In approp riate conditions,first constructed out external solution,again according to different boundary layer and using stretchy variable and power series launched theory,the asym ptotic expansions of solution of this p roblem is shown and p roved to be uniform ly effective using the theory of differential inequality in the whole interval. This paper extends the perturbed problem of the parameters of the parameters of the p romotion to multip le param eters.
nonlinear,m any param eters,singularly perturbed,boundary value prob lem, boundary layer correction
O178
A
1008-5513(2012)03-0370-08
2012-01-23.
山西省自然科學(xué)基金(2011011002-1);中國(guó)博士后科學(xué)基金(20100471857).
李超(1987-),碩士生,研究方向:應(yīng)用數(shù)學(xué).
2010 MSC:15A 42

