基于FPGA的無人機MLS中頻接收機研究與實現
王 偉, 張 斌, 吳 松
(空軍工程大學電訊工程學院,西安 710077)
0 引言
大型無人機自主著陸問題是影響無人機飛行安全和出勤率的重要因素。國外無人機自主著陸多采用基于GPS的組合導航方式。國內無人機自動起降系統功能和性能還不能完全滿足要求,相關標準尚未確立。微波著陸系統(MLS)是目前國內機場配備的精度最高的飛機進近著陸系統,其特點是信號覆蓋空間大,精度高,受場地環境影響小,所提供的進近方式更加靈活[1]。采用MLS作為無人機的自主導航系統,可以充分利用現有地面資源,在飛機上安裝一部接收機,提供精密的制導信息,同時擺脫了GPS受制于人的缺陷。因此,研究MLS信號的高精度解調具有十分重要的意義。
MLS信號中的數字信息采用2DPSK調制方式,采用相干解調精度較高,對MLS信號進行相干接收時,要求本地載波與接收信號載波同頻同相,載波同步的方法包括直接法和插入導頻法,其中插入導頻法要求輸入信號含有載頻信息,此處并不適用。直接法包括Costas環和平方環[2],平方環法需要倍頻,頻率較高時在工程上難以實現。Costas環是一種閉環自適應系統,能夠高速高精度地完成載波同步和2DPSK解調,傳統的模擬Costas環因存在同相支路與正交支路的不平衡性從而使環路的性能受到一定的影響,且模擬電路還存在直流零點漂移、難以調試等缺點,采用全數字的實現方式則可有效地避免這些問題[3]。另外,采用數字解調方式還具有體積小、重量輕、功耗低,調試簡單等優點。
MLS的測角是基于時基掃描波束技術,通過測量“往返”掃描脈沖的時間間隔完成測角功能,因此,需要對MLS信號進行AM解調,得到掃描脈沖的包絡,AM解調的精度直接影響著測角的精度。應用CORDIC算法設計Costas環的鑒相器和AM解調關鍵模塊,這樣,利用Costas環的部分電路就可以實現高精度數字正交AM解調。
1 MLS信號格式
MLS信號格式采用時分多路復用體制,方位制導、仰角制導和數據字信號工作在同一頻率,各自占有一定的發射時隙[4]。方位和仰角信號的基本格式是前導碼加扇區信號加掃描信號,數據字信號的基本格式是前導碼加數字信息。前導碼信號、扇區信號和數字信息為2DPSK調制信號,調制速率為15625 Hz,掃描信號為AM信號。前導碼包括3部分:載波捕獲段、基準時間碼和功能識別碼。載波捕獲段為832 μs的未加調制載波,在此期間完成載波同步;基準時間碼為5位巴克碼,作用是產生時間基準;功能識別碼的作用是區分接收信號的功能(發射的是方位信號、仰角信號還是數據字)。
2 MLS信號載波同步及AM解調原理
MLS信號工作在C波段(5031~5091 MHz),經天線接收后無法直接進行處理,在射頻電路中經過兩次下變頻得到65 MHz中頻信號,然后進行數字帶通采樣,根據帶通采樣定理,采樣速率確定為8 MHz,采樣后將中心頻率為1 MHz的信號濾出,其攜帶有MLS信號的完整信息。
傳統的Costas環只有一路反饋,同時調整本地頻率和相位,捕獲帶較窄,相位抖動幅度大,對環路進行改進,增加鑒頻電路,設計兩路反饋,分別調整本地頻率和相位,捕獲帶較寬,相位抖動幅度小。
AM解調基于數字正交解調原理,具有較強的抗載頻失配能力,即允許本地載波與信號載波之間有一定的頻差和相差。Costas環及AM解調的綜合實現框圖如圖1所示。
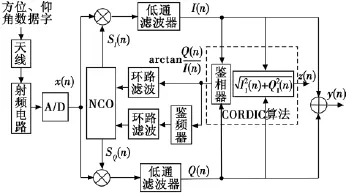
圖1 Costas環實現載波同步及AM解調原理Fig.1 Principle of carrier synchronizer based on Costas and AM demodulation
設經過A/D采樣后,得到的2DPSK調制信號和AM信號分別為
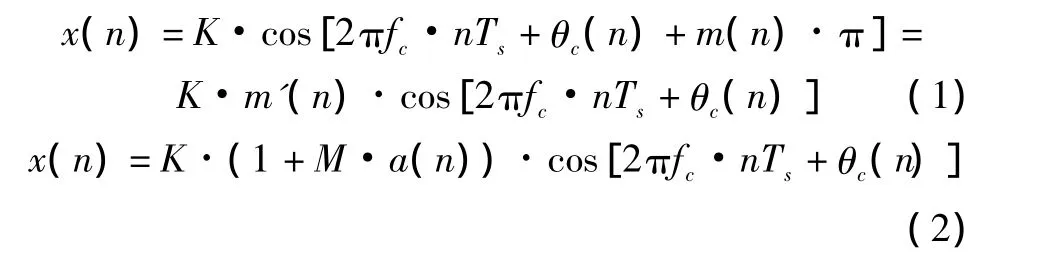
其中:m(n)為攜帶的數字基帶信息,當m(n)=0時,m'(n)=1,當m(n)=1時,m'(n)=-1;K為輸入信號的幅值;fc為經過A/D后的載頻;θc(n)為瞬時相位;Ts為信號采樣周期;1+M·a(n)為信號包絡。
NCO輸出兩路正交信號為
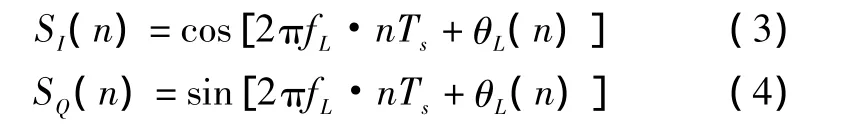
其中:fL為本地載頻;Ts為采樣周期;θL(n)為本地瞬時相位。
2DPSK調制信號經過數字混頻和低通濾波器濾除高頻分量后得到
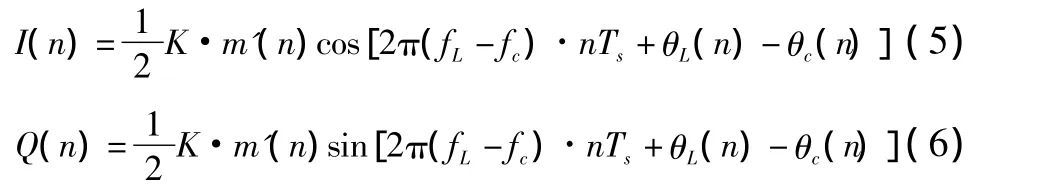
在鑒相器中,根據式(5)和式(6)求反正切得到瞬時相位差2π(fL-fc)·nTs+θL(n)-θc(n),對相位差求一階導數可以得到瞬時頻率增量2π(fL-fc)·Ts,瞬時頻率增量經過鑒頻環路濾波器后調整NCO的頻率,在完成頻率鎖定即瞬時頻率增量為0后,瞬時相位增量經過鑒相環路濾波器后調整NCO的相位,完成相位鎖定即瞬時相位差為0,此時將同相分量I(n)和正交分量Q(n)相加后可得到輸出信號為
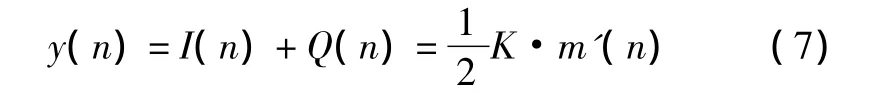
對y(n)進行相對碼到絕對碼的轉換就得到數字基帶信息。從整個解調過程可以看出,2DPSK解調實質上是Costas環鎖相過程。因此,只要在832 μs內完成數字鎖相,就可以準確地得到MLS地面設備發出的2DPSK基帶信號。
根據MLS信號格式,實現載波同步后,進行基準時間碼同步,功能碼識別,如為數據字信號,則繼續進行2DPSK解調,如為角度制導信號,則進行AM解調。AM信號經過相同過程得到I(n)和Q(n)。
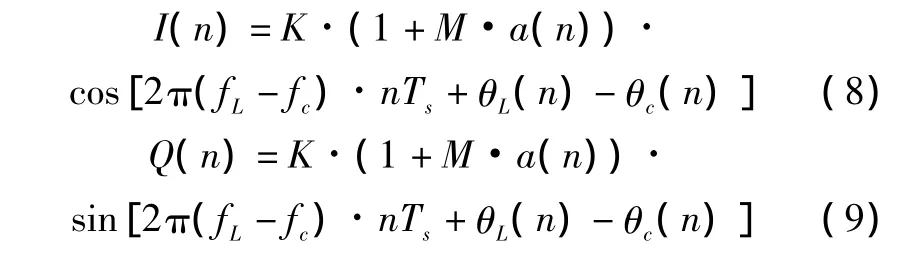
計算I(n)和Q(n)的平方和再開方就得到了信號的包絡。
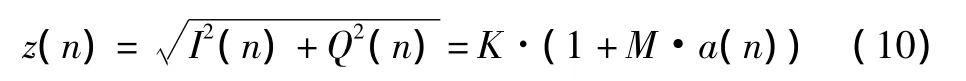
從推導過程可以看出,當接收信號載波與本地載波不同步時,AM解調精度不變。
3CORDIC算法
CORDIC算法可以通過簡單的加法移位操作迭代計算 sin θ,cos θ,arctan θ等函數,避免了使用泰勒級數展開式計算所需的復雜乘法運算,特別適合于FPGA實現[5]。推廣的CORDIC算法適用于圓周坐標、線性坐標和雙曲線坐標,每種坐標系又分為向量模式和旋轉模式,統一迭代方程如下。
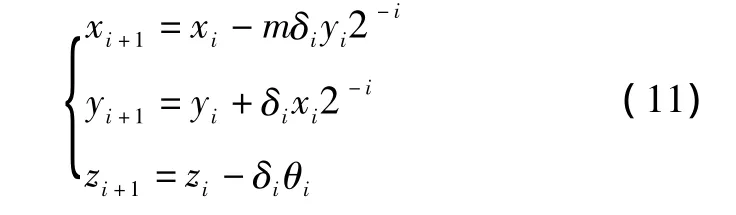
其中
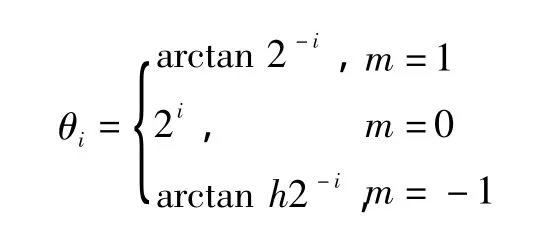
式中:m代表坐標系,δi代表旋轉方向,θi代表旋轉的角度,根據m和δi取值的不同,CORDIC算法可經過不同的設置實現不同的數學運算。
3.1 基于CORDIC算法的NCO設計
NCO的作用是產生正交的正弦和余弦樣本,傳統做法是采用查表法(LUT),即事先根據各個正/余弦波相位計算好相位的正/余弦值,并按相位角度作為地址在存儲器中對其進行尋址,構成一個幅度/相位轉換電路(即波形存儲器),通過該轉換電路進行查表獲得正/余弦信號樣本。為了提高數控振蕩器的頻率分辨率,往往需要擴大波形存儲器的容量,占用大量資源。為了避免這一問題,考慮利用算法實時產生正/余弦樣本,CORDIC算法正好滿足這一需求。
應用CORDIC算法圓周旋轉模式產生正余弦信號[6],令 m=1,則 θi=arctan 2-i,給定初值,x0=K1,y0=0,z0= φ,其中旋轉方向由zi決定,若zi<0,則 δi=+1;若zi>0,則 δi=-1,經過n次迭代最終使zi趨于0。迭代的最終結果為
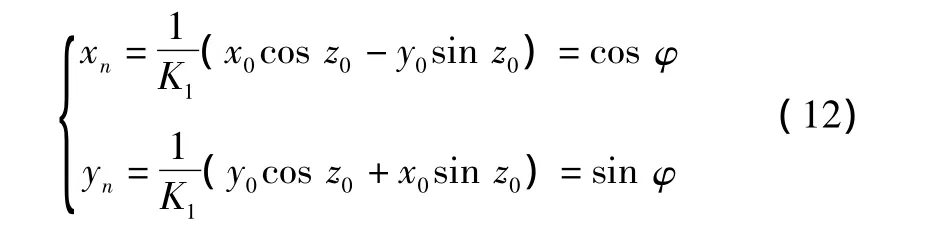
數控振蕩器(NCO)的總體實現框圖如圖2所示,主要由頻率調整累加器、相位累加器、相位加法器和CORDIC算法計算正余弦模塊構成。
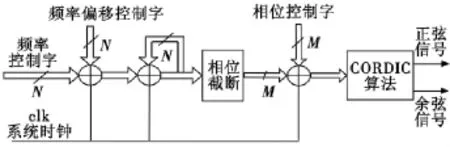
圖2 數控振蕩器(NCO)結構框圖Fig.2 Block diagram of NCO
在系統時鐘的控制下,頻率偏移控制字不斷調整頻率控制字,對N位頻率控制字進行累加,截取輸出值的高M位與相位控制字相加,這樣,每來一個時鐘得到一個相位,用CORDIC算法計算該相位的正余弦值。當同步以后,維持頻率控制字和相位控制字不變,NCO輸出與接收信號同頻同相的載波信號。
3.2 基于CORDIC算法的鑒相鑒頻器和AM解調關鍵模塊設計
數字鑒相器作為載波跟蹤環路的核心部分,其精度和鑒相范圍直接影響接收機的性能,數字鑒相的方法主要有4種:I·Q型、sign(I)·Q型、Q/I型、arctan(Q/I)型,其中基于反正切的相位誤差檢測最為精確,相比其他鑒相方法能夠相對降低環路抖動[7],因此,采用arctan(Q/I)型鑒相器。傳統的實現反正切方法是首先對同相支路(Q路)和(I路)做除法,然后根據反正切查找表找到其對應反正切值,缺點是除法硬件實現困難,查找表占用資源多。利用CORDIC算法可以解決這些問題。
從AM解調原理可以看出,重難點在于計算同相支路和正交支路的平方和再開方,計算平方和可以用兩個乘法器和一個加法器實現,傳統的開平方計算算法主要有實函數近似法、牛頓迭代法、冗余算法等,這些算法從根本上講是使用了查表法或多項式展開近似,它們的速度和精度難以滿足實用要求,硬件實現也非常困難,利用CORDIC算法計算平方和再開方,省去了乘法器和加法器,只有加法和移位,易于工程實現。
應用 CORDIC 算法圓周矢量模式[8],令 m=1,則θi=arctan 2-i,給定初值,x0=I(n),y0=Q(n),z0=0,旋轉方向由 yi決定,若 yi<0,則 δi=+1,若 yi>0,則δi=-1,經過n次迭代最終使yi趨于0。迭代的最終結果為
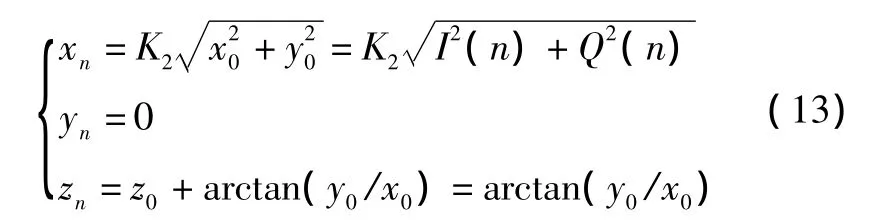
模擬域相位函數和模擬角頻率函數之間關系為
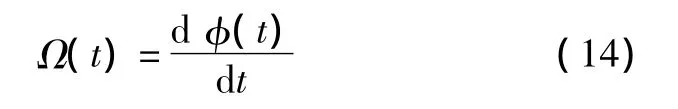
可以得到數字域的相位函數φ(n)和頻率函數f(n)之間的關系為
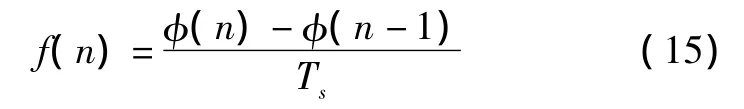
其中,Ts為采樣周期。考慮到數字域的數字頻率ω(n)=f(n)·Ts,所以式(15)可以轉化為
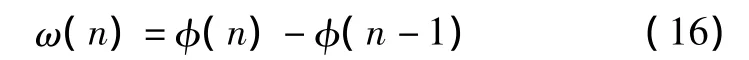
式(16)表明數字域頻率和相位的關系是簡單的一階差分關系,所以只要利用CORDIC算法得到的瞬時相位差進行一階差分就可以得到瞬時頻差。
當檢測到有輸入信號時,鑒頻環路濾波器開始工作,瞬時頻差經過鑒頻環路濾波器后作為頻率偏移控制字不斷調整NCO的頻率控制字,直至完成頻率同步,鑒頻環路濾波器停止工作,鑒相環路濾波器開始工作,瞬時相差經過鑒相環路濾波器作為相位控制字不斷調整NCO的相位,直至完成相位同步。
4 FPGA實現及信號分析
根據以上設計理論,在QuartusII8.0設計平臺上用VHDL語言編程實現。CORDIC算法的實現方式有兩種:基于狀態機結構和基于流水線結構。狀態機結構缺點是計算速度慢,流水線結構雖然占用資源相對較多,但對于現有FPGA芯片資源來說并不是問題,且運算速度快,可以實現高速實時處理,流水線單步迭代結構如圖3所示。
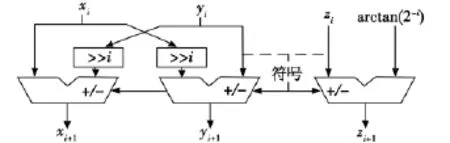
圖3 CORDIC流水線單步迭代結構Fig.3 Single step interation structure of CORDIC pipeline implementation
由于CORDIC算法旋轉的角度范圍為-99.9°~99.9°,不能達到 NCO 和鑒相器角度范圍 -180°~180°的要求。因此,需要在初次迭代前增加一個特定的“起始”步驟來擴大角度覆蓋范圍,根據三角函數的對稱性,如果輸入的數處于第一、四象限,則第一步不需要旋轉,如果處于第二、三象限,則需旋轉+180°或-180°。NCO采用8級迭代加1級初始角度旋轉運算,仿真結果如圖4所示,鑒相器和AM解調關鍵模塊采用9級迭代加1級初始角度旋轉運算,仿真結果如表1所示。
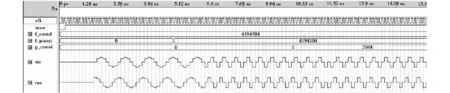
圖4 NCO仿真結果Fig.4 Simulation of NCO

表1 鑒相器和AM解調關鍵模塊仿真結果Table 1 Simulation of phase detector and key module of AM demodulation
在NCO中,采樣頻率fs=8 MHz,載頻fL=1MHz,頻率控制字位數N為25位,相位控制字位數M為12位,頻率控制字為f_con=2N·fL/fs=4194304,輸出正余弦樣本位數為10位,從圖中可以看出,頻率偏移控制字和相位控制字可以靈活調整本地載波的頻率和相位。
鑒相器和AM解調關鍵模塊中,輸入為10位,輸出相位為12位,輸出幅度為18位,其中8位表示小數,從表中可以看出,鑒相的誤差在0.3°以內,AM解調的誤差在0.1 mV以內。
根據CORDIC算法的原理和實現過程,如要求提高精度,可通過適當增加迭代次數和處理器字長,但這會降低運算速度,所以必須在這兩者之間進行權衡。
當初始頻差為20 kHz、初始相差為90°、信噪比為10 dB時,將在QuartusII8.0中仿真的結果保存為.tbl格式數據文件,用Matlab軟件讀取.tbl文件進行波形顯示[11]。圖5給出了改進Costas環與傳統Costas環相位抖動的比較,從圖中可以看出,改進Costas環相位抖動誤差在2°左右,相對傳統Costas環的4°誤差有了很大提高,精度提高的代價是捕獲時間變長,但只要滿足832 μs的指標要求即可。另外,改進Costas環的另一優點是捕獲帶寬,可以達到±100 kHz,圖6給出了頻差為100 kHz,信噪比為10 dB時由改進Costas環解調出的數字基帶信息為111010010100,其中前5位為巴克碼,后7位為仰角功能識別碼,完全符合要求。
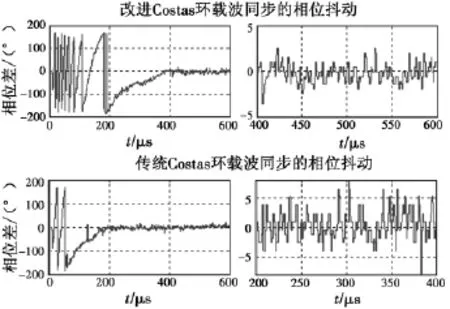
圖5 頻偏20 kHz、相差-90°、信噪比10 dB時的相位抖動Fig.5 Simulation of phase jitter when frequency difference is 20kHz,phase difference is-90°and SNR is 10 dB
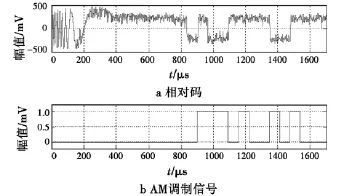
圖6 2DPSK信號解調仿真結果Fig.6 Simulation of 2DPSK demodulation
圖7給出了頻差為100 kHz,信噪比為10 dB時的AM解調仿真結果,可以看出,較好地完成了MLS掃描信號的包絡解調。
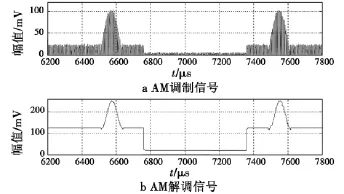
圖7 AM解調仿真結果Fig.7 Simulation of AM demodulation
5 結束語
對Costas環進行了改進,捕獲帶較寬,相位抖動幅度小。數控振蕩器、鑒相器和AM解調關鍵模塊采用CORDIC算法設計,易于FPGA實現,利用同一電路完成MLS信號的2DPSK解調和AM解調,仿真結果表明,精度高、速度快、具有較高的工程應用價值。
[1]弋沛琦,高瑞乾,劉石源.飛機著陸系統的現狀與發展[J].海軍航空工程學院學報,2005,20(4):461-464.
[2]張欣.擴頻通信數字基帶信號處理算法及其VLSI實現[M].北京:科學出版社,2004.
[3]林海都,高強.基于FPGA的全數字Costas環的設計與實現[J].電子技術應用,2007,33(10):34-36.
[4]周其煥,魏雄志,崔紅躍.微波著陸系統[M].北京:國防工業出版社,1992.
[5]駱艷卜,張會生,張斌.一種CORDIC算法的FPGA實現[J].計算機仿真,2009,26(9):305-307.
[6]郭立浩,段哲民,白森.采用CORDIC算法的直接數字頻率合成器的設計[J].電光與控制,2006,13(5):77-79.
[7]王淵,黃穎.基于反正切相位檢測的Costas環分析及FPGA 實現[J].通信技術,2010,43(8):124-126.
[8]余建宇,羅丁利,陳矛.基于CORDIC算法的數字鑒頻方法及其在FPGA中的實現[J].火控雷達技術,2007,36(3):72-77.
[9]胡海華,楊芳,時華杰.基于CORDIC算法的AM基帶解調方法[J].數據通信,2010(3):38-41.
[10]許建華,劉美娟,張超.基于CORDIC算法的數字中頻檢波技術研究[J].中國電子科學研究院學報,2007,2(5):531-535.
[11]王旭東,潘廣楨.MATLAB及其在FPGA中的應用[M].北京:國防工業出版社,2006.

