基于魯棒優化算法的小型無人機模糊控制器研究

孫大偉， 許國棟

(中國空空導彈研究院，河南 洛陽 471009)

0 引言

模糊控制器的應用是現代控制理論中一個比較重要的研究方向，特別是在飛行控制課題中，當飛行器發生飛控傳感器失靈、性能參數指示不精確、外界紊流的干擾等特殊情況時，利用模糊控制技術來提高整體系統的適應性和可靠性，已成為提高飛行器安全性能的一種十分有效的解決手段。歐美［1-4］和俄羅斯［5］科學家在飛行控制系統內結合模糊控制技術的研究上都取得了長足的進步，一些研究成果已在小型無人飛行器(SUAV)上得到應用。

1 魯棒H2/H∞優化算法簡介

從文獻［2-3］可知，模糊控制器的構造一般都參照經典(Crisp)控制器的結構原理，其中包括微分和積分動態反饋，以及為經典控制器求取的增益系數，都可以被轉換到模糊控制系統中。典型的控制系統最優系數求解方法如文獻［6］，其離散模型的標準形式如圖1所示。

圖1 無人機離散模型Fig.1 Discrete model of SUAV

外部擾動向量g(渦流速度隨機向量)為Dryden模型［7］，為了通用化將此模型轉化成了多維成形濾波器形式，其輸入由白噪聲η激發。成形濾波器的狀態空間為四子集矩陣［Af，Bf，Cf，Df］只有在隨機擾動時被啟用。矩陣B0g將控制輸入u和擾動輸入g結合為一個控制輸入向量A為SUAV的狀態空間矩陣，C0為輸出向量Z的觀測矩陣，而Z被用來計算系統控制品質，而Cc為真實閉環系統輸出Y的觀測矩陣。成形濾波器DE為離散開關，周期為Ts，連續型被控對象的閉環系統為四子集矩陣［A，B0g，Cc，Dc］，另一個四子集矩陣［A，B0g，C0，D0］被用來做最優化判斷。SUAV 縱向運動的狀態向量 X=［v，α，q，?，h］T，包括真空速、攻角、俯仰角速度、俯仰角和高度。觀測兩類SUAV應用模型:標稱模型(無擾空速vnom)和參數擾動模型(受擾空速vpert)，為了計算這兩類模型的控制品質和魯棒性，采用了H2/H∞魯棒優化算法。

定常擾動下離散系統每個模型(標稱和參數擾動)的H2范數為

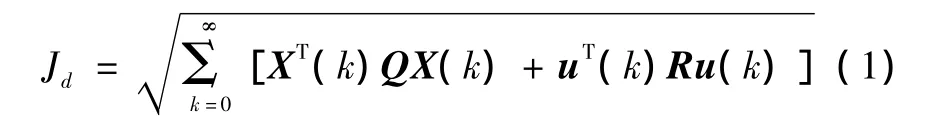
隨機擾動下每個模型的H2范數為

每個模型的H∞范數為

式中，wN為奈克維斯達頻率，wN=π/Ts。

式(1)，式(2)中:X為狀態空間變量;u為控制向量;EM為數學期望算子;Q和R為權矩陣。式(3)中，為敏感度函數矩陣T(jw)在頻域0≤w≤wN內的最大奇異值［8］，用來計算系統魯棒性。相對于圖1，矩陣T為:T(z)=K(z)G(z)［E+K(z)G(z)］-1。式中:z=exp(jwTs);G(z)和K(z)為SUAV執行機構和調節器的傳遞函數矩陣。

可以得到Pp-r(控制品質-魯棒性)H2/H∞優化判據為

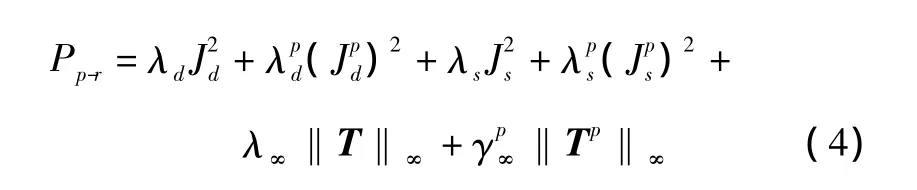
λd，，λs和 λ∞，為相應的權系數，它們被用來平衡定常和隨機擾動情況下系統控制品質和魯棒性之間的關系，式(4)反映了控制器Cn(n為優化判據的步長范數)可變參數的向量函數，此向量囊括控制器的可調節參數，執行優化的結果為

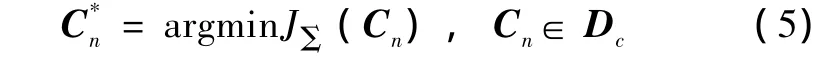
Dc為控制器參數在空間中的穩定區域。SUAV縱向運動標稱模型(vnom=250 km/h)和參數擾動模型(vpert=200 km/h)的狀態矩陣和控制矩陣為

下標“p”表示參數擾動。本SUAV的縱向運動只受控于升降舵:u=δe。經典控制器的結構如圖2所示。由俯仰角和俯仰角速度傳感器以及相應增益系數Ks和Kq組成的角度穩定通道，可以自動求出俯仰角的穩態值，而高度穩定器Wh(z)由預置輸入穩定高度。角穩定器Wα(z)和高度穩定器都是簡單的數字PD控制器。

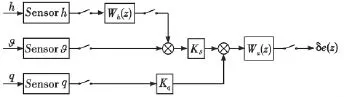
圖2 自動駕駛儀結構圖Fig.2 Autopilot of SUAV

2 模糊飛行控制器

根據文獻［2］的建議可知，為了減少飛控計算機能耗并提高系統魯棒性，可以在原型機的基礎上用模糊控制器替換上述的控制器，其結構如圖3所示。

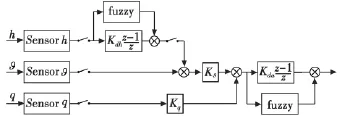
圖3 模糊飛行控制器結構圖Fig.3 Fuzzy autopilot of SUAV

圖中，fuzzy表示模糊控制器模塊，為雙輸入單輸出模糊控制器。模糊控制器的結構如圖4所示，采用三角隸屬度函數，相應的表達式為

式中:i為隸屬函數序號;a，b，c為函數頂點。而輸入信號模糊度值為

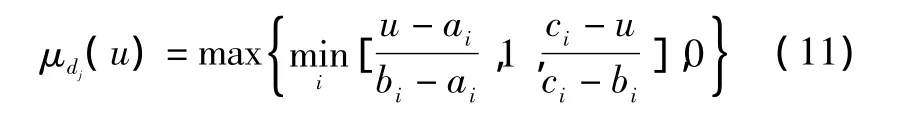
圖4 模糊控制器Fig.4 Fuzzy controller

知識庫的模糊規則根據原型控制器的數據進行規劃，并進行適當的調整。總共啟用25條規則，初始的模糊規則庫如表1所示。

表1 初始俯仰角通道模糊規則庫Table 1 Initial fuzzy logic base for pitch

為了使規則庫的控制面盡量貼合實際，在原型機控制經驗參數的基礎上，對初始模糊規則庫進行了重新規劃，規劃結果如表2。

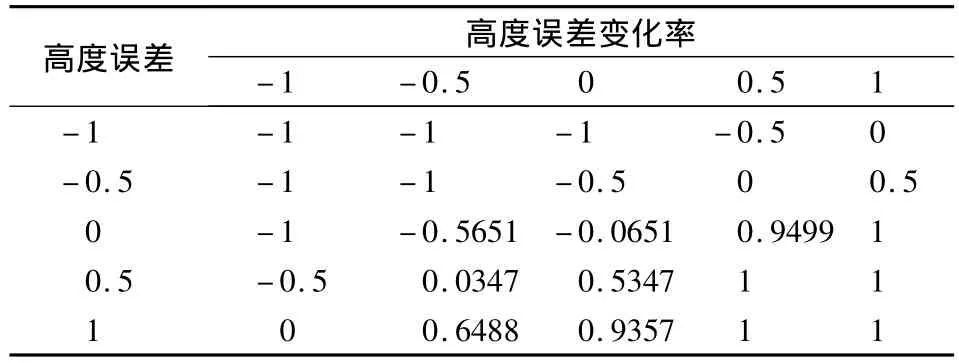
表2 處理后俯仰角通道模糊規則庫Table 2 Optimized fuzzy logic base for pitch

模糊控制器的解模糊采用重心法，表達式為

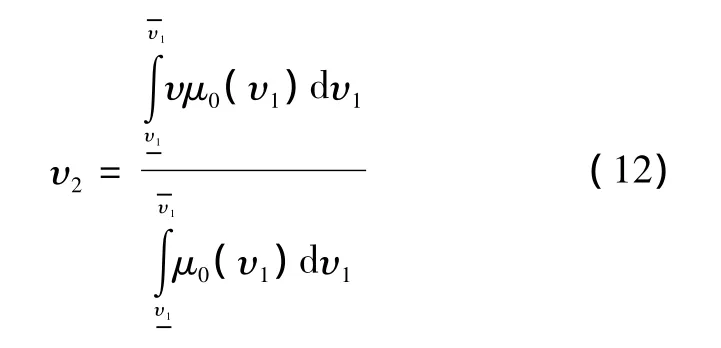
3 原型機、模糊控制器動態特性比較

在SIMULINK中，將原型控制器與模糊控制器在定常和隨機擾動情況下，分別對SUAV縱向運動控制系統的標稱和參數擾動模型進行仿真分析比較，這里取了幾個主要參數，如圖5～圖10和表3～表4所示。

圖5 標稱模型高度比較圖Fig.5 Comparison of nominal model in height

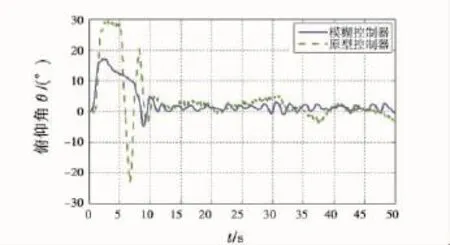
圖6 標稱模型俯仰角比較圖Fig.6 Comparison of nominal model in pitch

圖7 標稱模型俯仰角速度比較圖Fig.7 Comparison of nominal model in pitch angular velocity

圖8 參數擾動模型高度比較圖Fig.8 Comparison of perturbed model in height

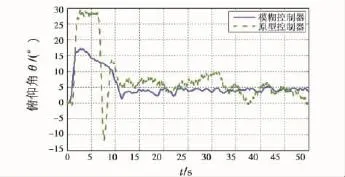
圖9 參數擾動模型俯仰角比較圖Fig.9 Comparison of perturbed model in pitch

圖10 參數擾動模型俯仰角速度比較圖Fig.10 Comparison of perturbed model in pitch angular velocity

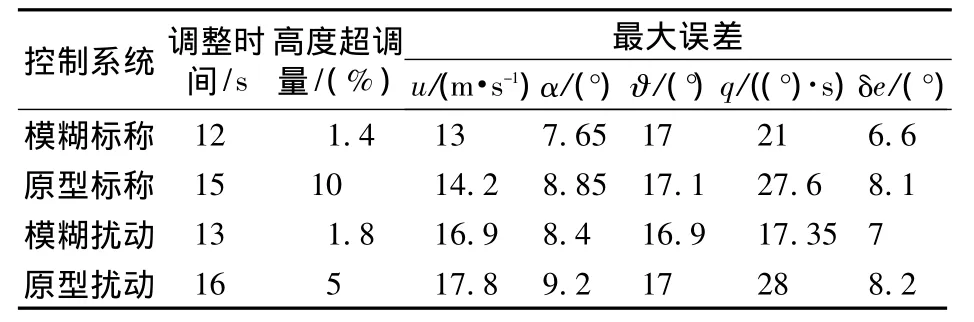
表3 定常信號下標稱和擾動系統的性能指標Table 3 Comparison of the fuzzy and crisp systems'step responses

表4 隨機信號下標稱和擾動系統的協方差Table 4 Comparison of the state variables'RMS of the fuzzy and crisp systems

4 結論

比較原型控制器和模糊數字控制器，發現在保持同一級別魯棒性的情況下，模糊控制器擁有更好的飛控品質;在定常信號下，無論是標稱模型還是參數擾動模型，模糊控制器都擁有更小的調整時間和相位差;在隨機信號下，模糊控制器能更有效地壓制外部擾動，并且所有的協方差也小一些;模糊控制器完全能滿足NPRS［9］(Nominal Performance Robust Stability)方法的要求。雖然模糊控制器的魯棒性更勝一籌，但是其模糊規則庫的優化是個難題，在后續工作中將對此開展研究。

［1］SCHRAM,G,KAYMAK U,VERBRUGGEN,H B.Fuzzy logic control［M］.New York:Berlin Springer-Verlag,1993.

［2］SCRAM G,VERBRUGGEN H B.A fuzzy control approach［M］.New York:Berlin Springcr-Verlg，1991.

［3］LIN C F.Advanced control systems design［M］.New Jersey:PTR Prentice Hall Inc,Englewood Cliffs,1994.

［4］DRIANKOV D,HELLENDOORN H,REINFRANK M.An introduction to fuzzy control［M］.New York:Berlin Springcr-Verlg，1991.

［5］УЛЬЯНОВ С В.Нечеткие модели интеллектуальных систем управления:теоретические и прикладные аспекты (обзор)［J］.Изве.АН СССР.Сер.Техническая кибернетика.1991(3):3-29.

［6］TUNIK A A,ABRAMOVICH E A.Parametric robust optimization of the digital flight control systems［J］.Proceedings of the National Aviation University.2003,17(2):31-38.

［7］MCLEAN D.Automatic flight control systems［M］.Prentice Hall Inc.,Englewood Cliffs,1990.

［8］KWAKERNAAK,H.Robust control and H∞-optimization［J］.Tutorial paper.Automatica.1993,29(2):255-273.

［9］UNIK A A,RYU H,LEE H C.Parametric optimiz-ation procedure for robust flight control system design［J］.KSAS International Journal Seoul.2001，2(2):95-107.