應答著陸系統測角方案設計

楊益歡， 趙修斌， 王 偉

(空軍工程大學電訊工程學院，西安 710077)

0 引言

應答著陸系統(Transponder Landing System，TLS)，是為適應復雜場地環境和軍用移動導航，由美國ANPC公司研制的一種基于二次雷達應答機的精密進近著陸引導系統。系統通過發射1030 MHz的高頻詢問并接收飛機應答機1090 MHz的回答信號，采用相位干涉測角原理獲取飛機的方位和仰角信息。TLS彌補了儀表著陸系統(Instrument Landing System，ILS)的不足，克服了ILS對場地環境要求苛刻的缺點，只加裝地面設備，利用飛機現有的ILS接收機和二次雷達機載設備，不對飛機進行任何改動就可在復雜場地條件和臨時機場實現精密進近著陸。例如一些自然環境惡劣的山區機場、高原機場以及處于戰略要害的軍用機場等［1-3］。

基于早期的固定式應答著陸系統在美國華盛頓州、威斯康星州、新澤西州以及澳大利亞和菲律賓蘇比克灣等地的成功使用，ANPC公司又陸續發展了針對軍用移動導航的“螢火蟲”、“犀牛”移動式應答著陸系統，但是，國內還沒有引進該設備。因此，目前啟動對TLS的研制和相關問題的研究對我國軍民用航空的發展具有積極的意義和重要的價值。

一個精密進近著陸系統的關鍵是系統角度和距離的測量，應答著陸系統主要采用相位干涉式測角和詢問回答式測距原理。其中，角度測量技術是系統的關鍵技術，傳統的應答著陸采用的是基于模擬電路的測角實現方案，測角精度相對較低。因此，根據系統測角原理設計更加合理的高精度角度測量方案，將為系統總體設計和技術實現奠定良好的基礎。

1 TLS測角基本原理

TLS采用相位干涉式測角法，兩個接收天線同時接收飛機的回答信號，不同方位上飛機應答器發射的無線電信號到兩個接收機的距離不同，因而相位也不同。只要測出它們的相位差就可確定飛機的方位(仰角)。

如圖1，假設兩個接收天線位分別于A，B兩點，它們之間的基線為d，應答信號入射角度為θ，并且RA＞＞d，RB＞＞d，若鑒相器測得飛機應答信號的相位差為Φ，應答信號的波長為λ，則有

由此可得飛機(仰角)角度為

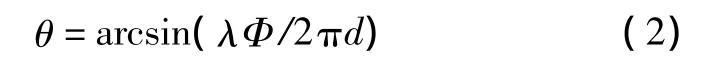
從式(2)可以看出，測量飛機應答信號到達各接收天線的相位差便是系統測角的關鍵所在，所以整個測角方案的重點和難點就是如何設計高精度的鑒相系統。

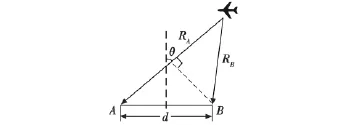
圖1 TLS測角基本原理圖Fig.1 Basic angle measurement principle of TLS

2 TLS測角技術方案

應答著陸系統的方位和仰角測量分別采用由3根天線組成的水平天線陣和由4根天線組成的垂直天線陣。根據應答著陸系統的基本測角原理，以天線陣中的一根為參考天線，分別求出其他天線與參考天線之間的相位差，便得到幾個不同分辨率的天線孔徑，然后通過解相位模糊算法得到飛機的角度信息。

隨著數字電路設計工藝和精度的不斷提高，傳統的基于模擬電路的測角方案已經不能滿足高速、高精度的測角要求。根據系統測角原理，可以采用圖2所示的數字化測角原理進行分塊實現。

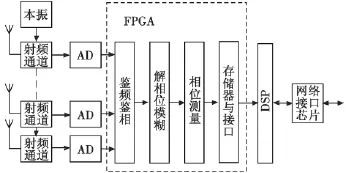
圖2 TLS測角方案總體框架圖Fig.2 The angle measurement scheme of TLS

飛機應答信號被天線陣列接收，經過射頻通道與本地振蕩器產生的1030 MHz本振信號混頻，將接收信號下變頻到60 MHz的中頻，然后以適當的頻率對中頻信號采樣量化成數字信號后，分為兩路送入FPGA進行數字鑒相和鑒頻處理，選擇1個參考通道，測量其他通道與參考通道間的相位差，對得到的各路相位差數據采用合理的算法進行相位模糊(多值性)的消除，得到精確的相位測量值，送入存儲器并在DSP處理器中解算獲取飛機方位和仰角信息;對數字鑒頻得到的頻率信息主要用來進行頻率誤差的補償。在DSP處理單元中將測量得到的飛機角度和距離信息與理想的下滑道信息相對比后，得到飛機位置偏差信息，將這些信息送入網絡接口芯片，用以太網絡的總線方式送入主機。

3 關鍵技術

3.1 數字下變頻技術

數字下變頻(DDC)［4-5］的中心思想就是將中頻A/D采樣信號與數控振蕩器(NCO)產生的本地數字中頻信號進行混頻，將其下變頻到基帶，以便于信號的后續鑒相處理。其原理框圖如圖3所示。

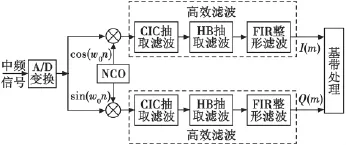
圖3 DDC原理框圖Fig.3 The principle diagram of DDC

設經過A/D變換后的輸入樣本信號為x(n)=a(n)·ej［w0n+θ(n)］，將其展開可得

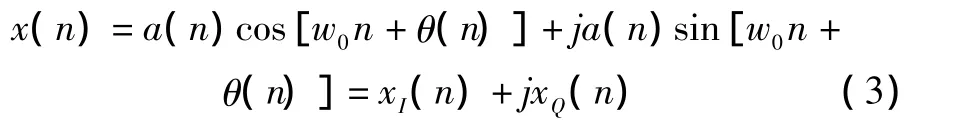
式中:xI(n)，xQ(n)分別表示輸入樣本的實部和虛部;w0為信號的載頻;ejw0n為數控振蕩器的輸出。根據頻移特性，混頻后信號x(n)的頻譜被搬移到了基帶，故有

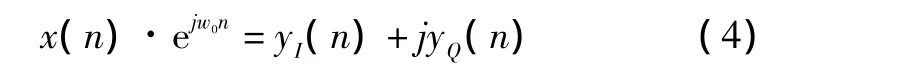
在實際工程應用過程中，輸入信號一般都是實信號，信號的虛部應當為零，即

因此混頻器的實際輸出應當為

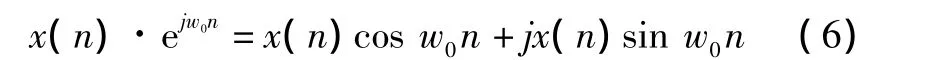
將其通過高效低通濾波器，濾除高頻分量后便得到了所需的基帶信號，以進行后續處理。

3.2 高精度的數字鑒相技術

各路應答信號經過數字下變頻到基帶以后就可以開始進行鑒相處理，在得到基帶的I、Q兩路正交信號后，采用基于坐標旋轉數字計算機(CORDIC)的算法便可以實現該路應答信號相位的獲取。

3.2.1 CORDIC 算法的原理［6-7］

CORDIC算法是1959年由J.Voider等人提出的，用一系列迭代操作完成角度的旋轉計算，每一次迭代只采用加減法和移位操作，便于任意角度旋轉的FPGA技術實現。其算法原理如下。

將向量(Xj，Yj)旋轉θ角，得到一個新的向量(Xk，Yk)，如圖4所示。

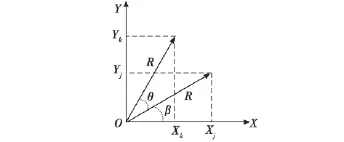
圖4 向量旋轉坐標圖Fig.4 Sketch map of vector coordinate rotation

那么有

寫成矩陣形式為

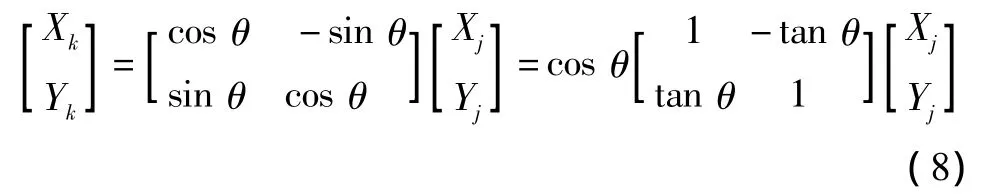
假設θ是由n個θi角度疊加而成的。即令θ=，其中di表示旋轉的方向，當順時針旋轉時，di=-1;當逆時針旋轉時，di=+1，為了便于硬件的數字實現，將每次的旋轉角度 θi加以限制，使得 θi=arctan 2-i，這樣式(8)變為

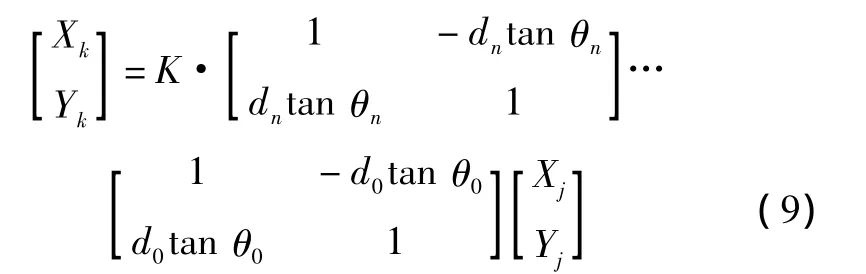
其中，K=cos θn…cos θ1·cos最終收斂于0.6073(當迭代次數趨于無窮的時候)。因此這個旋轉算法需要一個調整增益An，其值為收斂值0.6073的倒數即1.647。實際上，調整增益是取決于迭代次數的。

對于FPGA來說，式(9)中帶tan項的乘法操作就可以被簡化為n次簡單的移位操作。通過一系列基本角度單元實現，可完成任意角度的旋轉。

從式(9)可見，每一次迭代旋轉可以表示為

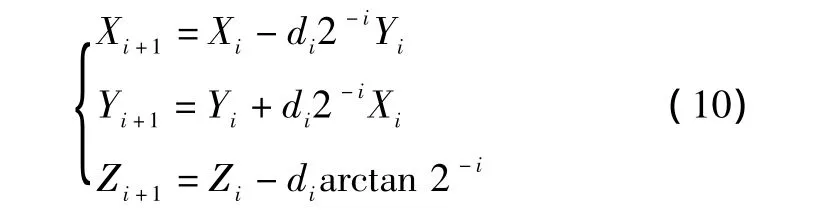
其中，Zi+1表示每一次迭代后的累加角度。

在向量化模式下，CORDIC旋轉器對輸入向量進行必要角度的旋轉，使得向量最終調整到x軸上。即第i次旋轉的角度為arctan 2-i，旋轉的方向由Yi決定，若 Yi＜0，則 di=+1;若 Yi＞0，則 di=-1，最終使Yi→0。式(10)迭代的最終結果為

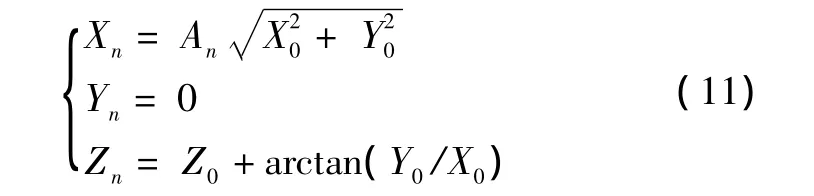
在式(11)中，令角度累加器的初始值Z0=0，則有Zn=arctan(Y0/X0)。即當迭代完成時，Zn的值即為初始輸入X0、Y0的反正切值。

3.2.2 鑒相器設計

經過數字下變頻后，可將每1路應答信號都分解為I、Q兩路的正交信號，如果將兩路正交信號相比，即可得到該路信號相位的正切值，再利用CORDIC算法的原理就可以得到每路信號的精確相位，然后求解各路相位差并作解模糊處理就可得到精確的相位差。TLS數字鑒相的設計方案如圖5所示。

圖5 TLS數字鑒相原理框圖Fig.5 Digital phase detection principle of TLS

以方位天線測角為例，每個陣元接收到的應答信號都可以分解為兩路正交信號，經過CORDIC算法以后可以得到φ1、φ2、φ3三個不同的相位，以其中一個作為參考(如 φ1)，通過比較器計算出 φ2、φ3與 φ1之間的相位差Φ1、Φ2，并將其送到基站計算機的FPGA模塊進行解相位模糊處理，得到精確的相位差Φ。再通過式(2)即可準確地計算出飛機的方位信息。

因此，如何設計快速有效的CORDIC算法的結構將是整個鑒相過程的關鍵。CORDIC算法主要有簡單狀態機和高速全流水線結構［8］。簡單狀態機結構主要采用折疊/迭代方式，在每個周期內都將精確地計算一次式(10)的迭代，計算速度慢，迭代時設計的筒形移位器復雜。流水線CORDIC結構雖然占用的硬件資源較多，但是流水線結構可以提高數據的吞吐率，從FPGA發展趨勢看，芯片內的門資源相對富裕，對流水線CORDIC的實現規模約束較小，流水線結構不存在迭代式CORDIC的反饋回路，使得單元結構更加規則，有利于FPGA實現。

考慮到系統的實時性和時效性，鑒相器采用圖6所示的CORDIC流水線結構［9-10］來進行硬件實現。

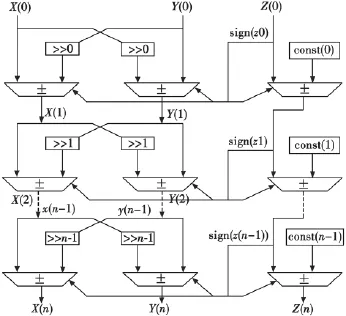
圖6 鑒相器CORDIC算法的流水線結構圖Fig.6 Pipelining diagram of CORDIC algorithm

如圖6，將xI(n)、xQ(n)分別看作是X(n)和Y(n)，并取Z(0)=0，經過上述流水線結構迭代n次后使得Y(n)=0，此時得到的Z(n)的值就是所需的每路應答信號對應的相位值。

4 仿真分析

根據以上分析和鑒相器原理，通過QuartusⅡ軟件可以設計出鑒相器的功能模塊［11］。

根據應答著陸系統的信號格式，模擬兩組經過中頻接收和數字下變頻后的信號數據分別輸入到FPGA實現的鑒相器程序，并在CORDIC算法上采用12位數據進行多次迭代，將每次的仿真結果與理論值比較得到多個鑒相誤差值，再通過求算術平均的方法就可得到迭代次數與鑒相誤差的關系如圖7所示。

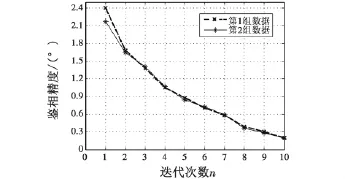
圖7 鑒相精度與迭代次數的關系Fig.7 Phase detector precision vs iteration times

可以看出，經過8次迭代后，鑒相誤差就達到了(0°，0.5°)的水平，滿足了系統角度測量的要求，同時也可以看出鑒相器的精度與輸入的數據基本無關，也就是說鑒相器的穩定度較高。為了直觀起見，對兩組數據分別進行8次迭代的仿真實驗結果如圖8、9所示。

圖8 TLS高精度鑒相器仿真結果1Fig.8 Result 1 of TLS high precision digital phase detector simulation

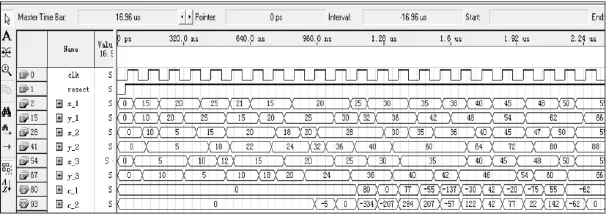
圖9 TLS高精度鑒相器仿真結果2Fig.9 Result 2 of TLS high precision digital phase detector simulation

圖8、圖9 中，x_1、y_1，x_2、y_2，x_3、y_3 分別表示3路信號經數字下變頻后得到的基帶數據，也是鑒相器的3路輸入，c_1、c_2分別為參考信號與其他兩路信號的相位差。圖中的數字表示的是由12位0、1序列構成的二進制數，只要根據設計程序中的對應關系就可以非常容易地獲得相應的相位差的度數。通過對8次迭代結果的分析，雖然輸出的兩路相位差存在時延，但是最大時延只有960 ns，對整個角度測量過程沒有影響。對比仿真結果與理論值得到的誤差為0.4°，符合圖7所示的曲線關系。因此，該設計方案既能夠達到系統所需的測角精度，同時又說明了本設計方案的可行性和有效性。

5 結束語

筆者在分析TLS測角基本原理的基礎上，設計了數字電路測角系統的實現方案。根據設計方案，重點分析了數字下變頻和高精度數字鑒相等關鍵技術及其實現方法。以FPGA為基礎，通過流水線結構的CORDIC算法實現了應答信號的鑒相過程，并在QuartusⅡ環境下進行了方案的計算機仿真，仿真結果證明，該方案不但能夠滿足系統角度測量的精度要求，而且易于實現，說明了該設計方案是可行、有效的。

［1］于向東.適于地形復雜機場的應答著陸系統［J］.國際航空，2004，24(9):52-53.

［2］駱慈孟，徐勇.TLS-跨世紀的精密進近導航系統［J］.民航經濟與技術，1994，26(8):30-31.

［3］WINNER K.Application of the Transponder Landing System to Achieve Airport Accessibility［EB/OL］.2010-10-22.http://www.ANPC.com.

［4］粟欣，許希斌.軟件無線電原理與技術［M］.北京:人民郵電出版社，2010.

［5］姚元飛，佟力，嚴國榮.S模式機載應答機的中頻數字化處理［J］.電訊技術，2009，49(6):70-73.

［6］嚴平，汪學剛，錢路.一種基于CORDIC算法的高速高精度數字鑒相器［J］.電訊技術，2008，48(4):76-79.

［7］張天瑜.低復雜度的改進型CORDIC算法研究［J］.陜西科技大學學報，2009，27(5):93-99.

［8］駱艷卜，張會生，張斌，等.一種CORDIC算法的FPGA實現［J］.計算機仿真，2009，26(9):305-307.

［9］楊宇，毛志剛，來逢春.一種改進的流水線CORDIC算法結構［J］.微處理機，2006，8(4):10-13.

［10］郭立浩，段哲民，白森.采用CORDIC算法的直接數字頻率合成器的設計［J］.電光與控制，2006，13(5):71-79.

［11］王金明，周順.數字系統設計與VHDL［M］.北京:電子工業出版社，2010.