基于SVM決策樹的網絡流量分類

邱 婧， 夏靖波， 柏 駿

(空軍工程大學電訊工程學院，西安 710077)

0 前言

隨著互聯網的不斷發展，許多新的網絡服務(如P2P、在線游戲等)采用動態端口、協議加密以及其他方面的原因，使得傳統的基于端口和基于有效載荷分析的流量分類方法已不能保證完全精確的網絡流量分類和統計。近年來，一些學者使用機器學習的方法來進行流量分類的研究。對網絡流量分類使用機器學習技術的思想在入侵檢測的研究中被首次提出［1］;文獻［2］提出一種無監督的機器學習方法來識別不同網絡應用的框架，用流的統計特性作為流的特征來進行網絡流量自動分類研究;文獻［3］和文獻［4］使用基于貝葉斯分類器和大量的流屬性來進行網絡流量的分類研究。

支持向量機(SVM)方法是一種建立在統計學習理論基礎之上的機器學習方法，該方法一方面利用非線性變換將樣本空間的分類問題轉化為高維特征空間的分類問題，有效避免冗余屬性和無關屬性對分類結果的影響;另一方面又根據結構風險最小化原則，將分類問題轉化為在特定約束條件下尋找最優超平面的二次尋優問題，從而避免分類模型對樣本先驗概率的依賴，可以有效提高分類模型在小樣本情況下的分類準確率和穩定性。目前已有學者將SVM用于網絡流量分類，并取得了較好的分類效果［5-6］。但是SVM在網絡流量分類中還存在以下問題。1)SVM本質上是2值分類，而流量分類是多類分類問題，目前基于支持向量機的多類分類算法主要是通過建立多個兩類分類器的方法，主要有“一對一”算法、“一對多”算法。但“一對一”和“一對多”算法在求解時，由于本身的算法機理問題，往往會出現無法識別區域，即在這個區域中的數據樣本，要么無法確定它們的類別，要么屬于多個類別。總之，無法將其唯一判至某類，從而出現拒識。2)由于是通過將多類問題轉為兩類問題解決，“一對一”算法和“一對多”算法分別需要構造k(k-1)/2和k個支持向量機子分類器，從而造成樣本訓練時間長，計算復雜，決策時間慢，影響了分類效率。

本文提出了一種基于SVM決策樹的網絡流量分類方法，該方法充分利用SVM決策樹方法代價低、速度快、精度高等優點，可以有效提高分類模型的整體性能。

1 原理與方法

1.1 SVM決策樹主要思想

在多類分類問題中，類間分布會出現“類簇”的情況。所謂“類簇”是指多類樣本空間分布局部集中可以將其看作一個新集合類，即形成所謂的“簇”。在訓練初期每一個樣本都看作一個類簇，通過不斷合并樣本類更新類蔟。例如圖1a四類樣本兩簇，Class3和Class4的空間分布出現局部集中的現象，則可以將Class3和Class4看作一個簇，同理Class2和Class1也出現空間分布局部集中的現象，則同樣也可以將Class2和 Class1看作一個簇;圖1b四類樣本先把Class3和Class4看作一個簇，因為Class3和Class4相對整體來講是局部集中的，即Class3和Class4形成一個新簇Cluster5，然后新簇Cluster5與Class1合并為一個新簇Cluster6。

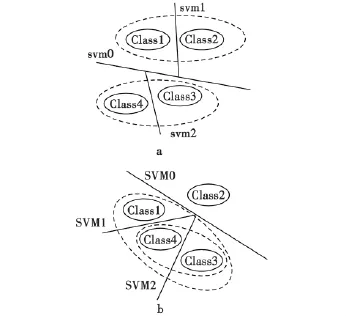
圖1 類間類簇示意圖Fig.1 Schematic diagram of between-class clusters

SVM決策樹的多類分類算法是基于類簇展開的，該方法的基本思想是:首先將所有類別分成兩個子類，再將子類進一步分成兩個次級子類，如此循環下去，直到得到一個單獨的類別為止，這樣就得到一棵倒立的二叉樹，然后對每個決策節點的兩類分類問題用SVM解決，該方法的特點是逐步把某一類從其他類分開［7］。SVM決策樹有兩種實現類型(以4個類別為例)。1)正態樹。從頂層開始，每個節點分類器將類的集合劃分成兩個類的子集合，直到底層的節點分類器將某一類或某兩類劃分開來。2)偏態樹。每一節點分類器將某一類與其他類別分開，最底層的節點分類器將最后剩下的兩類分開。如圖2所示，這兩種分類器的構造代價相當。

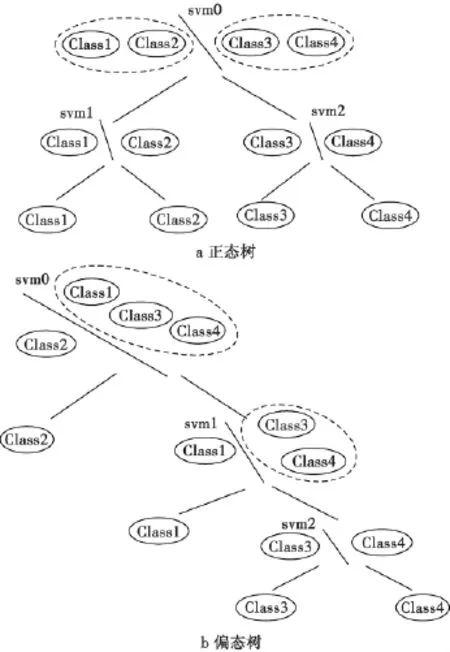
圖2 SVM決策樹構型Fig.2 SVM decision tree configuration

對于N類問題構造一棵二叉決策樹，則樹的每一個葉子節點對應一種類別，每一個度為2的非葉子節點對應一個子SVM分類器，所以決策樹共有2k-1節點，葉節點個數為k，只需構造k-1個SVM分類決策函數，具有較高的分類效率，也不存在拒識區域。

1.2 類間分離測度

在設計SVM決策樹時，可以考慮將容易分(不易產生錯分)的類先分離出來，然后再分不容易分的類，這樣就能夠使可能出現的錯分盡可能地遠離樹根。要使每個決策節點的類間隔盡可能大，首先要根據訓練樣本集估計各類間的分離測度［8］。所謂類間的分離測度，是對類與類之間的可分程度大小的一個度量，它表示類與類的遠離程度。分離測度大，說明這兩類比較容易分開。一般情況下，將類i與其余各類間的最小分離測度作為類i的分離測度)，即類的分離測度，其中，sij表示類 i與類j之間的分離測度。

其中，dij(i=1，2，…，k)表示類 i和類 j中心距離

ci是根據訓練樣本計算出的類中心，表示為

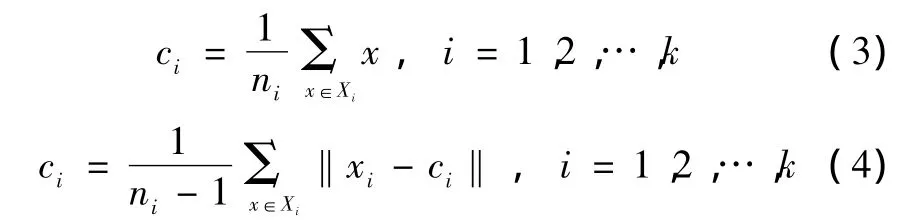
其中:ni為類Xi中的樣本個數;σi表示類i的標準差;σj表示類j的標準差，其表示類的分布情況。

而對于非線性的訓練樣本集，經非線性映射Φ作用后，在特定空間H中類i和類j間的分離性測度為

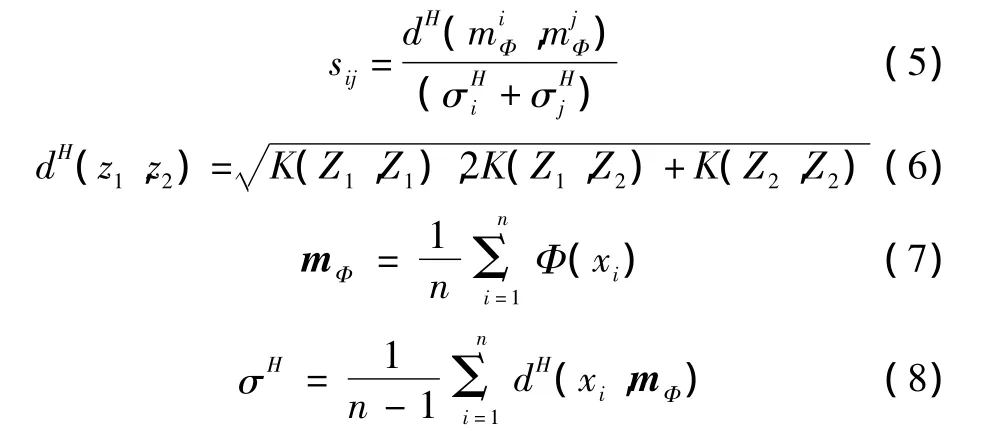
其中:K(·，·)為核函數;dH(Z1，Z2)為經非線性映射作用后，在特征空間H中訓練樣本間的歐氏距離;同時輸入空間樣本的中心經映射后得到不再是特征空間中樣本的中心，特征空間樣本的中心向量為mΦ，n為樣本的個數;σH為特征空間中的類方差。

當i≠j，sij表示類i與其他類之間的分離性測度，sij數值越大，則類i和類j間的分離性越好。當 i=j，max(sij)對應的類i為最易分的類。相反，min(sij)對應的類i為最難分的類。SVM決策樹將類間分離度測度引入，更精確地評定類間分離難易程度。

1.3 算法步驟

SVM決策樹在具體算法實現上分為訓練和分類兩個過程。訓練過程借助類間分離測度的概念，逐層合并類簇，進行訓練建模。而SVM決策樹分類過程是訓練建模的逆過程，結合決策樹的方法，從決策數的根節點到葉節點逐層判斷最終獲取測試數據所屬類別。

對于訓練過程，假設對于N類問題，訓練集合Φ={X1，X2，…，XN}:

1)計算樣本數據中各類的分離測度si，i=1，2，…，N;

2)將分離測度按降序排列，設sm1≥sm2≥…≥smk;

3)設計數器k=1;

4)構造子分類器SVMk的訓練集Φk=Σ1+Σ2;其中Σ1={(Xmk，+1)}，Σ2={(Y，-1)|y∈{Φ -{Xmk}};按兩類問題構造分類器SVMk;

5)調整訓練集和計數器，Φ=Φ-{Xmk}，k=k+1;

6)重復步驟4)和步驟5)，直到構造完第N-1個子分類器SVMN-1。

按照此方法構造的決策樹具有層次結構，每個層次的子SVM最多一個，且重要性也不同，越靠近樹根的SVM越重要，訓練集合的元素個數也越多［9］。

分類過程則首先在根節點利用SVM分類測試樣本，若屬于左節點，則判斷該節點是否為葉節點;若是，則對待分樣本賦以該節點類別，若不是，則利用該節點的SVM進行判決，確定待分樣本屬于下一級左節點還是右節點，再判斷左節點或右節點是否為葉節點，若是，則將待分樣本賦以左節點或右節點類別。直到葉節點層級為0，即找到所屬類別。

2 實驗結果與分析

2.1 實驗工具

本文所使用的數據分析工具主要是 Weka3.6.1［10］，它是由新西蘭懷卡托大學Witten教授等人開發的開源工作平臺，是當前最著名的數據挖掘算法工具集之一，包含決策樹、支持向量機、貝葉斯分類器等多種機器學習算法。因為開源，用戶可以使用自己的代碼進行開發，并提供Java接口，便于用戶編寫新的算法用以驗證。

2.2 實驗數據

本文采用了Andew Moore等人在參考文獻［3］中所用的實驗數據集［11］。數據集中包含377526個網絡流樣本，分為10種類型。每種類型所包含的應用名稱、每類網絡流的數量和所占的比例如表1所示。

表1 實驗數據集的統計信息Table 1 Experimental data set

數據集利用TCP TRACE等工具提取了不同的TCP屬性特征，其中每個樣本都是從一條完整的TCP雙向流抽象而來，包含249項屬性特征，其中最后一項屬性是目標屬性，指明了該雙向流的類型，其他248種網絡流屬性的具體描述可以參見文獻［11］。

2.3 實驗結果及分析

首先將實驗數據集均分為兩個數據子集，分別是Set1和Set2，在這兩個數據子集中每類樣本的比例與原數據集保持一致。再從Set1中分別抽取每類應用10%(至少1個)的樣本構成訓練集，由于在原數據集包含的249項網絡流屬性中，存在眾多的冗余屬性和無關屬性，這些屬性的存在不僅會降低分類模型的準確率，而且會大大加重分類模型的計算負載，實驗中首先使用FCBF方法對訓練數據集進行過濾。然后將SVM決策樹分類算法編寫到Weka3.6.1中，通過Weka調用libSVM中的SVM多類分類算法(“一對一”和“一對多”)以及新編入的SVM決策樹算法分別對Set1進行訓練，再用Set2進行測試。測試包括分類性能和訓練時間，分類性能用召回率和準確率來評價。其中準確率刻畫的是分類器給出類別為ki的預測中正確結果的比例;而召回率則代表了本應是類別ki的實例被正確預測的比例。表2給出了采用普通SVM多類分類方法和SVM決策樹方法進行流量分類實驗的結果。

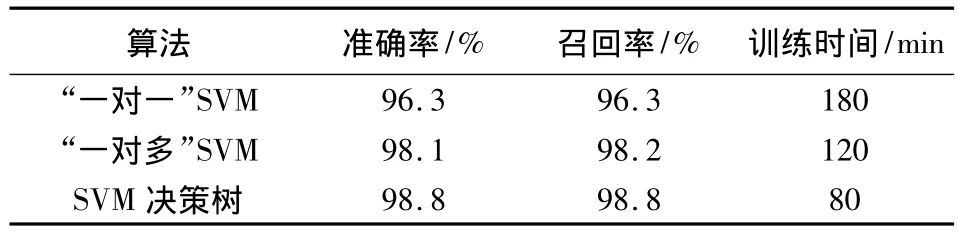
表2 分類性能和訓練時間對比Table 2 Classification performance and training time

從上面實驗的結果來看，SVM決策樹在分類性能上略高于“一對一”和“一對多”算法，在訓練時間上明顯優于“一對一”算法，下面是對實驗結果的分析:

1)SVM決策樹的子分類器采用逐層分類結構，而“一對一”和“一對多”算法的各個子分類器是平級關系，這樣SVM決策樹能夠逐級將輸入樣本最終劃分到所屬類別，充分回避了分類矛盾，提高了分類性能;

2)訓練階段，“一對一”和“一對多”算法分別需要產生k(k-1)/2，k個分類器，SVM決策樹只需要產生k-1個分類器，因此SVM決策樹算法的訓練時間較“一對一”和“一對多”算法要短;

3)SVM決策樹算法中引入了類間分離測度，最大程度地減少了積累誤差，進一步提高了分類準確性。

3 結束語

本文提出使用SVM決策樹研究網絡流量分類問題，通過在公開數據集上進行訓練與測試，實驗結果表明SVM決策樹方法的分類準確率可以達到98%以上，訓練時間也較另外兩種SVM多類分類算法短。由于網絡流量分類是流量管理和控制的前提，所以要求分類具有一定的實時性。研究在滿足一定分類準確率的條件下，如何進一步減少子分類器個數，以此減少計算量，提高分類速度，是下一步工作的重點。

［1］FRANK J.Machine learning and intrusion detection:current and future directions［C］//Proceedings of the National 17th Computer Security Conferece,1994:256-270.

［2］ZANDER S,NGUYEN T,ARMITAGE G.Self-learning IP traffic classification based on statistical flow characeristics(poster)［C］//Proceedings of the Passive Active Measurement Workshop,Boston,USA,2005:250-257.

［3］MOORE A W,ZUEV D.Internet traffic classification us in bayesi ananalysis techniques［C］//Proc eding of the 2005 ACM SIGMETRICS.International Conference on Measurement and Modeling of Computer Systems，New York:ACM,2005:50-60.

［4］ZUEV D,MOORE A.Traffic classification using a statistical approach［C］//Proceedings of the 6th International Workshop on Passive and Active Network Measurement,2005:321-324.

［5］林森，徐鵬，劉瓊.基于支持向量機的流量分類方法［J］.計算機應用研究，2008，25(8):2488-2490.

［6］徐鵬，劉瓊，林森.基于支持向量機的Internet流量分類研究［J］.計算機研究與發展，2009，46(3):407-414.

［7］BERURETT K P.Decision tree construction via linear ptogramtning［C］//The Midwest Artificial Intelligence and Cognitive Science Society Conference,Utica,1992:92-101.

［8］夏思宇，潘泓，金立左.非平衡二叉樹多類支持向量機分類方法［J］.計算機工程與應用，2009，45(17):167-169.

［9］韓家新，何華燦.SVMDT分類器及其在文本分類中的應用研究［J］.計算機應用研究，2004(1):23-24，43.

［10］WITTEN I H,FRANK E.Data mining:practical machine learning tools and techniques［M］.2nd ed.Amsterdam:Elsevier Inc,2005.

［11］MOORE A W,ZUEV D,CROGAN M.Discriminators for use in flow-based classification,RR-05-13［R］.London:Queen Mary University of London,2005.