傳遞對準中時間延遲誤差補償與濾波模型
吳訓濤,高青偉
(1. 91550 部隊,遼寧 大連 116023;2.海軍航空工程學院 指揮系,山東 煙臺 264001)
慣導系統傳遞對準中主要的誤差源包括載體撓性誤差、桿臂速度誤差、數據傳輸延遲誤差以及慣性元器件誤差等[1]。由于傳遞對準卡爾曼濾波算法的實現是在子慣導系統中進行,這就需要將主慣導系統的一些相關信息(主要是速度和姿態信息)傳輸到子慣導系統,由于傳輸延遲的存在,導致傳遞對準誤差。另外,對于平臺式主慣導系統,傳感器測量也需要一定的反應時間,從而導致測量信息的延遲。研究傳輸延遲的建模和補償對提高慣導系統初始對準精度具有重要的意義。
卡爾曼濾波技術是對慣導系統進行傳遞對準最常用的一種有效方法。然而,為使卡爾曼濾波器具有最優性能,必須使卡爾曼濾波器模型和噪聲統計特性具有準確的先驗信息[2]。對于實際的慣導系統而言,往往存在著各種不確定性誤差,若利用卡爾曼濾波器進行估計,導致濾波發散。
為解決這一問題,出現了許多自適應卡爾曼濾波算法,主要包括Sage-Husa 自適應濾波算法、模糊自適應卡爾曼濾波和衰減記憶卡爾曼濾波等。文獻[3 -5]給出了衰減因子的自適應估計方法,具有一定的理論指導意義。本文提出了一種最佳自適應估計衰減因子的方法,可在線快速計算出衰減因子的估計值,將其應用于慣導系統的傳遞對準中,仿真結果優于傳統的卡爾曼濾波。
1 傳遞對準數學模型
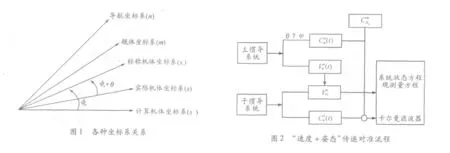
主子慣導系統誤差方程建立所涉及到的坐標系關系如圖1 所示。慣導系統傳遞對準流程如圖2 所示,利用主子慣導的速度之差作為卡爾曼濾波器觀測量之一;將主慣導的方向余弦矩陣和主慣導與標稱機體坐標系的方向余弦矩陣送入到子慣導中,計算得到姿態誤差作為卡爾曼濾波器另一個觀測量,進行狀態估計。
由于傳遞對準的時間很短,陀螺和加速度計所引起的相對速度、相對姿態誤差很小,因此在建模時不考慮這些狀態,而通過增加相對速度誤差和姿態誤差方程中的過程噪聲,以補償未建模的陀螺和加速度計測量誤差[6]。
傳遞對準濾波器的狀態變量可取為3 個相對速度誤差δVx、δVy、δVz,3 個計算機體系^s 到標稱機體系sv的相對姿態誤差,即計算失準角φmx、φmy、φmz,3 個實際機體系s 到標稱機體系sv的相對姿態誤差,即物理失準角φax、φay、φaz。由于簡化了動態模型,可增加過程噪聲來補償,將φa建模為˙φa=Wa,Wa是高斯白噪聲。傳遞對準濾波器的數學模型可所示為:
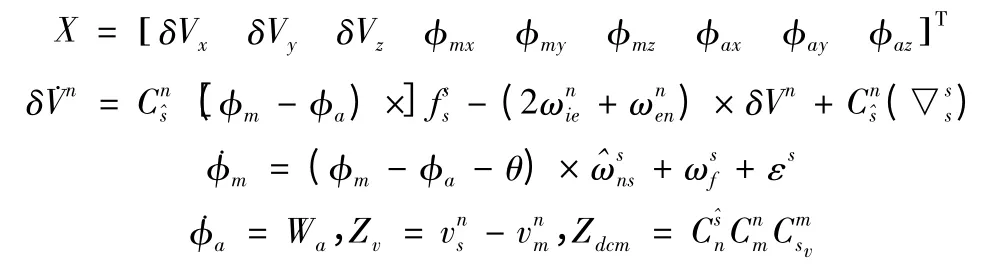
2 考慮時間延遲的量測方程
設子慣導(SINS)在t 時刻獲得主慣導(MINS)在t-Δt 時刻的數據信息,延遲時間對姿態的影響比較大,所以需要對姿態誤差觀測量進行相應的更新,當載體處于低動態時,延遲時間對速度觀測量的影響可以忽略[6]。設主慣導在t -Δt 時刻的方向余弦矩陣為則有:


同理可得:

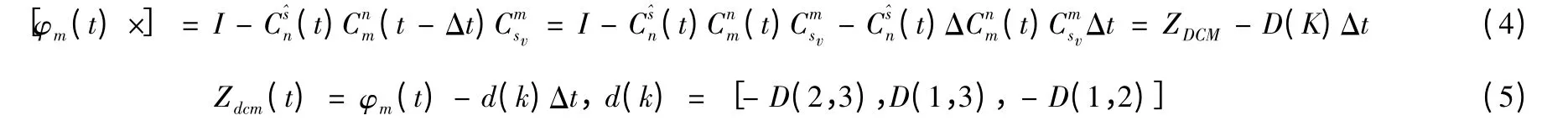
3 衰減記憶濾波器的最佳自適應算法
與常規卡爾曼濾波相比,衰減記憶卡爾曼濾波在一步預測誤差方差陣計算式中增加了一個衰減因子,加重現時測量數據在狀態估計中的作用,從而避免濾波器發散。通常衰減因子取為一個固定常數,在實際系統中,每一個誤差狀態估計程度是不一樣的,用一個衰減因子不能確切修正所有誤差狀態估計異常的情況。而衰減記憶矩陣S(k)對每一個狀態分別進行估計,從而保證衰減記憶濾波器工作在最佳狀態。為使衰減記憶濾波器工作在最佳狀態,應根據濾波器的最佳性條件在線自適應地調整衰減因子。
記估計殘差為

最佳濾波在不同時刻的殘差互不相關,用方程式表示為:
欲使Cj(k)≡0,(j≠0),須滿足:

式(9)構成了自動尋找最佳遺忘因子的基礎。
最佳衰減因子的一步算法推導:
設系統滿足條件①Q(k),R(k),P(0)均為正定對稱陣;②輸出矩陣H(k)行滿秩。
把式(8)帶入式(9)得:
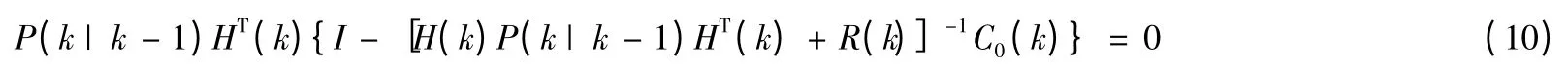
由條件①、②及式(8)知,P(k|k-1)和C0(k)均為滿秩對稱陣,因而可在式(10)兩邊左乘P-1(k|k-1)及右乘C-10 (k),整理有
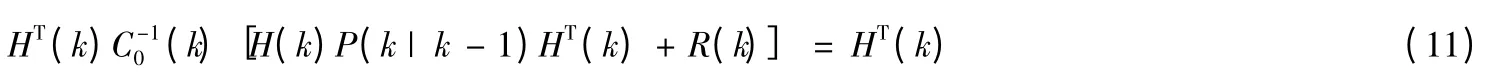
條件②已假設H(k)行滿秩,式(11)隱含式(12)成立:
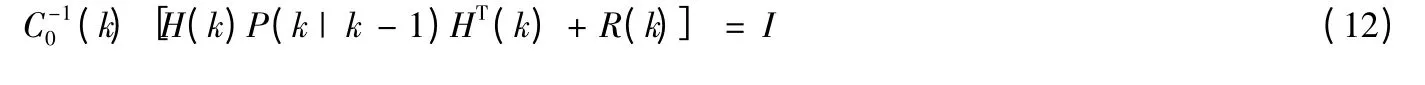
或
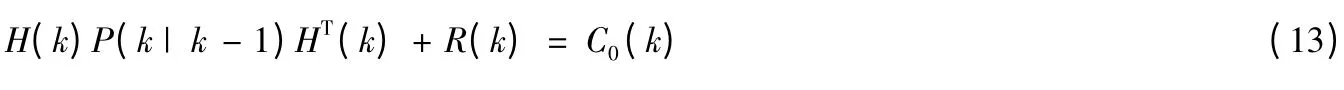
將 ( )S k 代入式(13):
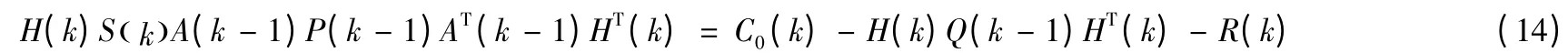

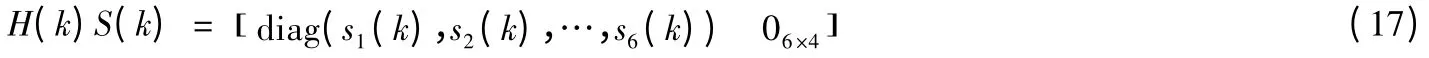
記mij(k)為M(k)的第i 行j 列的元素,記nij(k)為N(k)的第i 行j 列的元素,有
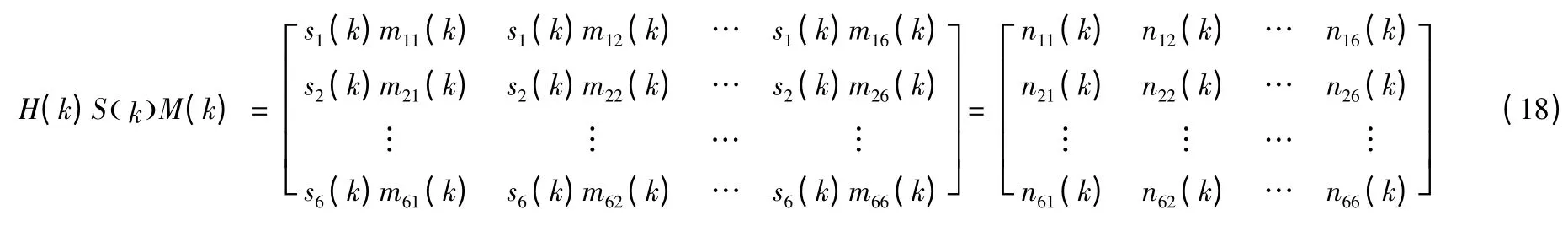
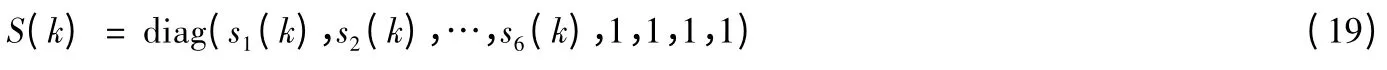
4 仿真試驗
仿真條件及參數:子慣導陀螺常值漂移為0.05°/h,加速度計的零偏為5 ×105g,3 個安裝誤差角為60',仿真時間設定為50 s,時間延遲誤差為0.03 s。
初始狀態估計值全取0,即

初始方差陣P0為對角陣,其中
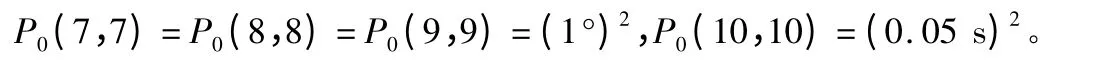
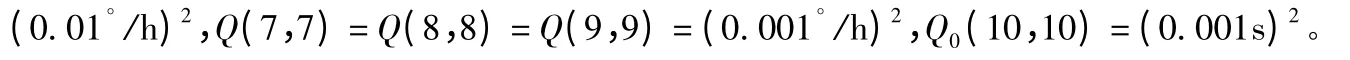
量測噪聲方差陣R 為對角陣,其中R(1,1)=R(2,2)=R(3,3)=(0.1 m/s)2,R(4,4)=R(5,5)=R(6,6)=(0.1°)2。
在P0=0.001P0,Q=0.01Q 條件下,分別用卡爾曼濾波和衰減記憶自適應濾波估計系統的狀態,固定失準角估計曲線如圖3 ~5 所示,圖中的實線和虛線分別為采用衰減記憶自適應卡爾曼濾波和常規卡爾曼濾波時的失準角估計曲線,時間延遲誤差估計曲線如圖6 所示。2 種濾波算法下的固定失準角估計誤差值如表1 所示,衰減記憶自適應濾波下的時間延遲估計誤差為0.000 4 s。
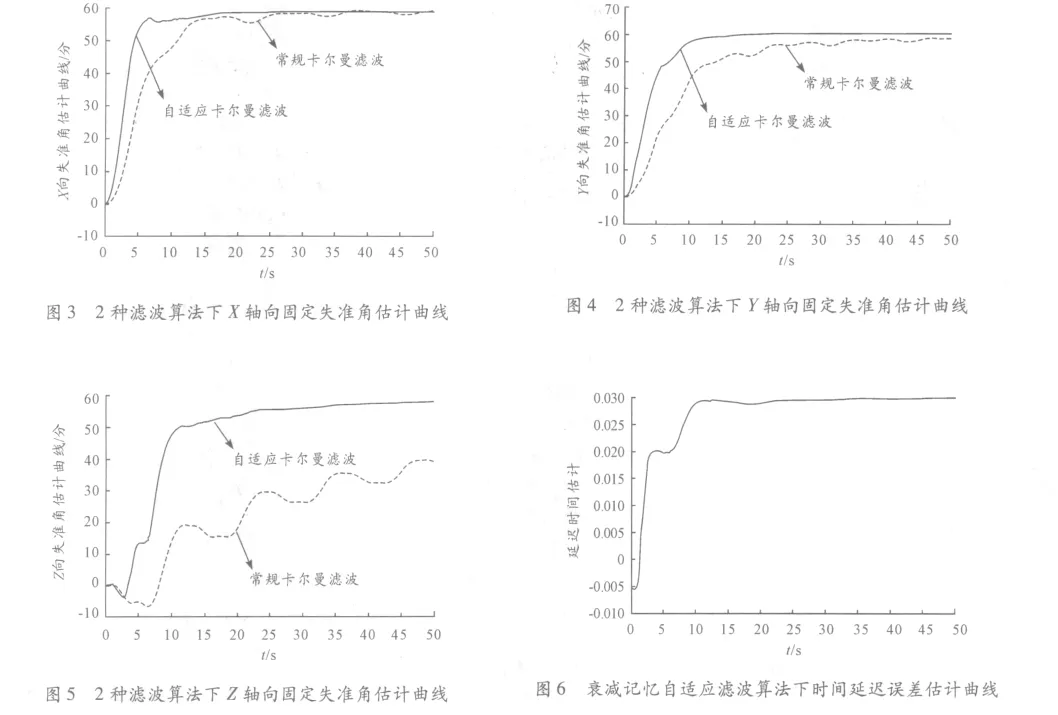

表1 2 種濾波算法下固定失準角估計誤差值
從仿真圖形和數據可以看出,衰減記憶自適應濾波在考慮時間延遲和模型與噪聲統計特性不確定性時估計固定失準角的估計精度和時間上優于常規卡爾曼濾波,水平失準角估計誤差最大為0.9',方位失準角誤差為2',時間延遲估計誤差為0.000 4 s,滿足慣導系統的傳遞對準的精度要求。
5 結論
針對傳遞對準中的時間延遲誤差進行分析,建立時間延遲下的量測方程,并建立了衰減記憶自適應卡爾曼濾波模型,采用“速度+姿態”匹配算法進行了仿真試驗,仿真結果表明,時間延遲誤差會影響失準角的估計精度和時間,采用衰減記憶自適應卡爾曼濾波可以提高傳遞對準的精度和時間。
[1]扈光峰,王艷東,范躍祖.傳遞對準中測量延遲的補償方法[J].中國慣性技術學報,2005,13(1):10-15.
[2]付夢印,鄧志紅,張繼偉.Kalman 濾波理論及其在導航系統中的應用[M].北京:科學出版社,2003.
[3]徐景碩.自適應卡爾曼濾波器漸消因子選取方法研究[J].系統工程與電子技術,2004,11(11).
[4]Xia Qijun,Rao Ming,Ying Yiqun,et al. Adaptive Fading Kalman Filter with an Application[J].Automatica,1994,30(12).
[5]Levent Ozbek,Aliev Fazil.A Comment on Adaptive Fading Kalman Filter with an Application[J].Automatica,1998,34(12).
[6]王力丹,張洪鉞,戴汝為.一種快速傳遞對準的方法[J].航天控制,2000(4):8-16.
[7]You-chol Lim,Joon Lyou. Transfer Alignment Error Compensator Design Using H∞Filter[J].Proceddings of the American Control Conference Anchorage,2002(5):8-10.

