永磁同步伺服系統(tǒng)全閉環(huán)建模及仿真

王景輝，樂貴高，霍 龍

(南京理工大學 機械工程學院，南京 210094)

永磁同步電機(PMSM)因其體積小、結構簡單、輸出轉矩大、效率高等優(yōu)點，在工業(yè)控制領域得到了廣泛應用［1］。同時PMSM 是一個非線性、多變量、強耦合的時變系統(tǒng)，因此需要建立其解耦狀態(tài)方程。1971年德國學者Blaschke 等［2］提出了矢量控制理論，使交流電機轉矩和磁通的控制實現(xiàn)解耦。近年來電機控制中普遍采用SVPWM 技術，提高了逆變器的電壓輸出能力，并保持恒定的開關頻率，特別適合數(shù)字控制。本文基于矢量控制的思想，采用電壓空間矢量脈寬調(diào)制的方法對永磁同步電機伺服系統(tǒng)進行仿真分析。

1 永磁同步電機矢量控制

以轉子為凸裝式的永磁同步電動機為例［2］得到PMSM的電壓電流、電磁轉矩和機械運動方程為:

式中:id、iq為dq 軸電流;ud、uq為dq 軸電壓;R 為定子電阻;L 為等效dq 軸電感;Pn為極對數(shù);ψf為轉子上的永磁體產(chǎn)生的磁勢;ωr為轉子機械角速度;J 為折算到電機軸上的總轉動慣量;B 為粘滯摩擦系數(shù);TL為折算到電機軸上的總負載轉矩;Te為輸出轉矩。

從式(1)可以看出，ωr、id、iq是緊密耦合的。為實現(xiàn)交流電機的解耦控制，采用id=0 的矢量控制方式，則式(1)簡化為:

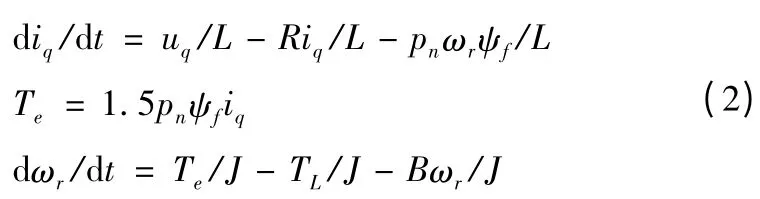
當電機軸與減速器相連，且檢測元件安裝在被控對象即減速器輸出軸上(減速器視為剛性)，組成全閉環(huán)系統(tǒng)，得到如下方程:

其中:θr為被控對象端角度輸出;i 為減速比。

由以上推導可以得出PMSM 空間矢量控制框圖如圖1所示。

圖1 永磁同步電機空間矢量控制方框圖

2 永磁同步電機全閉環(huán)系統(tǒng)建模

在Matlab/Simulink 下建立各個模塊仿真模型，步驟如下。

2.1 比例積分(PI)控制器

比例(P)控制的目的是快速調(diào)節(jié)系統(tǒng)偏差，積分(I)控制的目的是消除系統(tǒng)靜差，在Matlab 中的模型見圖2。

圖2 PI 模型

2.2 坐標變換模塊

坐標變換模塊主要有從dq 旋轉坐標系到兩相靜止αβ坐標系的Park-1變換，從兩相靜止αβ 坐標系到dq 旋轉坐標系的Park 變換以及從三相靜止ABC 坐標系到兩相靜止αβ坐標系的Clark 變換其表達式如式(4)～(6)所示。

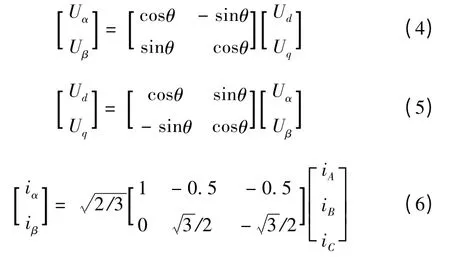
2.3 SVPWM 模塊和逆變模塊

SVPWM 的實現(xiàn)算法在相關文獻［3-5］中已有詳述，本文不再贅述，其建立主要分為幾個步驟:

1)確定空間電壓矢量所在扇區(qū)

各扇區(qū)與Uα、Uβ的關系如式(7)所示:

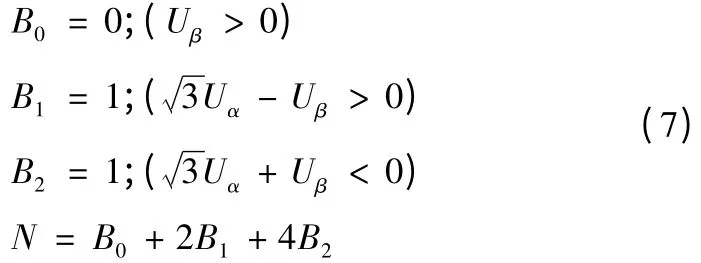
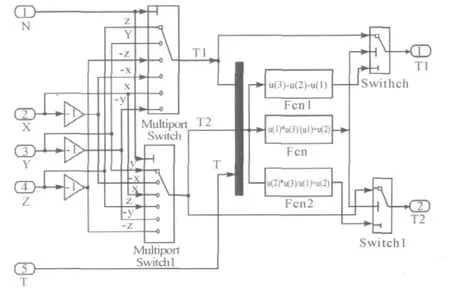
圖5 基本電壓矢量作用時間模塊

得到各扇區(qū)與N 的對應關系，模型如圖3 所示。

圖3 扇區(qū)選擇模塊

2)X、Y、Z 的計算

兩個相鄰電壓空間矢量在一個PWM 周期中的作用時間的公用公式X，Y，Z 的計算如式(7)所示，其模型見圖4。

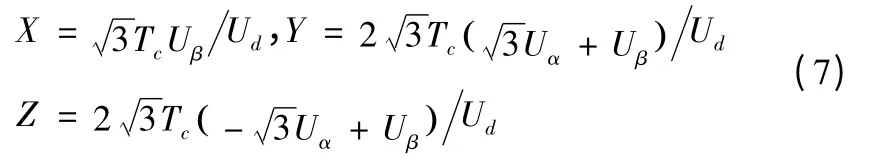
圖4 X、Y、Z 計算模塊

3)基本電壓矢量作用時間模塊

將兩個相鄰的非零電壓空間矢量的作用時間表示為T1，T2，與X、Y、Z 的對應關系如表1。

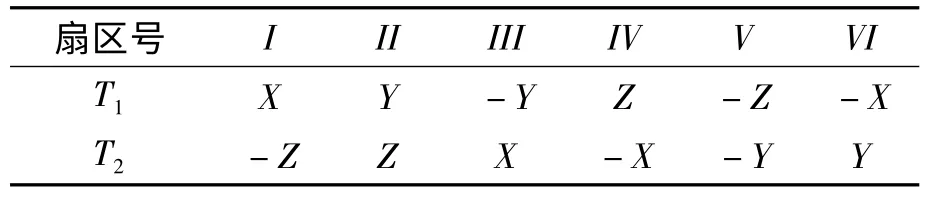
表1 基本電壓矢量作用時間計算公式

之后進行飽和判斷，當T1+T2＞Tc時，

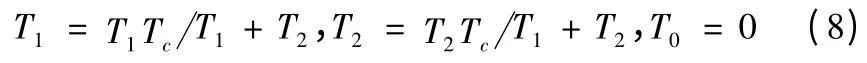
當T1+T2＜Tc時，T1，T2保持不變，

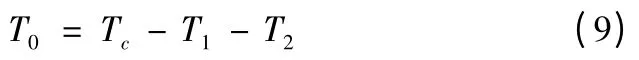
其模型如圖5 所示。

4)Ta，Tb，Tc計算模塊

Ta，Tb，Tc由下式確定:

模型如圖6 所示。

5)PWM 波生成模塊

計算得到的Tcm1，Tcm2，Tcm3值與周期為T，峰值為T/2 的三角波進行比較，可以生成對稱空間矢量PWM 波形。將生成的PWM1，PWM3，PWM5 取反就可以生成PWM2，PWM4，PWM6。其模型如圖7 所示。逆變器模塊由Matlab 自帶的模型生成，直流母線電壓Udc 取230 V。

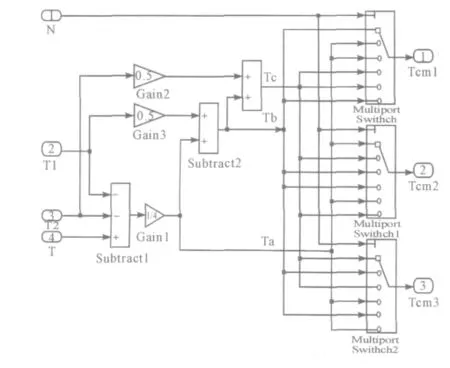
圖6 Ta，Tb，Tc 計算模塊

2.4 電機模型

永磁同步電機模型直接由Matlab 自帶的模型生成，磁通選擇正弦波模式。

2.5 檢測模塊

永檢測模塊也由Matlab 自帶的模型生成，主要由三相電流、轉子角速度、轉子角度、輸出轉矩等組成。

由以上各模塊得到完整的永磁同步電機三閉環(huán)控制系統(tǒng)仿真圖如圖8 所示。

圖7 PWM 波生成模塊

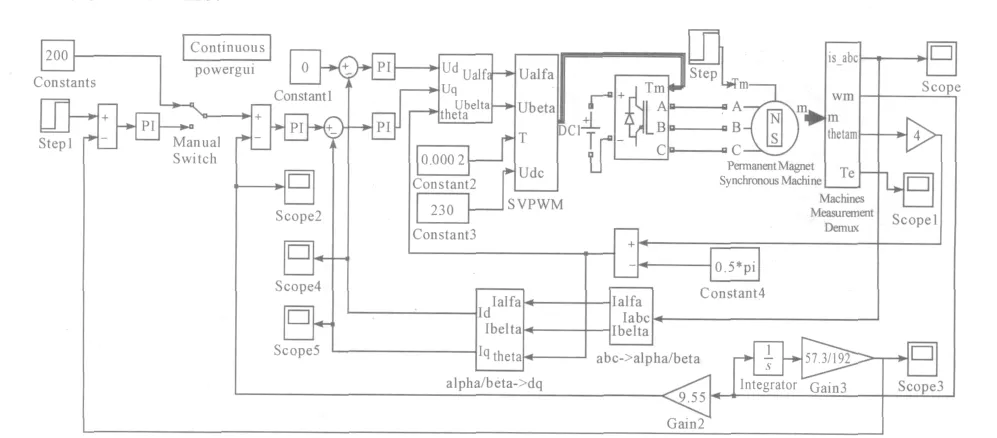
圖8 永磁同步電機空間矢量控制仿真模型

3 仿真結果

為了驗證系統(tǒng)性能及所設計的仿真模型的正確性和有效性，進行了仿真實驗。仿真參數(shù):電機轉動慣量J =2.627 ×10-3kg·m2，定子相電阻R =2.6 Ω，轉子永磁體磁勢Ψf=0.185Wb，等效電感L=5 ×10-3H，極對數(shù)pn=4，粘滯摩擦系數(shù)B=1.43 ×10-4N·m·s，減速器減速比為1∶192。

3.1 速度仿真

仿真條件為電機空載啟動，轉速給定為300 r/min，在t=0.04 s 時突加負載轉矩6 N·m。電機的轉速、轉矩曲線以及定子三相電流如圖9 ～11 所示。

從圖中可以看出，電機在空載啟動時電流、電磁轉矩迅速達到最大值，然后穩(wěn)定在正常值;在0.04 s 突加負載轉矩時，電流、電磁轉矩經(jīng)過一個輕微的振動過程后分別穩(wěn)定在一個新值。轉子角速度迅速穩(wěn)定到給定轉速，存在一定的超調(diào)，突加負載時轉速有所降低，但能迅速恢復到額定狀態(tài)，穩(wěn)態(tài)運行時無靜差。

3.2 位置仿真

仿真條件為電機空載啟動，位置給定為10°，在t =0.5 s時突加負載轉矩10 N·m。位置及轉矩輸出曲線如圖12 ～13 所示。

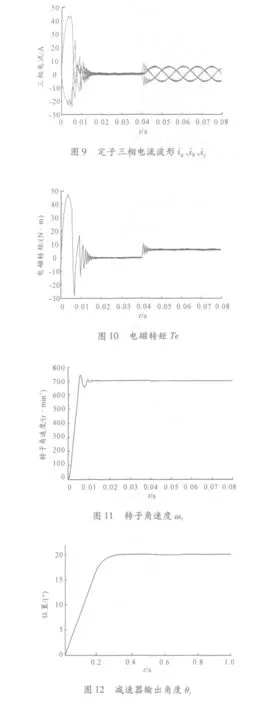
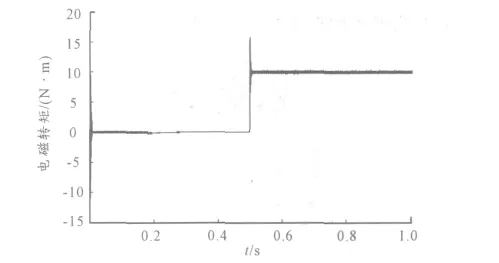
圖13 電磁轉矩Te

從圖中可以看出，位置響應快速、無超調(diào)，突加負載時位置曲線幾乎不受影響，穩(wěn)態(tài)運行無靜差;電磁轉矩在電機啟動和突加負載轉矩時有明顯振蕩，但能在很短的時間穩(wěn)定在常值，且此時的位置及轉矩曲線已非常穩(wěn)定平滑。

4 結束語

本文在分析永磁同步電機矢量控制模型的基礎上，在Matlab/Simulink 環(huán)境下建立了基于空間矢量脈寬調(diào)制控制的永磁同步電機三閉環(huán)伺服系統(tǒng)，采用PI 控制策略設計了系統(tǒng)的電流、速度及位置調(diào)節(jié)器，易于工業(yè)控制的實現(xiàn)。仿真結果表明，系統(tǒng)能平穩(wěn)運行，具有良好的速度響應及位置跟蹤特性，同時為實際電機控制系統(tǒng)的設計及控制研究提供了有效地手段和工具。

［1］Jianguo Zhoua，Youyi Wang. Real time nonlinear adaptive backstepping speed control for a PM synchronous motor［J］.Control Engineering Practice，2005(13):1259-1269.

［2］舒志兵.交流伺服運動控制系統(tǒng)［M］.北京:清華大學出版社，2006.

［3］姚緒梁.現(xiàn)代交流調(diào)速技術［M］.哈爾濱:哈爾濱工程大學出版社，2009.

［4］程曉猛，陸海峰.用于逆變器死區(qū)補償?shù)目臻g矢量脈寬調(diào)制策略［J］.清華大學學報:自然科學版，2008，48(7):1077-1080.

［5］沈艷霞，吳定會.永磁同步電機位置跟蹤控制器及Backstepping 方法建模［J］.系統(tǒng)仿真學報，2005，17(6):1318-1325.

［6］張森，石航飛，陳志錦，等.基于DSP 的永磁同步電機的矢量控制［J］.兵工自動化，2011(10):71-74.