基于遺傳算法的數字羅盤誤差補償方法研究*

鐘 辰，金海紅，任 騰，田 柳

(1.合肥工業大學計算機與信息學院，合肥230009;2.安徽建筑工業學院電子與信息工程學院，合肥230022)

地磁導航是一種重要的導航方式，具有無源、無輻射、全天時、全天候、全地域、能耗低的優良特征，應用前景廣泛［1］。地磁導航可以作為組合導航的輔助導航方式，與GPS及仿生導航等結合起來，可以構成一種有多余度和導航準確度更高的多信息源組合導航系統。地磁羅盤是地磁導航的重要工具。依據地磁的數字羅盤由于其全固態等優點，被當作許多載體測量航向的首選方法［2］。羅盤本身在制造安裝中存在一定的誤差、磁傳感器容易受外界磁場的干擾等因素都將影響磁羅盤在應用中的穩定性和精度。設計合理的磁羅盤系統，對誤差進行分析和補償就顯得很重要。

本文在傾斜補償式數字羅盤硬件基礎上，對羅盤誤差的來源進行了詳細的分析，研究了相應的誤差補償算法，經實驗驗證，可以有效提高羅盤的精度。

1 數字羅盤系統

地磁場是地球的固有資源，在任何情況下地球磁場的方向始終指向磁北，強度約為0.5 Gauss～0.6 Gauss［3］。本文的數字電子羅盤就是在用磁阻傳感器測量磁場強度的三軸分量、用加速度計采集羅盤姿態角信息的基礎上，通過解算求得航向角［4］。

羅盤的軟件設計采用基于Kei1C51編譯器的Windows集成開發環境uVision3，使用單片機C語言來編寫程序。軟件采取模塊化設計，主程序負責整個系統的控制，調用各子程序完成相應的功能;子程序模塊負責完成各自的指定功能，供主程序調用。

2 誤差分析

由于磁阻傳感器本身在制造、安裝過程中會存在一些誤差，并且磁阻電子羅盤易受外界磁場干擾(如電源噪聲、外磁場干擾、周圍鐵質物體等)，羅盤不可避免出現誤差。其誤差主要可分為兩類:系統自身存在的誤差(如制造誤差、安裝誤差)，由于周圍鐵磁環境造成的環境誤差。

系統自身誤差 磁羅盤系統自身的誤差主要有制造誤差和安裝誤差。制造誤差包括三方面:PCB生產工藝以及芯片的安裝，并不能保證傳感器的3軸完全的正交引起的正交誤差;由于傳感器的靈敏度和放大倍數的乘積不相等引起的靈敏度誤差;由于傳感器、模擬電路和AD轉換的零點不為零引起的零位誤差。磁羅盤在安裝時，由于與載體上的X、Y、Z軸不平行產生的誤差稱為安裝誤差。

環境誤差 環境誤差是由磁阻傳感器周圍的鐵磁材料影響而引起的［5］。當羅盤處于沒有任何鐵磁材料的空曠區域內工作時，不會對地球磁場產生任何干擾，但事實上羅盤都被安裝在附近很可能存在鐵質材料的環境里，這些環境里的鐵質材料以及PCB板上各種含有鐵磁性材料的元件都會產生干擾或彎曲地球磁場從而改變羅盤方向的鐵質金屬效應。

這種磁場干擾可以分為硬鐵干擾和軟鐵干擾兩類。硬鐵干擾產生于永久磁鐵或被磁化的金屬，載體上硬鐵包括直流電流、永久磁鐵和電機等，這些干擾與羅盤的相對位置固定，由于每個輸出點都受到固定大小的干擾，相當于在羅盤的輸出值上增加了一個定值，使羅盤輸出曲線圖的圓心被偏移了。硬鐵干擾在較短的工作周期內可認為具有較好的穩定性。軟鐵干擾產生于地球磁場和羅盤附近的任何磁性材料之間的相互作用，干擾程度與軟鐵材料、傾角、激勵磁場以及軟鐵與磁羅盤的相對位置有關，使羅盤輸出曲線圖變成一個橢圓［6］。由于軟鐵干擾可近似認為與外加場大小成比例，因此軟磁影響與航向角有關，相當于在地磁場各分量上疊加一成比例的磁性影響。

綜上，磁羅盤誤差描述公式如下:

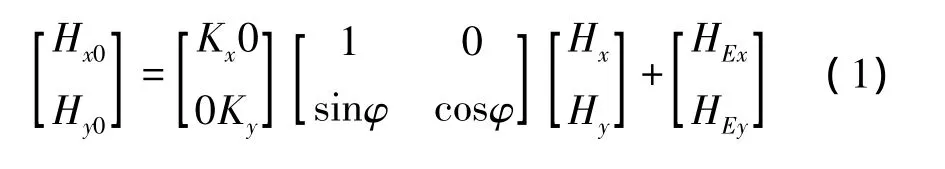
式中，HEx、HEy為硬磁影響系數;kx、ky為軟磁影響系數;φ為非正交誤差影響系數。另外，靈敏度誤差和零位誤差分別相當于軟磁影響矩陣乘以相應的系數和硬磁影響矩陣疊加零點誤差，已經綜合在公式中。

3 誤差補償算法

針對數字羅盤誤差的主要部分，當前有許多算法對誤差進行補償，由于這些算法的原理和側重點不同，對羅盤精度的修正效果也各不相同。

本文實踐了幾種誤差補償算法并做了對比。一種粗略校正鐵磁力的方法是自差粗校正法［7］。這種方法就是簡單地算出磁場干擾導致的偏移量和畸變程度從而進行相應的修正，簡單易行，但是精度不高。在計算羅差補償系數時，用誤差平方和最小原理，即最小二乘法［8］求取，這便是最小二乘誤差補償方法。

綜合各種算法對磁羅盤誤差的補償效果及算法的時間開銷，本文采用基于遺傳算法［9］的誤差補償方法。該算法由于其智能性，尤其適用于處理多參數優化問題，補償效果理想。

根據前述的誤差分析，磁羅盤誤差補償過程即3個誤差矩陣所對應的5個誤差參數HEx、HEy、kx、ky、φ的最優化求解過程［10］。算法流程圖如圖1所示。

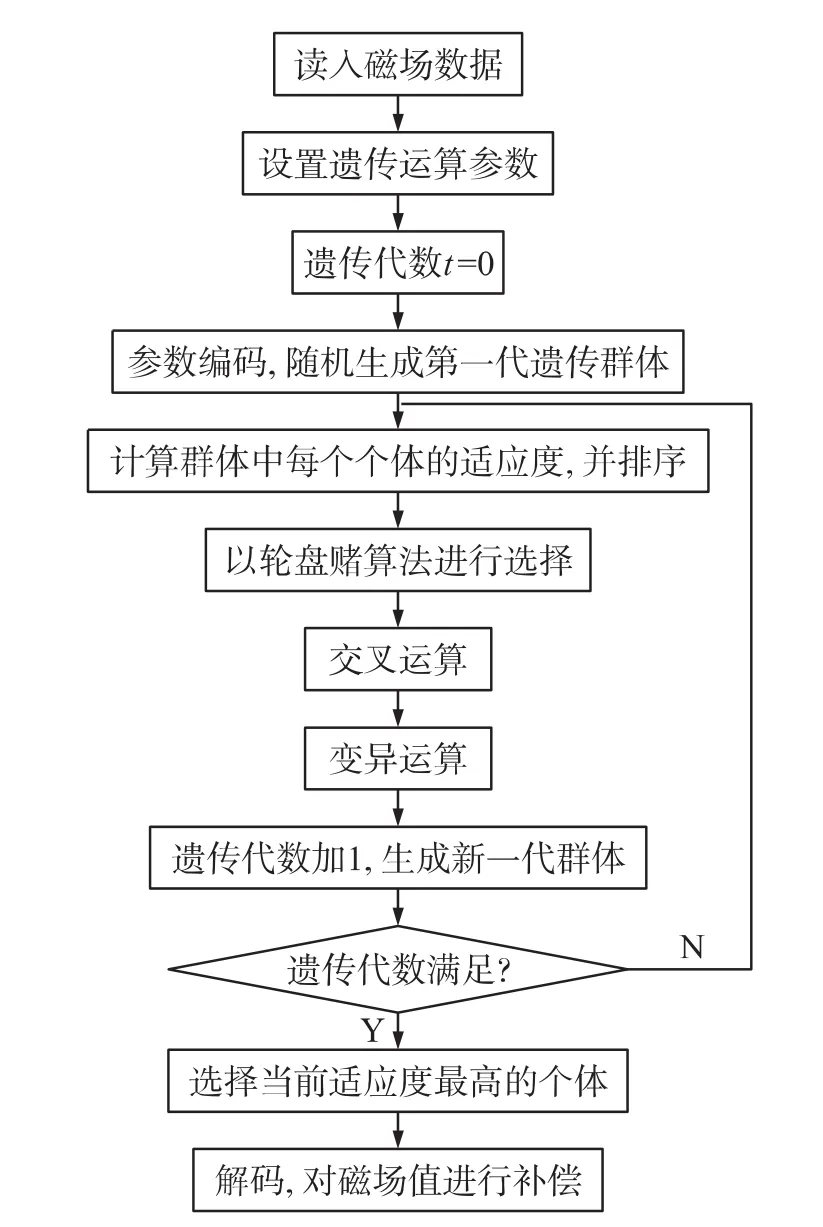
圖1 遺傳算法流程圖

根據遺傳算法原理［11］，其主要步驟包括:

①編碼 編碼是遺傳算法處理的第1步。本文使用基本遺傳算法固定長度的二進制符號串來表示群體中的個體，其等位基因由二值{0，1}所組成。初始種群中各個個體的基因值可用均勻分布的隨機數來生成。本文中需要編碼的參數共有5個:HEx、HEy、kx、ky、φ，共使用 30 bit二進制來編碼。其中，HEx、HEy的取值范圍是［－32768，32768］，kx、ky的取值范圍是［0.6，1，3］，φ 的取值范圍是［－0.083，0083］。

②生成初始種群 種群即是由若干染色體構成的集合。在這里我們隨機選取60個編碼時產生的染色體構成初始種群。

③解碼 解碼就是計算二進制編碼的染色體所對應的十進制數。根據參數取值范圍和其編碼位數，可以根據式(2)計算得到。

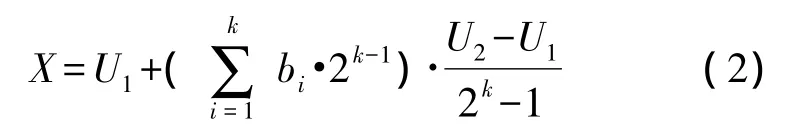
式中，假設某一個體的編碼為 bkbk－1…b2b1，該參數的取值范圍是［U1，U2］。

④確定適應度函數，計算適應度值 適應度函數是為了體現染色體的適應能力而引入的函數［12］。

在不存在誤差時，磁羅盤轉一圈輸出應當是個標準的圓。誤差的影響會使正圓偏移為橢圓，進行誤差校正的理想效果是使橢圓變回正圓。這里適應度函數可以根據磁羅盤轉一圈時，修正后磁場值的方差來確定。考慮到偏移越多，方差越大，遺傳算法保留適應度大的個體，而方差越小的個體越理想，因此選擇方差的相反數作為適應度函數。但遺傳算法適應度函數具有非負性，為此在方差取反的基礎上疊加一個較大的閾值將其變為正數以符合算法的要求。適應度函數f(t)計算公式為:

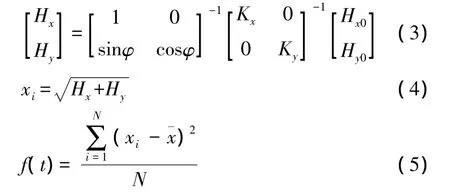
⑤選擇 選擇就是從群體中選擇優勝的個體，淘汰劣質個體。本文使用遺傳算法中經典的輪盤賭算法:首先針對當前種群中的每個染色體算出其對應的適應度函數值，分別記為 f1，f2，f3，…，fM，再算出它們的和fsum，則可得每個解對應的選擇概率:

計算每個染色體的累積概率:

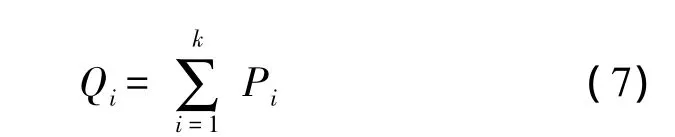
根據輪盤賭選擇算法，產生［0，1］區間均勻分布的隨機數r，若r≥Q1，就選擇染色體Ui，否則選擇第 k 個染色體，使得 Qk－1≤r≤Qk。

⑥交叉 使用單點交叉算子。其運算方法是隨機選擇一個染色體串的節點，然后交換兩個父輩節點右端部分來產生子代。假設交叉概率為25%，即在平均水平上有25%的染色體產生了交叉。

⑦變異 使用基本位變異算子。即如果該位基因是1，則變異之后就變為0。將變異概率設為P=0.02。在確定變異基因時，首先產生［0，1］區間均勻分布的隨機數r，如果第i次得到的r＜P，就對第i個染色體進行變異。

當遺傳的代數滿足要求的時候，就可以根據適應度函數選擇出當前最佳的個體，然后進行解碼，這就得到磁羅盤最佳誤差補償參數。

4 實驗及分析

由于羅盤常被置于不平的載體上，本文使用加速度計測得載體傾角，對羅盤進行傾斜補償［4，7］。傾斜補償可以有效降低羅盤姿態造成的誤差，但是由于環境磁場的干擾，仍舊存在較大誤差，需要相應的算法進行補償。

(1)環境誤差補償實驗

系統軟硬件設計完成之后，對羅盤系統進行了標定和實驗。在0°～360°之間每個10°測量一次航向角數據。并且運用遺傳算法對航向角進行補償，計算其產生的誤差。誤差結果如圖2所示。

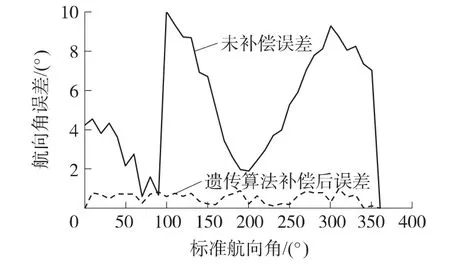
圖2 遺傳算法誤差示意圖

測量數據顯示，在未進行誤差補償時，航向角的平均誤差為10.81°，說明進行誤差補償的必要性。在本系統中，遺傳算法可以有效補償由于環境磁場造成的誤差，可將平均誤差由10.81°降低到0.53°。

(2)不同地點外場對比實驗

在不同地點下開展了外場實驗，分別為:電子干擾較大的實驗室、空曠操場、無干擾室內、普通街道。實驗結果如圖3所示，誤差分析如表1所示。

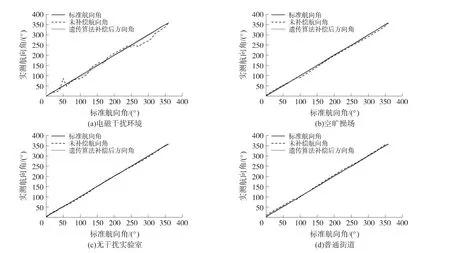
圖3 不同地點外場實驗結果

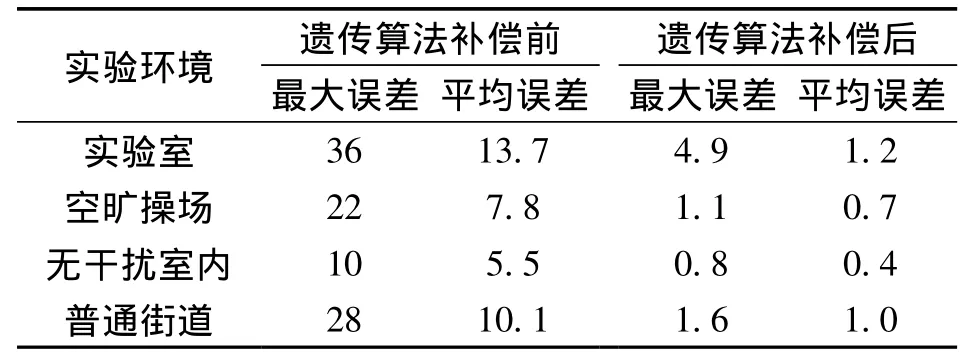
表1 不同測量環境下羅盤系統測量結果 單位:(°)

由結果可見，經過遺傳算法補償之后，多種不同測量環境下本羅盤系統的最大測量誤差不超過5°，可有效實現惡劣電磁環境下的航向角測量。

5 結論

本文在基于磁阻技術的傾斜補償式數字羅盤硬件基礎上，對羅盤誤差來源進行了詳細的分析。提出一種基于遺傳算法的誤差補償方法。

實驗表明，本文所實現的遺傳算法對磁羅盤補償后，在0°～360°范圍內，航向角的測量精度可達±1.6°;在±60°范圍內，羅盤傾角測量誤差不超過±1°，對于60°以外的大傾斜角情況，可以通過等效計算將傾斜角調整到可控范圍內進行補償;惡劣電磁環境下，最大航向角誤差不超過5°。補償后的羅盤可以提供一種精確有效的地磁導航信息。

［1］ 郭才發，胡正東，張士峰.地磁導航綜述［J］.宇航學報，2008，30(4):1314－1319.

［2］ 洪德本.航海儀器［M］.大連:大連海事大學出版社，2003:297－308.

［3］ Honeywell.3-Axis Compass Sensor Set［EB/OL］.www.honeywell－sensor.com.cn，2009－10－16.

［4］ 金海紅，吳東升，田柳，等.傾斜補償式地磁傳感器的設計與誤差補償方法，傳感器與微系統，2010，7(29):33－36.

［5］ 邵婷婷.傾斜補償電子羅盤設計［D］.西安:西北工業大學電子信息學院，2007.

［6］ 杜英，李杰，孔祥雷，等.無航向基準條件下電子羅盤的誤差補償方法研究［J］.傳感技術學報，2010，23(9):1285－1288.

［7］ 沈鵬，徐景碩，高揚.電子磁羅盤測量誤差校正方法研究［J］.儀器儀表學報.2007，28(10):1902－1905.

［8］ Wichman R，Heinonen P，Neuro Y.FIR-Median Hybrid Filters with Excellent Transient Response in Noisy Conditions［J］.Digital Signal Process，1987，38(12):l71－175.

［9］ 王秀.基于遺傳算法的數字磁羅盤誤差補償方法研究［J］.磁性材料及器件，2010，41(4):63－69.

［10］劉建娟，徐曉蘇.遺傳優化模糊神經網絡在組合導航系統中的應用［J］.傳感技術學報，2006，19(6):2630－2633.

［11］ 席裕庚.遺傳算法綜述［J］.控制理論與應用，1993，13(6):697－708.

［12］雷英杰.MATLAB遺傳算法工具箱及應用［M］.西安:西安電子科技大學出版社，2005:1－200.