抗野值魯棒濾波在微慣性組合導航中的應用*

高宗余，方建軍 ，郭文榮

(1.北京聯合大學自動化學院，北京100101;2.北京交通大學電氣工程學院，北京100044)

隨著微電子技術的發展而出現的微電子機械系統MEMS(Micro Electro Mechanical System)器件具有體積小、功耗低、響應快、靈敏度高、成本低的優點，由其構成的一些微慣導系統逐漸的應用于機器人、車載系統及無人機系統中;但是，在其構成的系統狀態估計中，測量數據都會受到噪聲的污染，由于MEMS傳感器的故障、數據傳遞過程中出現的錯誤和環境的干擾，量測序列中不可避免地包含著某些錯誤信息，我們稱之為野值。如果不把野值及時檢測和剔除，將會對微慣導測量過程中誤差狀態的估計產生很大的影響，從而導致系統精度的降低。為此人們提出了許多野值檢測和剔除的方法。

在現有的野值檢測方法中，文獻［1］提出了基于ARMA模型的在線辨識，通過模型參數的變化來判斷是否出現野值，但是這是基于系統的噪聲統計特性穩定和已知的情況;文獻［2－3］中基于濾波新息的統計特性，檢測野值，通過直接剔除觀測值或修正觀測值來去除野值的影響;但是魯棒H∞濾波在應用過程中并不對噪聲統計特性做假設，所以這些方法就不適用。在現有的野值剔除方法中，文獻［4］提出了利用新息平均值代替含野值新息的方法，但是此方法在野值成片出現的情況下效果不佳。

本文采用小波變換檢測信號奇異性的方法，在時頻域對野值進行處理。通過分析最細尺度上的系數信息，快速檢測出野值點，之后采用基于信息擴散原理的新息修正魯棒H∞濾波方法，通過對車載MEMS-INS/GPS組合導航的仿真表明，該算法能有效去除野值的影響，大大提高了野值條件下狀態估計的精度。

1 野值對魯棒H∞濾波的影響

對于線性動態量測系統

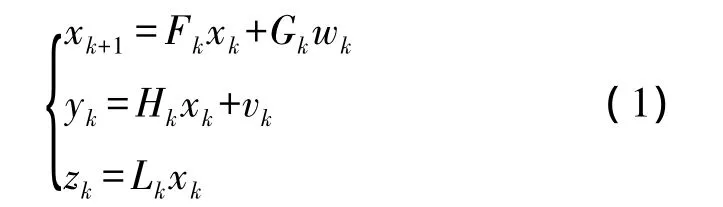
魯棒 H∞濾波算法［5］如下:

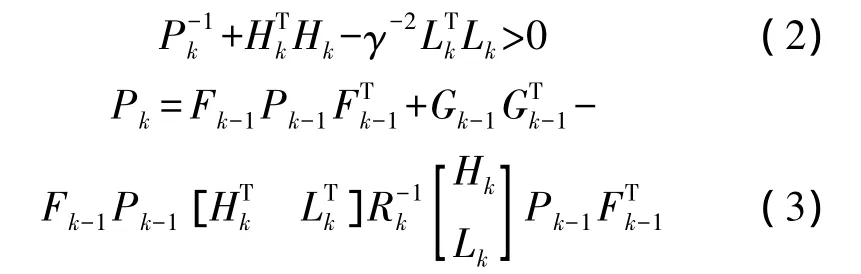
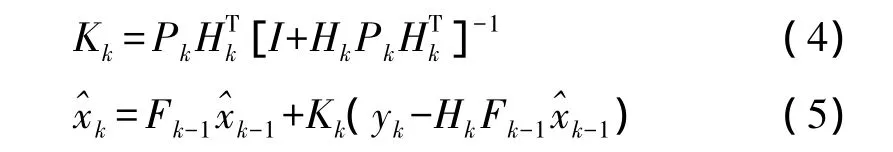
魯棒 H∞濾波中，量測估計誤差 ek=yk－HkFk－1^xk－1被稱為新息，新息反映了當前量測帶來的新信息，由濾波方程可以看出，狀態估計值等于預測值和新息的加權和，而權重與量測自身無關，只與量測精度和預測精度有關，新的量測數據所帶來的新息以線性組合的方式對魯棒H∞濾波估計產生影響，所以在濾波過程中量測序列含有野值時，將會對濾波估計產生很大的影響，由于異常的量測數據都會在新息中體現出來，因此可以通過判斷新息特性來判斷量測值中是否含有野值，通過修正新息來剔除野值。

2 野值檢測

2.1 基于小波變換的野值點檢測

Matllar提出了一種使用小波變換模的極大值降噪的方法;Donoho提出在小波意義上，規則信號的絕大多數能量都集中在同一尺度上的少數的小波系數上，而噪聲是分散開來的。因此，我們從野值的小波變換系數入手檢測野值。

ψ(t)為一小波基函數，尺度因子和平移因子分別為a和b，信號f(t)小波變換定義為:

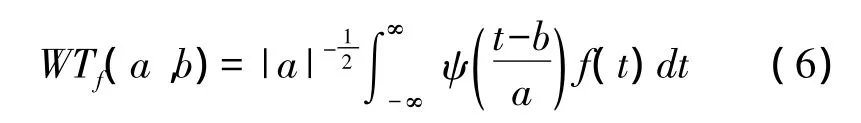
小波變化將信號在t～ω域中展開，最細尺度對應著小波變換的最高頻率，信號的小波變換，在最細的尺度上小波變換系數主要由噪聲和野值的小波變換系數構成，野值在時域具有較大的幅值;由于變換的線性特征，其小波系數表現為獨立的極值，在頻率上比噪聲更持久集中。而噪聲的小波系數幅值很小，因此，野值的探測通過門限τ尋找最高頻上的系數來檢測。

影響細尺度上小波系數的幅度是小波函數ψ(t)的消失矩階數，在所有的正交小波中，Haar小波僅有一階消失矩。它的支集長度為［0，1］，在所有的小波中也是最小的支集長度，支集包含有奇點的Haar小波產生大幅值的小波變換系數。因此它不太適合逼近光滑的函數，對階躍信號不敏感，對野值很敏感，會產生大幅值的系數。Haar小波對獨立的野值點響應很強烈，階躍信號幾乎都被壓制，這就是采用Haar小波檢測野值的原因。本文從時頻域，采用Haar小波對野值進行檢測，下邊對其步驟進行描述:

(1)小波分解 設{VJ}J∈Z是一個給定的多分辨率逼近，φ和ψ分別為相應的尺度函數和小波函數。當 J→∞時，VJ充分逼近 L2，假定要分析的信號為 f(t)，f(t)∈VJ1(J1∈Z)，則信號 f(t)可以正交分解為:，其中＜，＞表示內積，高頻部分fdJ是信號f(t)在尺度J1上的近似估計。

對于在尺度J2上的觀測序列x(n)∈l2(z)

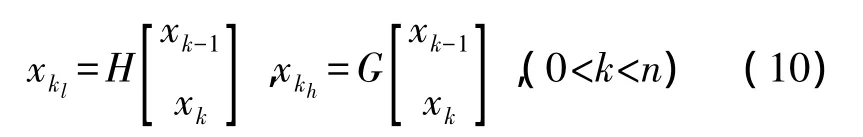
其中:xkl觀測序列在低一級分辨率(J2+1)上的近似估計，xkh是相應的細節，它們還分別代表著觀測序列的位置信息和速度信息。

(2)野值檢測 由于野值的存在，xkh和xkl中包含很多野值的信息。野值信息大大降低了濾波性能，甚至會發散，因為最細尺度上的小波變換系數主要由野值和噪聲組成。

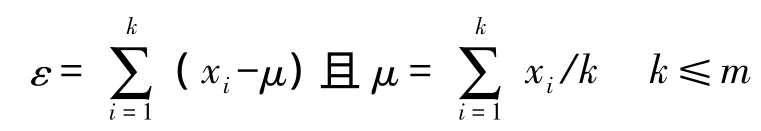
3 野值剔除

3.1 信息擴散［6-7］

設 W={w1，w2，…，wn}是知識樣本，L 是基礎論域，wi的觀測值為 li，設 x=φ(l－li)，則當 W 非完備時，存在函數λ(x)，使li點獲得的量值為1的信息可按λ(x)的量值擴散到l上去，擴散所得的原始信息分布為:

式(11)能很好的反映W在總體的規律，這一原理稱為信息擴散原理。

根據這一原理對母體概率密度函數的估計稱為擴散估計，設λ(x)為定義在(－∞，+∞)上的一個波雷爾可測函數，Δn＞0，為常數，則

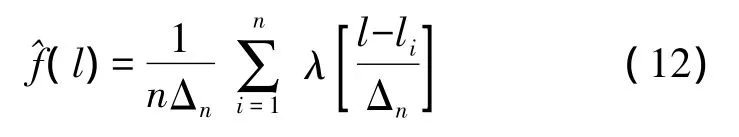
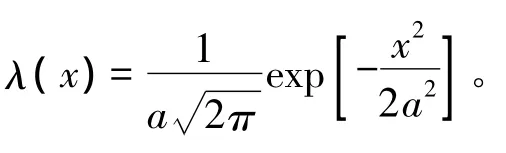
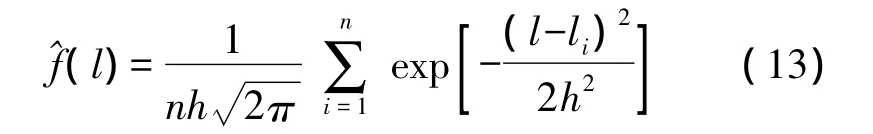
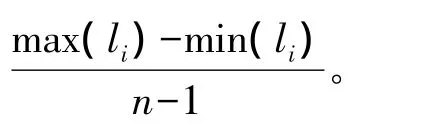
3.2 新息修正

本文采用信息擴散法對量測值所產生的新息進行修正，具體步驟如下:

(1)設各個狀態估計的新息序列為{l1l2…

ln}，假設第一個狀態估計的新息l1出現野值，利用上節給出的小波系數變換方法進行野值檢測。

(3)利用替代方法得出新的新息，在此過程中，本文摒棄了含有野值的新息l1，取而代之是正常的新息，即其它狀態估計的新息{l2… ln}的加權和，權值則是由正常新息密度函數^f(li)，i=2，…，n與含野值新息的密度函數(l1)之比得出的，替代新息的表達式為

基于信息擴散原理的新息修正法充分利用了正常的新息，通過自適應比例加權的方式對含有野值的新息進行替代，從而達到保障了濾波的精度的目的。

4 仿真

采用基于MEMS的SINS/GPS組合導航的車載系統［8］，實驗裝置基本構造為一個三軸陀螺ADISI16355，包含三軸正交陀螺及三軸加速度計以及溫度補償電路，此外附加GPS測試版。系統初始位置為(40°N，118°E)，系統以 5 m/s2加速度運行。標準運動軌跡如圖1所示。

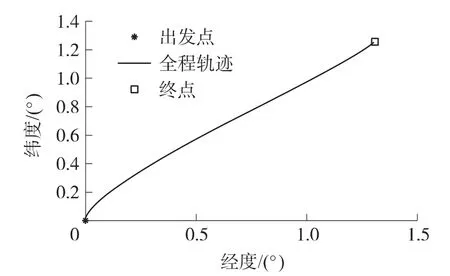
圖1 系統運動軌跡

微慣導組合系統狀態向量x=［δL δλ δh δVEδVNδVUφEφNφUtu˙tru］，其中 tu為GPS時鐘誤差引起的等效距離誤差，˙tru為GPS時鐘誤差引起的等效速度誤差，量測偽距z1=［Δρ1Δρ2

Δρ3Δρ4］，偽距率z2=［Δ˙ρ1Δ˙ρ2Δ˙ρ3Δ˙ρ4］。Δρi為第i顆衛星到車載體的偽距，Δ˙ρi為第i顆衛星到車載體的偽距率。給定仿真條件:狀態矢量x的初值為0，陀螺常值漂移為5°/h，隨機漂移白噪聲為3°/h，一階馬爾科夫噪聲相關時間為3 600 s，驅動噪聲為 1.5°/h。加速度計常值漂移為 0.05 gn，隨機漂移白噪聲為 0.02 gn，一階馬爾科夫噪聲相關時間為7 200 s，驅動噪聲為0.005 gn。GPS偽距誤差白噪聲為(12 m，12 m，15 m)，偽距率誤差白噪聲為(0.2 m/s，0.2 m/s，0.3 m/s)。時鐘誤差白噪聲為(2 m，2 m，2 m)，時鐘頻率誤差一階馬爾科夫噪聲相關時間為500 s，驅動噪聲為0.05 m/s。γ為2.1。微慣導組合系統狀態方程和量測方程的矩陣參數具體表達形式本文不做累述，參看文獻［9－12］。

假設t=30 s時量測偽距的第一個分量出現野值，設含野值的新息值為100，新息數據如圖2所示。

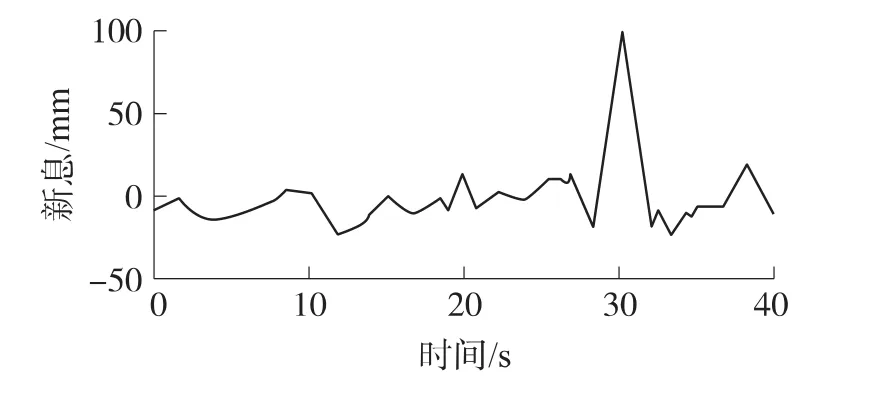
圖2 含單個野值的新息

首先進行野值檢測，對10 s～30 s的數據進行分析，首先取 a=0.1，則 k=2.98，10 s～30s的數據均值為4.52，標準方差為22.40，野值檢測門限為(－36.28，48.43)，可知，新息在 t=30 s為 100，超出此范圍，暫時認定為野值點。然后取 a=0.05，k=4.12，10 s～29 s的數據均值為 0.52，標準方差為11.86，野值檢測門限為(－28.84，41.12)，可知新息在t=30 s為100超出此范圍，認定為野值。

然后進行野值剔除，本文分別對兩種種新息修正方法進行比較，第1種為增益矩陣修正法，對濾波過程中與含野值的新息對應的那一行的K值人為置零。第2種為本文提出的新方法，當第1顆衛星偽距含有野值時，充分利用第2到4顆衛星偽距的正確性，基于信息擴散原理利用正確新息的加權和代替含野值新息。

當檢測出t=30 s有野值時，對第1種方法進行仿真。如圖3和4所示。

圖3 含單個野值的緯度濾波估計

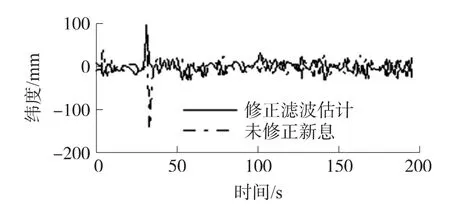
圖4 含單個野值的經度濾波估計

由仿真結果可以看出，由于組合導航量測值之間是耦合的，只是單純的人為置零某一行增益矩陣并不能消除野值對其它狀態估計所產生的影響。

然后利用本文提出的方法在單個野值出現的情況下進行仿真，如圖5和6所示，在成片野值出現的情況下進行仿真，如圖7所示。

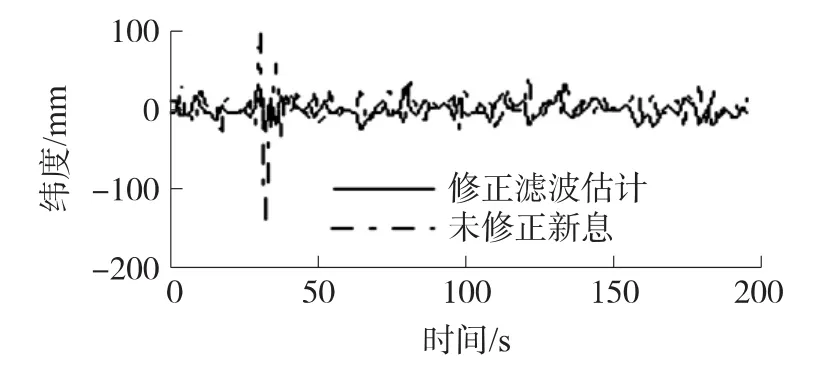
圖5 含單個野值的緯度濾波估計

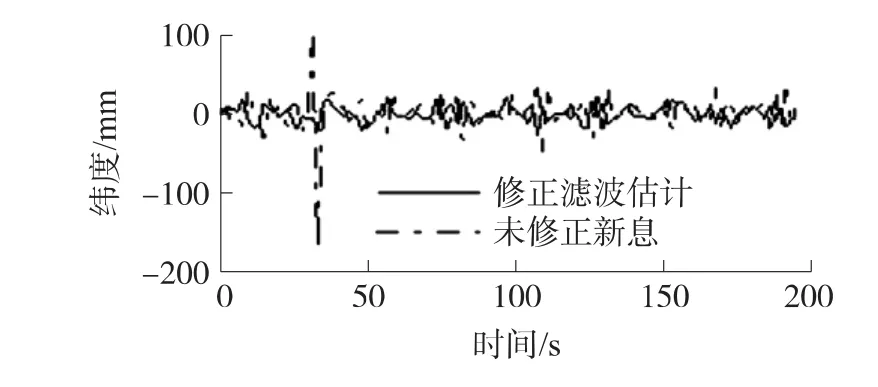
圖6 含單個野值的經度濾波估計

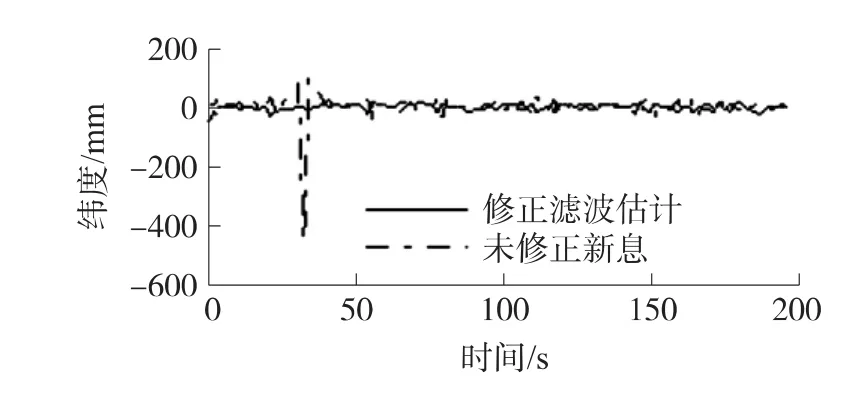
圖7 含成片野值的緯度濾波估計

由仿真結果可以看出，無論是單個還是成片野值，基于擴散原理的新息修正方法都能夠充分利用正常新息，從而達到消除野值的目的。

5 結論

實際過程中，量測值中出現野值的現象是經常發生的，如果不及時處理，會導致濾波精度下降。本文提出的采用小波變換系數特性，通過最細尺度上的小波系數來檢測野值點。然后采用基于信息擴散原理的新息修正法，可在線自適應調整新息，消除野值對濾波的影響，特別對成片野值的出現有很好的魯棒性，通過微慣性車載系統SINS/GPS組合導航的仿真可得出，新算法既保證了野值檢測的準確性，又保證了濾波的精度，具有良好的應用價值。

［1］ 顏東，張洪鉞.基于辨識ARMA模型的野值剔除方法與卡爾曼濾波修正算法［J］.信息與控制，1995，24(3):183－187.

［2］ 祝轉民，秋宏興，李濟生.動態測量數據野值的辨識與剔除［J］.系統工程與電子技術，2004，26(2):147－150.

［3］ 柳海峰，姚郁，盧迪.Kalman濾波新息正交性抗野值法研究［J］.電機與控制學報，2003，7(1):40－43.

［4］ 羅志斌，劉先省，胡振濤等.基于新息特性抗野值Kalman預測算法［J］.河南大學學報，2006，6(4):79－82.

［5］ 付夢印，鄧志紅，張繼偉.Kalman濾波理論及其在導航系統中的應用［M］.北京:科學出版社，2003.

［6］ 黃崇福，王家鼎等.模糊信息優化處理技術及其應用［M］.北京:北京航空航天大學出版社，1995.

［7］ 盧崢，張帆，程京.基于信息擴散的Kalman濾波抗野值研究［J］.科學技術與工程，2007，8(7):1525－1528.

［8］ 高宗余，李德勝，王躍宗.基于ZUPT的車載MEMS慣性系統的混合濾波［J］.電機與控制學報，2010，14(2):31－35.

［9］ 楊春鈞，袁信.差分GPS偽距與慣導組合技術仿真研究［J］.航天控制，1998，1:62－68.

［10］苑艷華，李四海，南江.基于卡爾曼濾波器的航姿系統測姿算法研究［J］.傳感技術學報，2011:24(12):1723－1727.

［11］張品秀，黃操軍，喬相偉.基于自適應擴展 kalman濾波的SINS/GPS深組合研究［J］.傳感技術學報，2010:23(3):408－412.

［12］徐本連，董學平，王執銓.雙基陣純方位目標跟蹤的抗野值算法研究［J］.東南大學學報，2004:34(增刊)199－203.