計及風速擾動的含風電場電力系統相關性分析研究
孫 琦,尤紅麗,辛 鵬,王斯琦
(1.東北電力大學電氣工程學院,吉林吉林132012;2.吉林省電力有限公司吉林供電公司,吉林吉林132012)
0 引言
隨著風電所占比例增加,對系統穩定性的影響越來越大。波動性和季節性的新能源發電的風電[1-2],在帶來大量綠色可再生能源的同時,也可能將電網帶入一個擾動更頻繁、擾動量更大、非平穩性和隨機性更強的環境中。在這樣的環境中,如何合理的計及風電接入對系統的影響對電網安全運行具有重要意義。文獻[3-5]提出了利用相關分析理論進行故障選相。文獻[6]提出了基于相關分析的暫態差動保護原理。文獻[7]將其應用到中長期電力負荷綜合預測中。文獻[8]對新能源發電功率與電壓偏差進行了相關性分析。文獻[9]在風電場隨機潮流計算中計及了有功無功相關性。但是,目前,估計電力系統信息關聯程度的分析方法仍然很少,特別是考慮風電接入系統后對系統關聯程度及其影響的幾乎未見涉及。因此,本文提出了一種快速估計風電接入系統系統相關程度的新方法。它采用相關分析法快速估計各發電機有功功率,并基于不同風速情況,對系統相關程度作出評價,綜合分析風電接入對系統的影響。
1 永磁直驅風電機組的數學模型
永磁直驅風電機組(Permanent Magnet Synchronous Generators,PMSG)的基本結構如圖1所示。
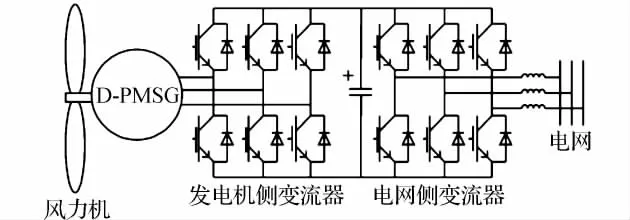
圖1 PMSG風力發電機組示意圖
1.1 風力機數學模型
風力機基本原理是利用風輪接收風能,將其轉換為機械能,通過風輪軸輸送出去。由空氣動力學原理可知,風力機的輸出功率Pm滿足[10,11]:
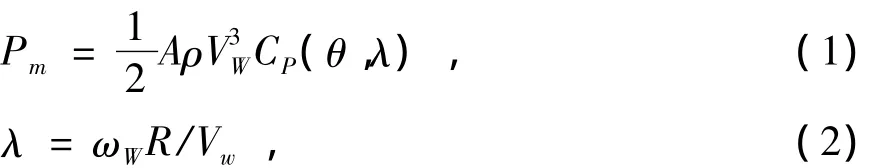
式中:A為槳葉掃風面積;θ為槳距角;ρ為空氣密度;λ為葉尖速比;Vw為風速;ωw為風力機轉子轉速;R為風力機轉子半徑;Cp為與θ和λ有關的功率系數。
風力機從風中捕獲的功率滿足:

則風力機的機械輸出轉矩Tw可表示為
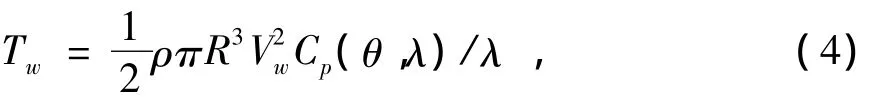
風電機組軸系統模型為
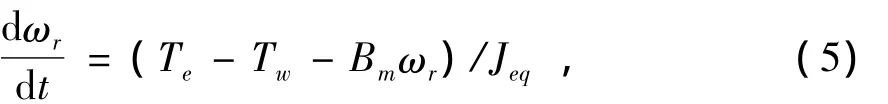
式中:ωr為發電機轉子轉速;Bm為等效轉動慣量; Te為電磁轉矩;Jeq為轉動粘滯系數。
1.2 PMSG數學模型
根據轉子磁場定向得到同步旋轉坐標系下的PMSG的定子電壓方程為[12]
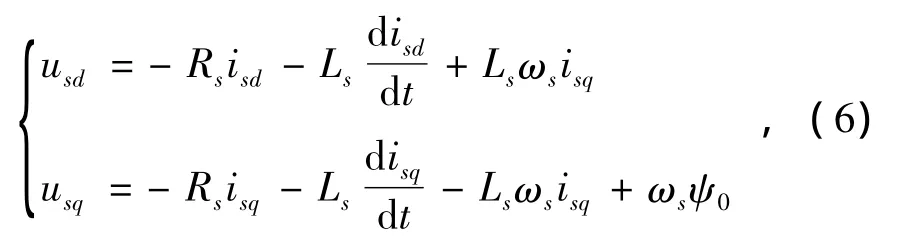
式中:isd、isq和usd、usq分別為永磁同步發電機定子輸出電流、電壓的d軸和q軸分量;Rs和Ls分別為發電機的定子電阻和電感;ωs為同步電角速度;ψ0為永磁體的磁鏈。
電磁轉矩的表達式為
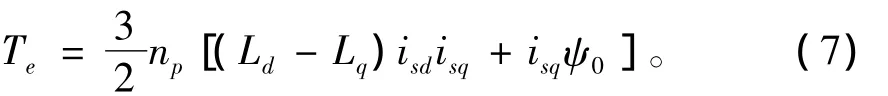
PMSG的永磁體多采用徑向表面式分布,即Ld=Lq,此時發電機的電磁轉矩可簡化為

式中,np為發電機的極對數。
由于發電機的電磁轉矩與定子q軸電流成正比,因此通過調節isq即可調節永磁同步發電機的電磁轉矩,進而調節發電機和風力機的轉速,使之隨風速變化,運行于最佳葉尖速比狀態。
2 相關性、相關分析和相關系數
相關性是指信號的相似和關聯程度。相關分析不僅可用于確定信號,可用于簡單而且對噪聲有抑制能力的信號,所以相關分析在機械振動分析、微弱信號檢測中有一定應用。相關性常用相關系數或相關函數來描述[13]。
對于隨機信號而言,變量x和y之間的相關程度可以用相關系數cxy表示,即
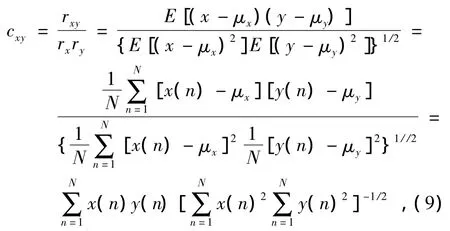
式中:n為離散點編號;N為離散點總數;rxy為變量x、y的協方差;rx、ry為變量x、y的標準差;μx、μy為變量x、y的數學期望(x、y為離散隨機信號時)或均值(x、y為連續信號時),即

在信號處理中,有時會將μx、μy從式(9)中略去。當x、y為同一信號時,一般稱自相關系數,不稱為互相關系數。
本文相關系數使用說明如下:
1)相關系數沒有單位,其值為-1≤cxy≤1。cxy值為1或接近1表示正相關,可判為同相,即兩功率信號同調;cxy值為-1或接近-1表示負相關,可判為反相,即兩功率信號相互振蕩;cxy值為0或接近0表示不相關。
2)cxy絕對值反映兩變量間相關關系的密切程度,絕對值越大說明相關性越強,cxy絕對值等于1為完全相關,cxy=0為零相關。
3 風速模型
由于風力發電機組的輸出功率隨著風速變化而變化,因此,電網將持續受到風電場功率擾動源的干擾。風速的持續變化在一定時間和空間范圍內是隨機的,但從總的、長期統計結果來看,風速的變化仍然具有一定規律。風速變化原則上可由基本風、漸變風、陣風、隨機風組成[14-15]。
3.1 基本風
基本風在風力機正常運行中一直存在,它決定了風力發電機向系統輸送額定功率的大小,反映了風電場平均風速的變化。它可以由風電場測風所得的威布爾(Weibull)分布參數近似確定:
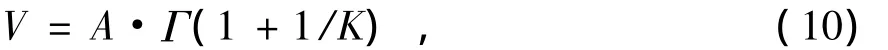
3.2 陣風
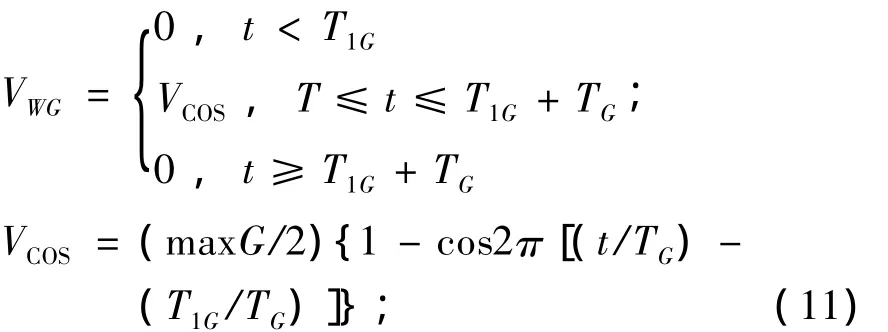
式中,VWG、T1G、TG、maxG為陣風風速、啟動時間、周期和最大值。
3.3 漸變風
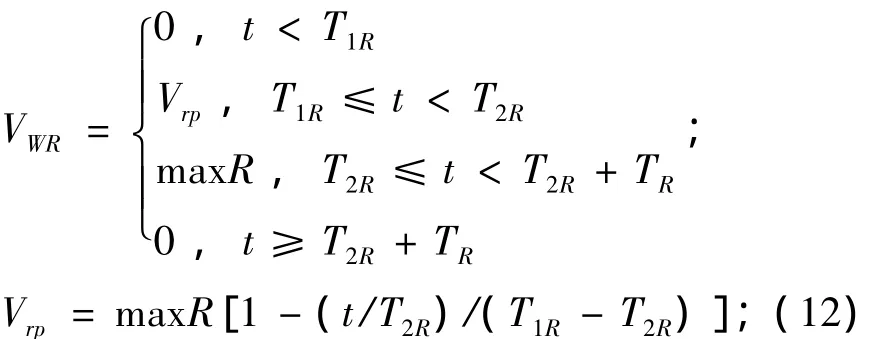
式中:VWR為漸變風速,m/s;maxR為最大值,m/s; TR為保持時間,s;T1R為起始時間,s;T2R為終止時間,s。
3.4 隨機風
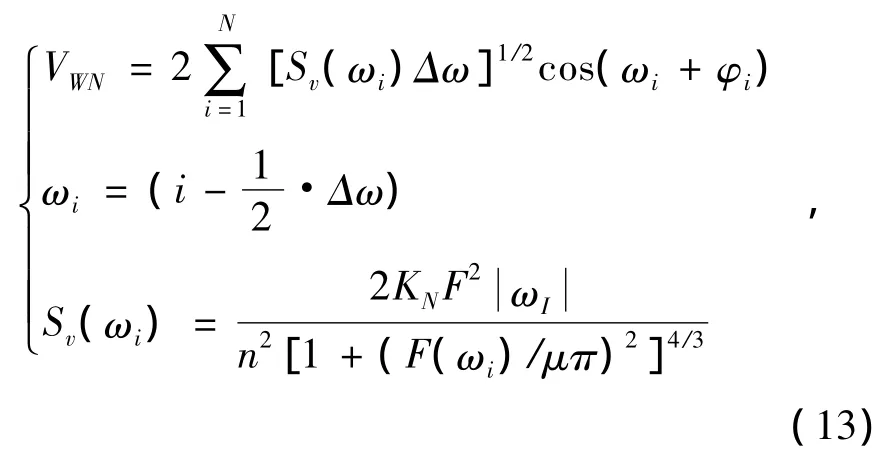
式中:φi為0~2π之間均勻分布的隨機變量;KN為地表粗糙系數(一般可取0.004);F為擾動范圍,m2;μ為相對高度的平均風速。
綜上,風力機風速可表示為
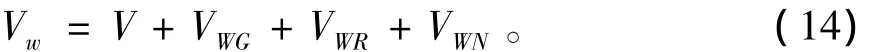
4 仿真研究
4.1 簡單系統
圖2是一個改進的IEEE 3機9節點系統[13],其中一個區為無源負荷中心區。各發電機采用詳細模型、計及勵磁模型,負荷考慮恒阻抗特性。
4.2 不同風速情況下系統的相關性
4.2.1 含噪聲風速情況
0.1 s時在G2上施加幅值標幺值為0.1的階躍擾動。分別記錄系統不加入風機和加入風機1~6 s的2種情況下所有發電機功率信號,這些信號經過相關性理論求取、計算,其相關系數如表1、表2所示。
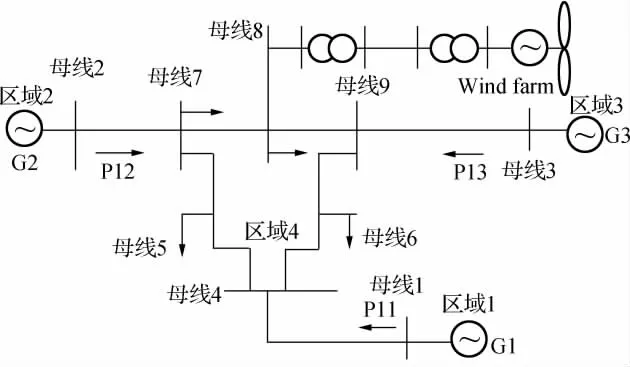
圖2 改進的3機9節點系統示意圖
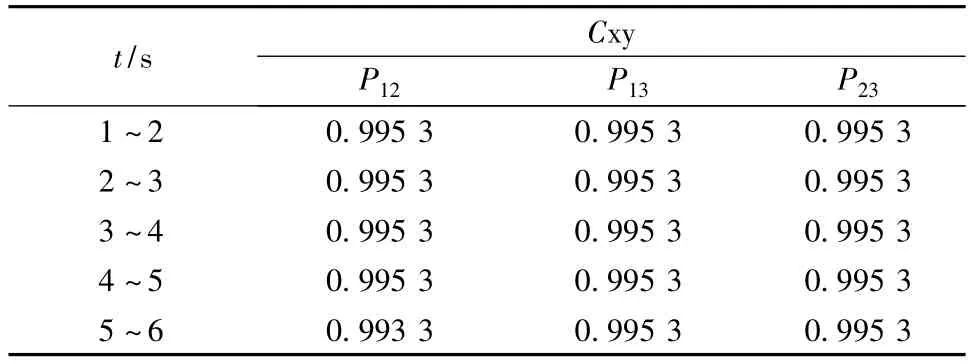
表1 不含風電的有功功率的相關系數
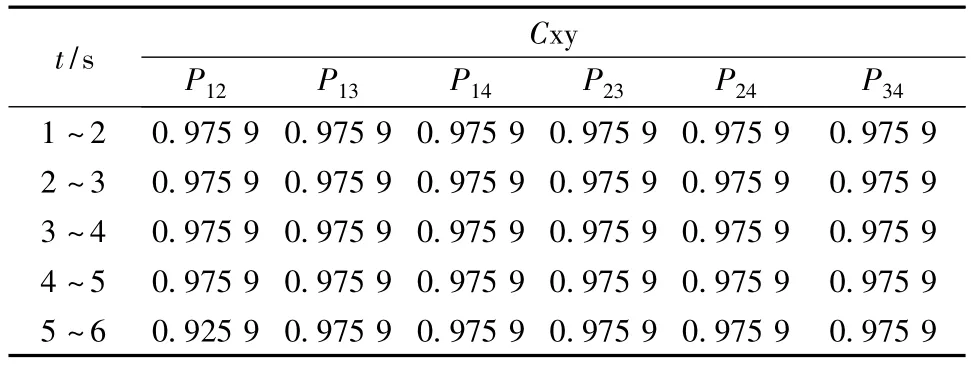
表2 含風電的有功功率的相關系數
由表1~表2可以看出,當在原系統中加入風機后,各個機組之間的相關程度被減弱了,可見風機的接入對系統造成了一定的影響。
4.2.2 含陣風情況
在風速為0~2 s幅值為5的陣風風速下的各發電機有功功率相關系數如表3所示。
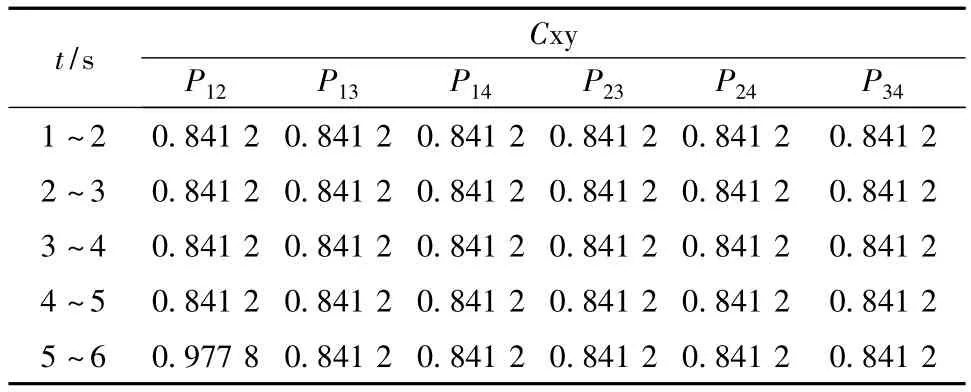
表3 陣風時含風電系統有功功率的相關系數
由表3可以看出當在原系統中加入風機后各個機組之間的相關程度被減弱了。相比于噪聲風速其影響更為嚴重。
4.2.3 含漸變風速情況
在風速為漸變風速下的各發電機有功功率相關系數如表4所示。
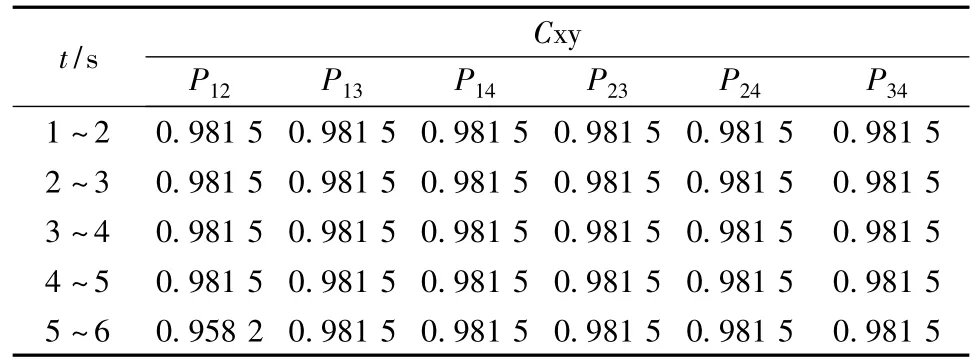
表4 漸變風時含風電系統有功功率的相關系數
由表4可看出當在原系統中加入風機后各個機組之間的相關程度被減弱了。但相比于其它風速其影響較為輕微。
4.2.4 含恒定風速情況
在風速為12 m/s恒定風速下的各發電機有功功率相關系數如表5所示。
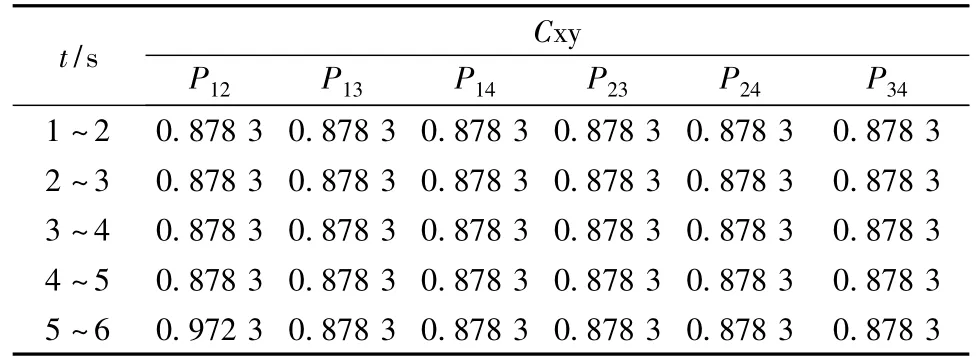
表5 恒風速時含風電系統有功功率的相關系數
由表5可以看出,當在原系統中加入風機后,各個機組之間的相關程度也被減弱了,其影響較為嚴重。
4.3 風機接入不同地點對系統相關性的影響
0.1 s時在G2上施加幅值標幺值為0.1的階躍擾動。分別記錄風機接入不同地點即系統母線4、5、6、7、8、9時的情況。將記錄的1~6 s的風機接入不同地點情況下所有發電機功率信號。經過相關性理論求取,計算它們之間的相關系數如表6所示。由表6可見,互相關系數Cxy清楚地表明了各發電機之間的相關性。
由表6可以看出,當在不同地點接入風機后,各個機組之間的相關程度不同,其對系統影響大小不同,當接入到母線5時,其影響較為嚴重,說明在母線5接入風機對系統影響較大且較惡劣。而在母線9接入時則相關系數比較大,說明風機在此處接入時對系統影響較小。
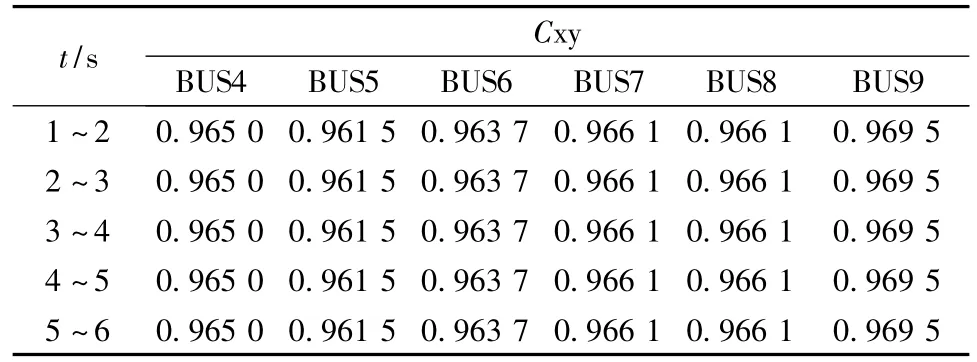
表6 風電接入不同地點的P24有功功率的相關系數
4.4 多個風場不同地點接入對系統相關性的影響
0.1 s時在G2上施加幅值標幺值為0.1的階躍擾動。將容量相同的3個風場分別同時接入系統母線4、7、8,分別記錄風機接入系統母線4、7、8時的情況。將記錄的1~6 s的風機接入不同地點情況下所有發電機功率信號。經過相關性理論求取,計算它們之間的相關系數為0.998 7。可見,當多個風電場不同地點同時接入時對系統的相關程度影響較小,系統的相關程度較強,所以相關系數Cxy清楚地表明了各發電機之間的相關性。
5 結論
本文帶著提高準確性的思考,從含風電接入的角度出發,提出了一種基于相關分析法快速估計含風電系統關聯程度的方法。通過不同類型的風速模型的仿真算例對比,可以看出接入風機之后系統的關聯程度被減弱了,不同風速類型對系統的影響不一致,而且風機接入不同地點對系統影響大小也不同。
[1] 張衛紅,于吉慶,王坤.新能源發電并網標準比較[J].黑龍江電力,2011,33(6):403-408.
[2] ROSS M.Wind Generation presents interconnection challenges[J].North American Windpower,February,2006:55-58.
[3] 王興國,張舉.基于相關分析和模糊推理的故障選相元件[J].電網技術,2006,30(14):93-97.
[4] 李偉,畢天姝,楊奇遜.基于相關分析的同桿雙回線突變量選相新方法[J].電力系統自動化,2011,35(8):58-62.
[5] 成敬周,張舉,陳琛,等.基于高頻暫態分量進行相關分析及模糊推理的選相新方法[J].電力系統自動化,2005,29(5):50-55.
[6] 李巖,陳德樹,袁榮湘,等.基于相關分析的暫態差動保護原理改進及仿真研究[J].繼電器,2003,31(2):64-68.
[7] 虞瑄,程浩忠,王旭,等.基于相關分析的中長期電力負荷綜合預測方法[J].繼電器,2005,33(15):49-52.
[8] 徐群,陶順,肖湘寧,等.新能源發電功率與電壓偏差的相關性研究[J].電測與儀表,2011,48(6):1-5.
[9] 盧繼平,丁然.計及風電場有功無功相關性的隨機潮流計算[J].微計算機信息,2010,26(31):159-161,158.
[10]馬威,包廣清.永磁直驅風電機組的建模與仿真[J].工礦自動化,2010,36(8):49-53.
[11]尹明,李庚銀,張建成,等.直驅式永磁同步風力發電機組建模及其控制策略[J].電網技術,2007,31(15):61-65.
[12]嚴干貴,魏治成,穆鋼,等.直驅永磁同步風電機組的動態建模與運行控制[J].電力系統及其自動化學報,2009,21(6):34-39.
[13]韓松,徐政,武誠.利用相關分析的區間振蕩振型快速估計方法[J].高電壓技術,2011,37(2):436-443.
[14]趙書強,范偉.由風力發電引起的電力系統強迫功率振蕩[J].華東電力,2009,37(1):98-102.
[15]李東東,陳陳.風力發電系統動態仿真的風速模型[J].中國電機工程學報,2005,25(21):44-47.

