基于輸出函數的滑模勵磁控制器研究

張耀天，馬 偉，艾呂澤，李 放

(1．成都電業局，四川 成都610001;2．邢臺電業局，河北 邢臺054001;3．東北電力大學電氣工程學院，吉林 吉林132012)

0 引言

勵磁控制系統對電力系統的小干擾穩定性和暫態穩定性起著至關重要的作用，所以，精確線性化、H∞魯棒控制、變結構控制等非線性控制方法和智能控制方法在電力系統中的勵磁控制中得到了充分應用［1－8］。文獻［9］使用逆推的方法逐步構造李雅普諾夫函數來保證系統的正定性，最后使用反饋線性化得到控制規律，仿真結果證實了該方法的有效性。文獻［10］使用Terminal滑模方法設計了勵磁控制器，能夠估計擾動的上下界，使設計的控制器具有一定的魯棒性。文獻［11］采用反推逐步求解的方法，逐步構造出滑模超平面，通過逐步構造Lyapunov函數，設計了一種魯棒勵磁控制器。但上述這些方法設計的控制器形式比較復雜，因此，本文提出選取輸出函數的輸出變量組成滑模面，通過對其求導得到滑模面為狀態變量的狀態方程，構造李雅普諾夫函數來保證整個系統的穩定性，對含有勵磁電壓的狀態方程進行反饋線性化。使設計的控制器更加簡單實用。

1 數學模型

本文采用的三階發電機模型表達式為

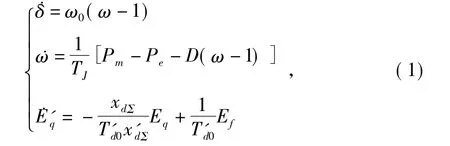
機端電壓Ut的狀態方程為

式中:機端電壓的d軸分量Ud=xqIq;機端電壓的q軸分量 Uq=E′q－ x′dId。

式(1)可寫成如下的形式:

考慮系統的輸出變量，系統可擴展為

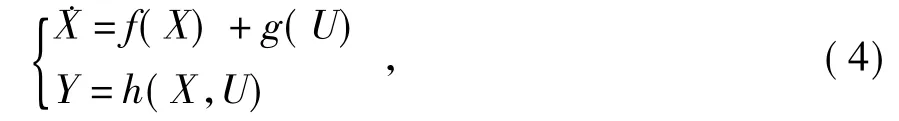
2 滑模控制

滑模控制主要目的是通過選取適當的狀態變量的線性組合組成切換面，然后通過引入李雅普諾夫函數來保證系統的正定性。

設狀態變量的跟蹤值為xref，則跟蹤誤差表達式為

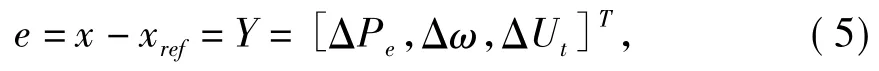
即系統的跟蹤誤差與系統的輸出相同。

定義滑模面為

式中:c=［c1，c2，c3］。滑模控制器的設計的主要任務之一就是行向量c的確定。

定義對應的李雅普諾夫函數為

針對三階系統，有 s=c1ΔPe+c2Δω +c3ΔUt，則

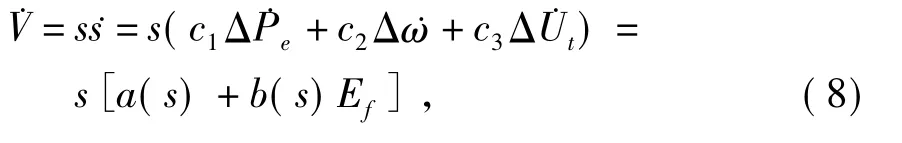
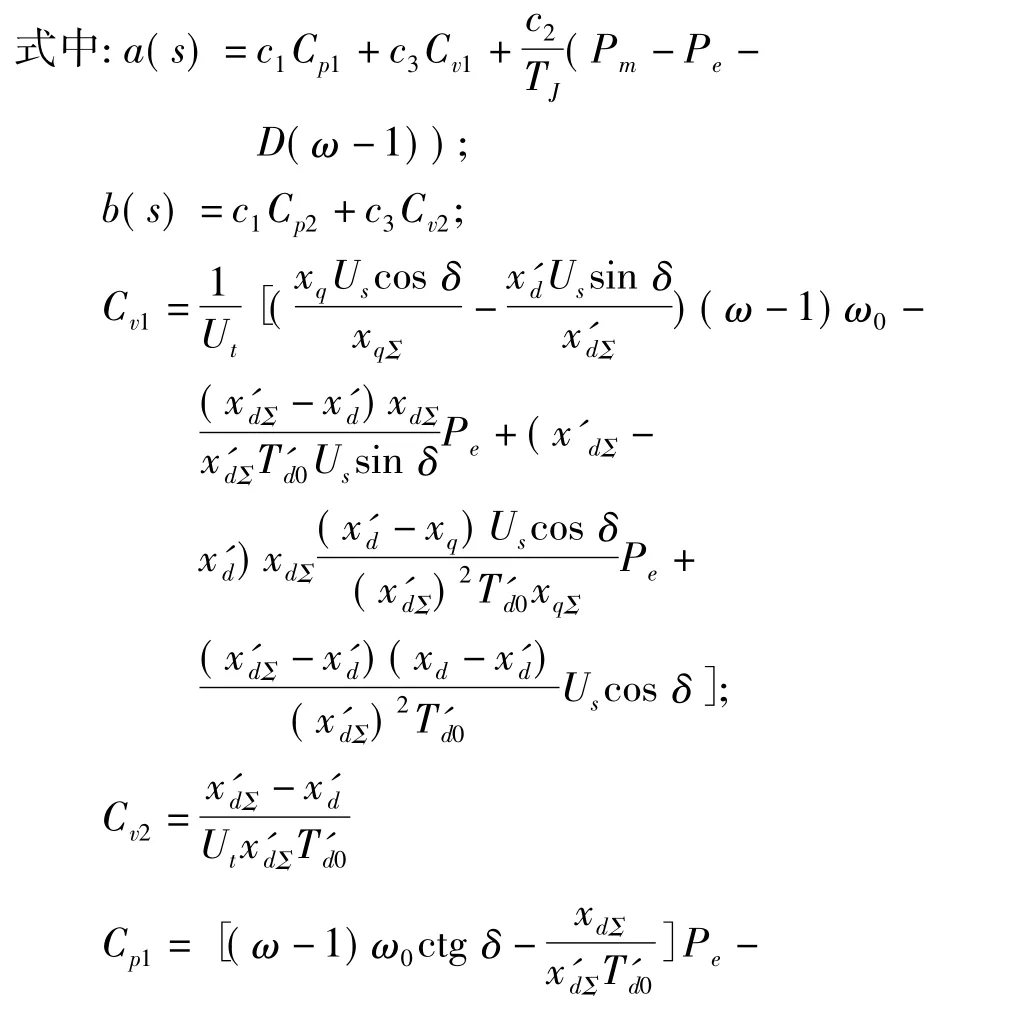
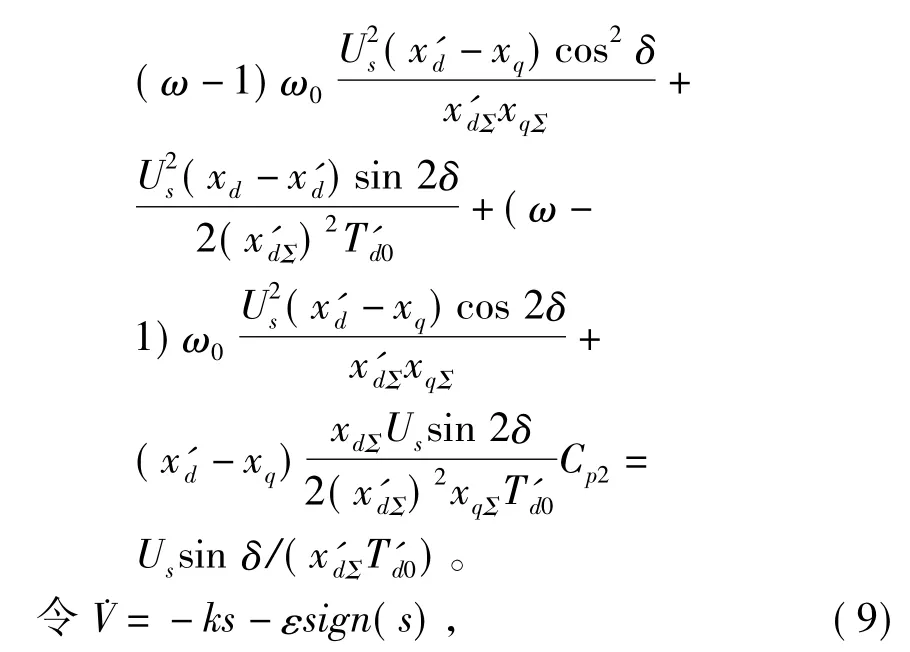
將式(7)代入式(6)，得

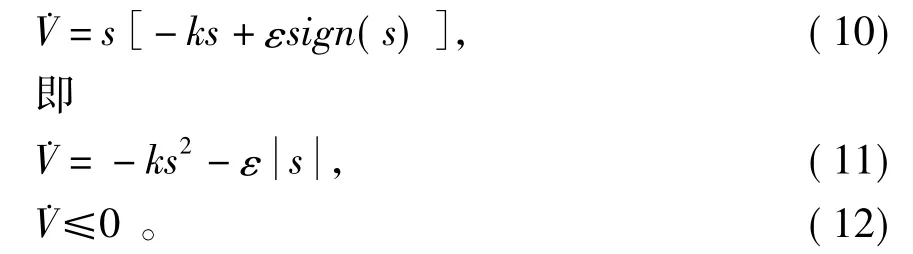
本文采用準滑動模態控制原理，即用飽和函數sat(s)代替滑動模態中的符號函數sign(s)，sat(s)的表達式為

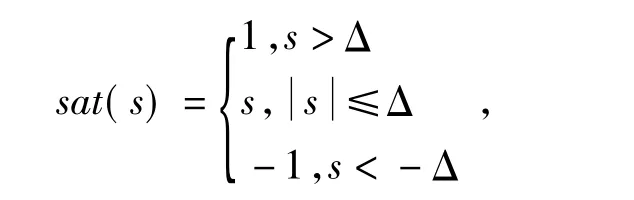
式中:Δ為邊界層。

經過替換之后的式(9)變為

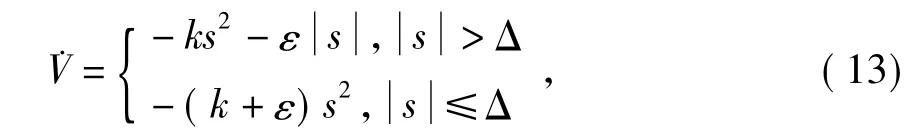
依然能夠保證導數的負定性，即由式(8)和式(9)，可以得出

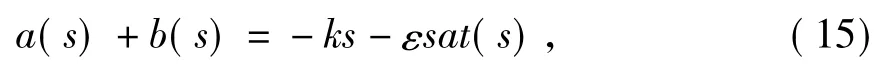
由(15)可以得出

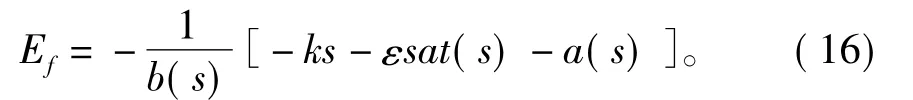
由于a(s)和b(s)的表達式比較復雜，含有較多的系統狀態變量和參數，所以通過ESO來觀測該部分，將其作為未知擾動部分處理。

3 擴張狀態觀測器(ESO)

因為系統的非線性變量包含在含有滑模面的一階方程中，所以只需構建二階的ESO即可，其表達形式為

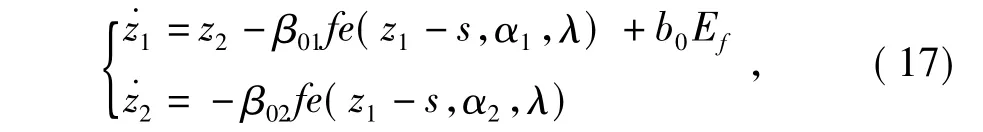
式中:z1為s的估計值;z2為擴張變量;

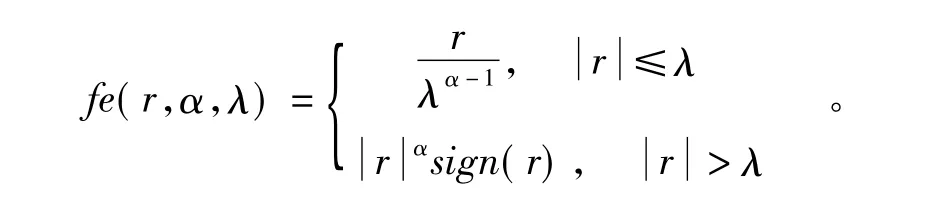
對于經過ESO反饋之后的式(8)所表示的系統控制輸入表達式為

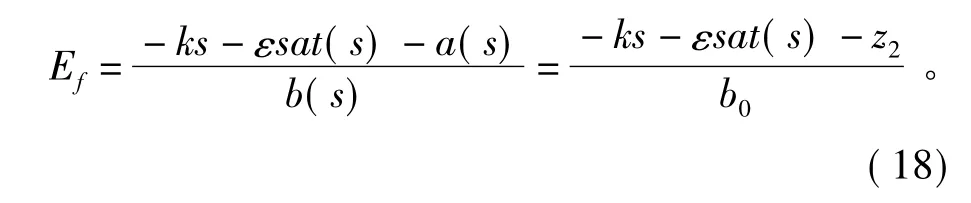
4 設計步驟和仿真分析

勵磁控制器的設計步驟如下:

1)選取新的坐標系和狀態變量e=Y=［Pe－Pe0，ω － ω0，Ut－ Ut0］T。

2)構造李雅普諾夫函數，并選取滑模面s=cY=c1ΔPe+c2Δω +c3ΔUt，并從其對應的導數式中得到滑模控制輸入的表達式為，其中R= －ks－εsat(s)。

3)構造二階的擴張狀態觀測器，得到對應的滑模控制器對應的控制變量

本文算例中單機無窮大系統的主要參數如下:

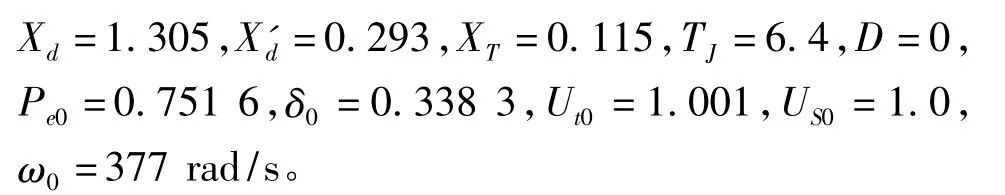
分別采用以下兩種勵磁控制器:

1)AVR+PSS，勵磁系統AVR采用機端電壓的偏差值作為輸入信號，PSS采用轉速的偏差作為輸入信號。

2)本文設計的勵磁控制器，其中ESO的參數

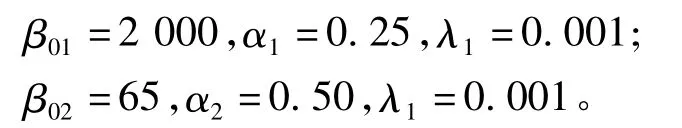
α1、α2、λ1的取法參見文獻［12］，β01、β02的確定可以根據z1－s目標函數，調用Simulink中的優化函數可得到。

滑模切換面的參數為

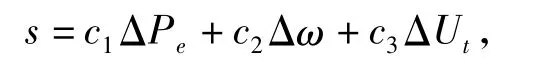
式中:c1=20;c2=－1 000;k1=22.22;c3=28;b0=0.28;ε1=0.2;Δ =0.1。參數 c1、c2、c3的選定可以使用極點配置法得到。

4.1 原動機輸入擾動

在0.1 s時，原動機的輸出功率Pm發生10%的階躍擾動，動態響應曲線分別如圖1、圖2所示，其中實線代表勵磁控制器，虛線則對應AVR+PSS控制器。

從圖1、圖2可以看出，在兩種不同勵磁控制器用下，圖中所示的勵磁控制器曲線均小于AVR+PSS。從仿真曲線上看，本文提出的勵磁控制器使功率振蕩受到一定的抑制。因此，該勵磁控制器能夠改善系統的小干擾穩定性。

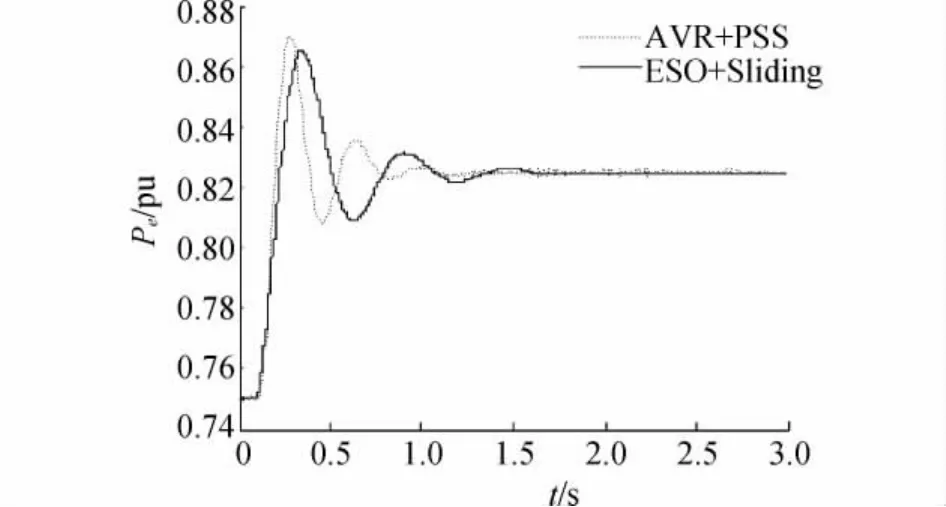
圖1 機械功率擾動時1號發電機電磁功率響應曲線

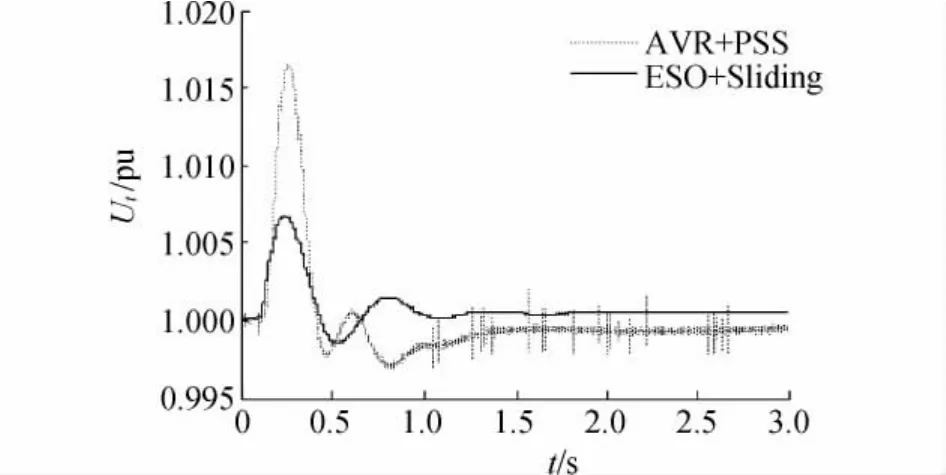
圖2 機械功率擾動時1號發電機機端電壓響應曲線

4.2 三相短路擾動

故障2為低壓側母線處0.1 s時發生瞬時三相短路，持續時間為0.1 s。有功功率Pe和機端電壓Ut的動態響應曲線分別如圖3、圖4所示。

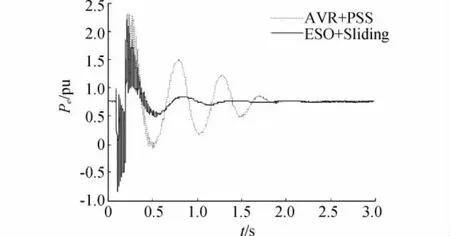
圖3 三相短路擾動時1號發電機電磁功率響應曲線

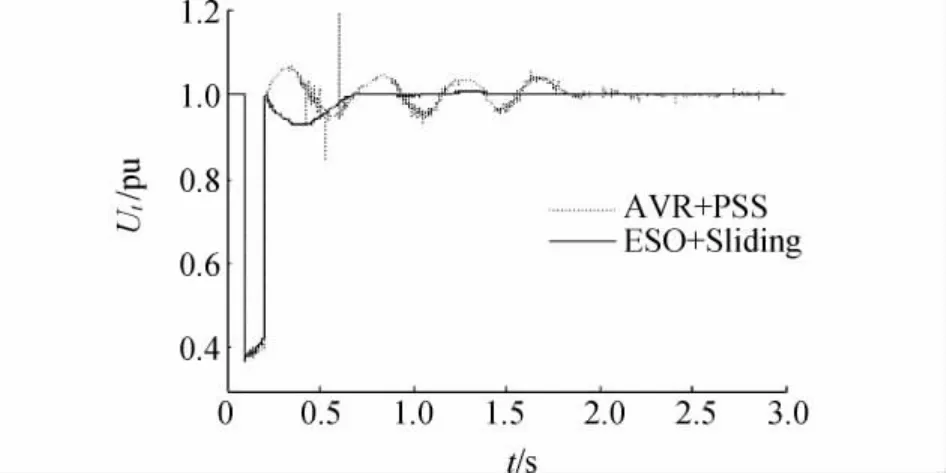
圖4 三相短路擾動時1號發電機機端電壓響應曲線

從圖3、圖4可以看出，在兩種不同勵磁控制器用下，功率振蕩時間分別為2.0 s、0.5 s。從仿真曲線上看，本文提出的勵磁控制器使狀態變量有效地抑制了振蕩幅值，減少了調節時間。因此，該勵磁控制器也可以改善系統的暫態穩定性。

5 結論

1)通過選取輸出函數中的跟蹤誤差可以得到對應的滑模切換面，使系統的狀態變量收斂于設定值。

2)李雅普諾夫函數的引入確保系統的整體穩定性，為控制器的設計提供了有利的依據。

3)擴張狀態觀測器的設計能夠抵消系統的擾動，不依賴與系統的運行狀態和參數，從而保證了控制器具有一定的魯棒性。

［1］周雙喜，汪興盛．基于直接反饋線性化的非線性勵磁控制器［J］．中國電機工程學報，1995，15(4):281 －288．

［2］蔡超豪．非線性H∞勵磁控制器的設計［J］．電網技術，2003，27(3):50－52．

［3］姚舜才，潘宏俠．粒子群優化同步電機分數階魯棒勵磁控制器［J］．中國電機工程學報，2010，30(21):91－97．

［4］張風營，朱守真．基于強跟蹤濾波器的自適應勵磁控制器［J］．中國電機工程學報，2005，25(23):31－35．

［5］萬黎，鄧長虹，陳允平．考慮機端電壓限制的多重非線性變結構勵磁控制［J］．中國電機工程學報，2008，28(19):86－92．

［6］張凱鋒，戴先中．多機電力系統勵磁控制的人工神經網絡逆系統方法［J］．中國電機工程學報，2003，27(21):24 －30．

［7］徐慶宏，戴先中．多機電力系統附加NNPSS的在線學習神經網絡逆勵磁控制器［J］．電力自動化設備，2010，30(1):25－31．

［8］蘭海，李殿璞，楊麗華．多機系統勵磁的非線性L2增益干擾抑制控制［J］．電機與控制學報，2005，9(2):151－155．

［9］王寶華．逆推自適應滑模勵磁控制器設計［J］．電力自動化設備，2009，29(6):54－57．

［10］鄒德虎，王寶華．發電機自適應Terminal滑模勵磁控制［J］．現代電力，2010 ，27(2):62－65．

［11］魯升敏．基于反推方法的滑模自適應勵磁控制［J］．電網與清潔能源，2010，26(1):77－79．

［12］韓京清．自抗擾控制技術［M］．北京:國防工業出版社，2008．