汽輪機(jī)靜葉柵二次流損失的數(shù)值研究

欒忠興，李勇，薛彥光，曹麗華

(1.大港油田濱海熱電廠，天津300280;2.東北電力大學(xué)能源與動(dòng)力工程學(xué)院，吉林吉林132012)

隨著現(xiàn)代科學(xué)技術(shù)的飛速發(fā)展，火電廠所用機(jī)組逐漸向大容量高參數(shù)轉(zhuǎn)變。葉柵中二次流損失在葉柵總損失中所占比例也越來越高，引起可觀的能量損失。上世紀(jì)60年代，人們就對(duì)葉柵內(nèi)二次流現(xiàn)象進(jìn)行研究，并做了大量的實(shí)驗(yàn)來驗(yàn)證。在國內(nèi)，相關(guān)文獻(xiàn)分析研究了葉柵二次流及渦系的發(fā)展特性，揭示出了葉柵前緣的馬蹄渦、流道內(nèi)的通道渦現(xiàn)象［1－2］。近年來，相關(guān)國外文獻(xiàn)對(duì)軸流式葉柵端壁邊界層二次流損失進(jìn)行了數(shù)值研究［3－5］。這些實(shí)驗(yàn)及數(shù)值研究豐富了二次流旋渦結(jié)構(gòu)，在一定程度上推動(dòng)了對(duì)葉柵內(nèi)部二次流損失機(jī)理的認(rèn)識(shí)。同時(shí)，大量研究證明，不同的葉柵幾何類型，其內(nèi)部渦系結(jié)構(gòu)的發(fā)展形態(tài)和損失部位也存在一定程度上的不同［6］。尤其是在二次流渦系研究方面，像壁角渦、尾跡渦這些小尺度渦很難被捕捉到［7］。因此研究并掌握二次流的形成原因、渦系結(jié)構(gòu)的演變特點(diǎn)對(duì)減少葉柵損失及改變?nèi)~柵的氣動(dòng)特性具有重要意義［8］。

本文通過對(duì)某汽輪機(jī)高壓級(jí)帶有一定扭曲度的靜葉柵進(jìn)行數(shù)值研究，得到了葉柵通道內(nèi)詳細(xì)的三維流場(chǎng)信息。準(zhǔn)確的捕捉到了流場(chǎng)內(nèi)部的壁角渦、尾跡渦等小尺度渦。計(jì)算出了葉柵速度場(chǎng)、壓力場(chǎng)的變化情況，以及沿流道總壓損失系數(shù)和靜壓系數(shù)的變化規(guī)律，比較分析了汽流在不同臨界狀態(tài)下的總壓損失系數(shù)、靜壓系數(shù)的變化規(guī)律及渦系的發(fā)展情況。對(duì)目前扭曲度葉柵的氣動(dòng)特性研究及設(shè)計(jì)具有極大的指導(dǎo)意義。

1 計(jì)算方法

1.1 湍流模型

由于k-ε湍流模型不能準(zhǔn)確的模擬剪切應(yīng)力的運(yùn)輸、回流以及流體的分離現(xiàn)象，因此采用了SST k-ω湍流模型，該模型是基于k-ω模型并結(jié)合k-ε雙方程模型而發(fā)展的一個(gè)新模型，它的混合功能實(shí)現(xiàn)了由邊界層內(nèi)部使用k-ω模型到邊界層外部使用k-ε雙方程模型的逐漸轉(zhuǎn)變，對(duì)近壁區(qū)的回流、存在逆壓力梯度的分離流能夠精確的預(yù)測(cè)。

1.2 數(shù)值計(jì)算方法

采用有限元的有限體積法，利用全隱式多網(wǎng)格耦合求解技術(shù)同時(shí)求解動(dòng)量方程和連續(xù)性方程。這種求解技術(shù)克服了傳統(tǒng)算法的假設(shè)壓力項(xiàng)、求解運(yùn)算、修正壓力項(xiàng)的反復(fù)迭代過程，其優(yōu)點(diǎn)是計(jì)算速度快、穩(wěn)定性好。

1.3 邊界條件

葉柵進(jìn)口按紊流邊界層1/7冪定律給定速度分布，中心速度約為150 m/s，進(jìn)口總溫為479℃，出口給定靜壓為10.54 Mpa;壁面給定壁面粗糙度，葉柵周向邊界上采用周期性邊界條件，葉柵型面粗糙度設(shè)為1.6 μm，上下端壁設(shè)為3.0 μm;進(jìn)口湍流強(qiáng)度設(shè)置Tu=5%;工質(zhì)選取IAPWS-IF97數(shù)據(jù)庫中的過熱蒸汽。

1.4 幾何模型及計(jì)算網(wǎng)格

計(jì)算所用幾何模型為某300 MW汽輪機(jī)高壓級(jí)靜葉柵，葉型具有一定扭曲度，主要幾何參數(shù)如下表所示:

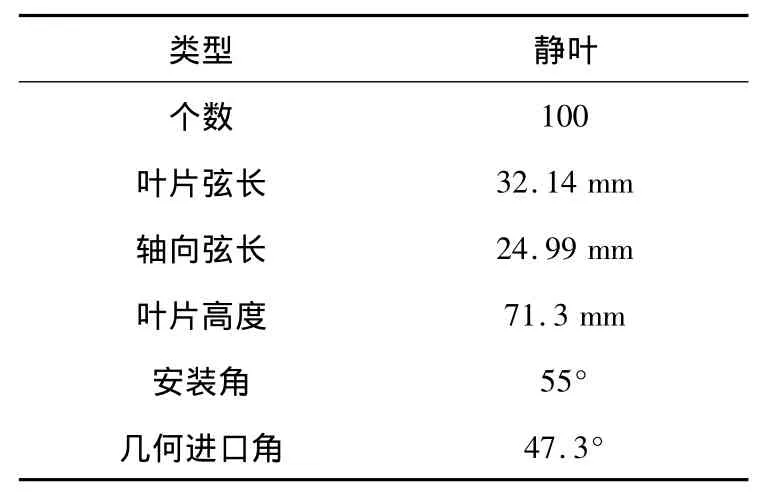
表1 靜葉柵主要幾何數(shù)據(jù)

計(jì)算采用結(jié)構(gòu)性六面體HOH型網(wǎng)格，葉型周圍采用O型網(wǎng)格加密技術(shù)，葉片上下端壁加入邊界層網(wǎng)格，網(wǎng)格總數(shù)為259 524，網(wǎng)格示意圖如圖1所示。

圖1 靜葉柵結(jié)構(gòu)性網(wǎng)格示意圖

2 計(jì)算結(jié)果分析

2.1 靜葉柵型面及下端壁流線分布

二次流是區(qū)別于主流而定義一種流動(dòng)，是指在葉柵通道上下端部的附面層內(nèi)，由于汽流速度相對(duì)很小，所產(chǎn)生的離心力不足以抵消從葉柵內(nèi)弧到背弧產(chǎn)生的橫向壓力差，在橫向壓力差作用下，上下端壁附面層的汽流便從葉柵內(nèi)弧向背弧橫向運(yùn)動(dòng)。

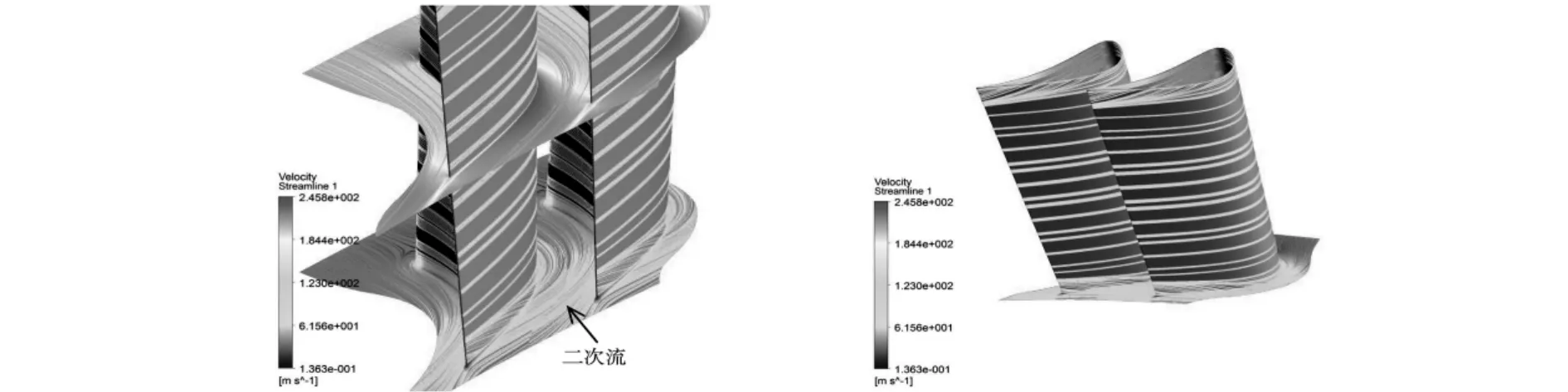
圖2 葉柵型面及端壁流線分布圖

圖2說明了在汽道中部，因汽流速度很大，葉片內(nèi)弧到背弧的橫向壓力差與離心力相互抵消，沒有引起主流的橫向流動(dòng);而在上下端壁的附面層內(nèi)，汽流速度很小，所產(chǎn)生的離心力不足以抵消內(nèi)弧到背弧產(chǎn)生的壓力差，產(chǎn)生了汽流的橫向運(yùn)動(dòng)。同時(shí)，在汽流流過汽道時(shí)，在上下端壁上由于蒸汽粘性的存在，形成了一層很薄的附面層，附面層內(nèi)的粘性力損耗了汽流的動(dòng)能，從而形成端壁摩擦損失。

圖3清楚的揭示了在葉柵通道內(nèi)的渦流特性，其中在葉柵前緣處形成的馬蹄渦和壁角渦，上下端壁處由于橫向壓力梯度存在而形成的通道渦，以及內(nèi)弧和背弧處形成的壁角渦。

壁角渦的形成原因是葉柵背弧附面層的不斷增厚，同時(shí)與上下端壁上的橫向來流的附面層相匯合，厚度急劇增加，造成附面層的脫離進(jìn)而形成方向相反的兩個(gè)旋渦，隨后在粘性力的影響下，旋渦被主流帶出葉柵，引起可觀的能量損失。

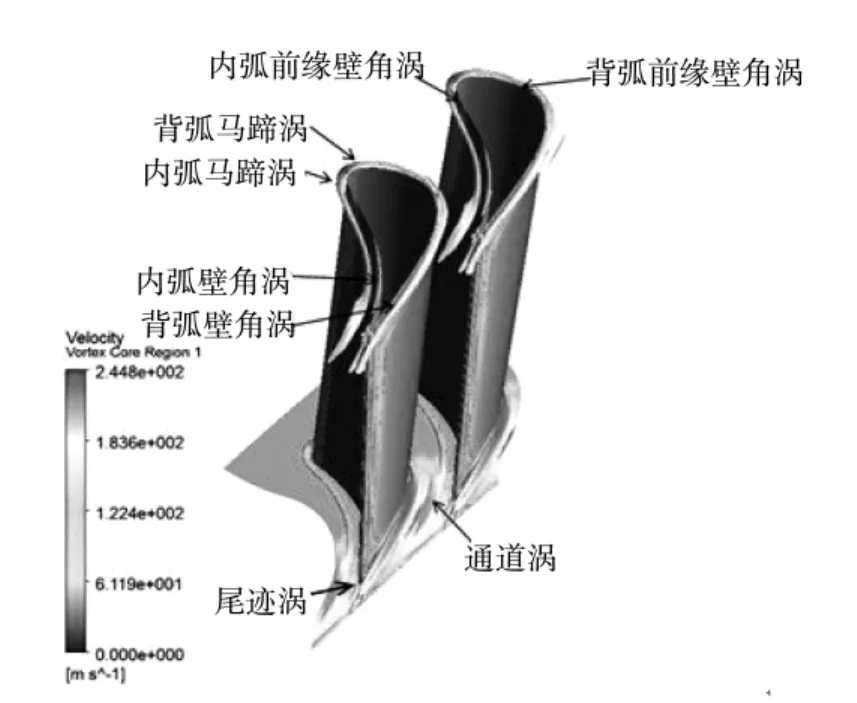
圖3 靜葉渦流示意圖

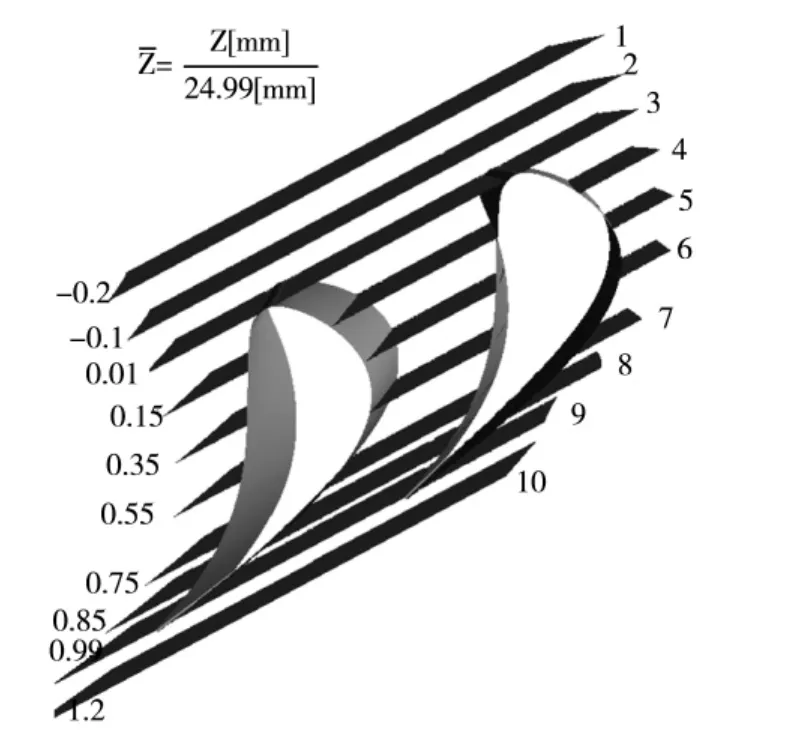
圖4 葉柵不同測(cè)量截面位置

3.2 沿流向總壓損失系數(shù)、靜壓系數(shù)分布特性

為了更準(zhǔn)確的揭示端壁二次流的損失情況以及對(duì)流場(chǎng)的影響，引入總壓損失系數(shù)［9］Cpt和靜壓系數(shù)［10］Cps的概念。

式中:Cpt為總壓損失系數(shù)，Pa;Cps為靜壓系數(shù)，Pa;patm為大氣壓，Pa;pot為進(jìn)口總壓，Pa;pt為流場(chǎng)內(nèi)各點(diǎn)總壓，Pa;ps為流場(chǎng)內(nèi)各點(diǎn)靜壓，Pa;ρout為出口汽流按出口截面面積平均密度，kg/m3;uout為出口汽流按出口截面面積平均速度，m/s;ρin為進(jìn)口汽流按出口截面面積平均密度，kg/m3;uin為進(jìn)口汽流按出口截面面積平均速度，m/s。

為分析端部二次流在流道內(nèi)的發(fā)展情況，在葉柵通道內(nèi)部沿軸向分隔出10個(gè)不同的測(cè)量截面(如圖4)，其中每個(gè)截面對(duì)應(yīng)一個(gè)值。

圖5(a)中，從總體趨勢(shì)上看，總壓損失系數(shù)沿流向逐漸增大，在背弧面上總壓損失系數(shù)出現(xiàn)先增后減現(xiàn)象;而在內(nèi)弧處出現(xiàn)先增后減再增現(xiàn)象。

為更好的分析葉柵通道中總壓損失系數(shù)分布情況，結(jié)合圖4中的10個(gè)截面進(jìn)行比較分析。在截面3(=0.01)處總壓損失系數(shù)比較小，且內(nèi)弧損失大于背弧損失。截面3(=0.01)和截面4(=0.15)之間內(nèi)弧總壓損失系數(shù)出現(xiàn)拐點(diǎn)并開始減小。截面4(=0.15)處背弧和內(nèi)弧總壓損失系數(shù)相等，在此之后背弧總壓損失系數(shù)開始大于內(nèi)弧并迅速增加，而后在截面7(=0.75)處達(dá)到最大值;而在截面7(=0.75)處，內(nèi)弧總壓損失系數(shù)由原來的緩慢增長變?yōu)榧彼僭鲩L。

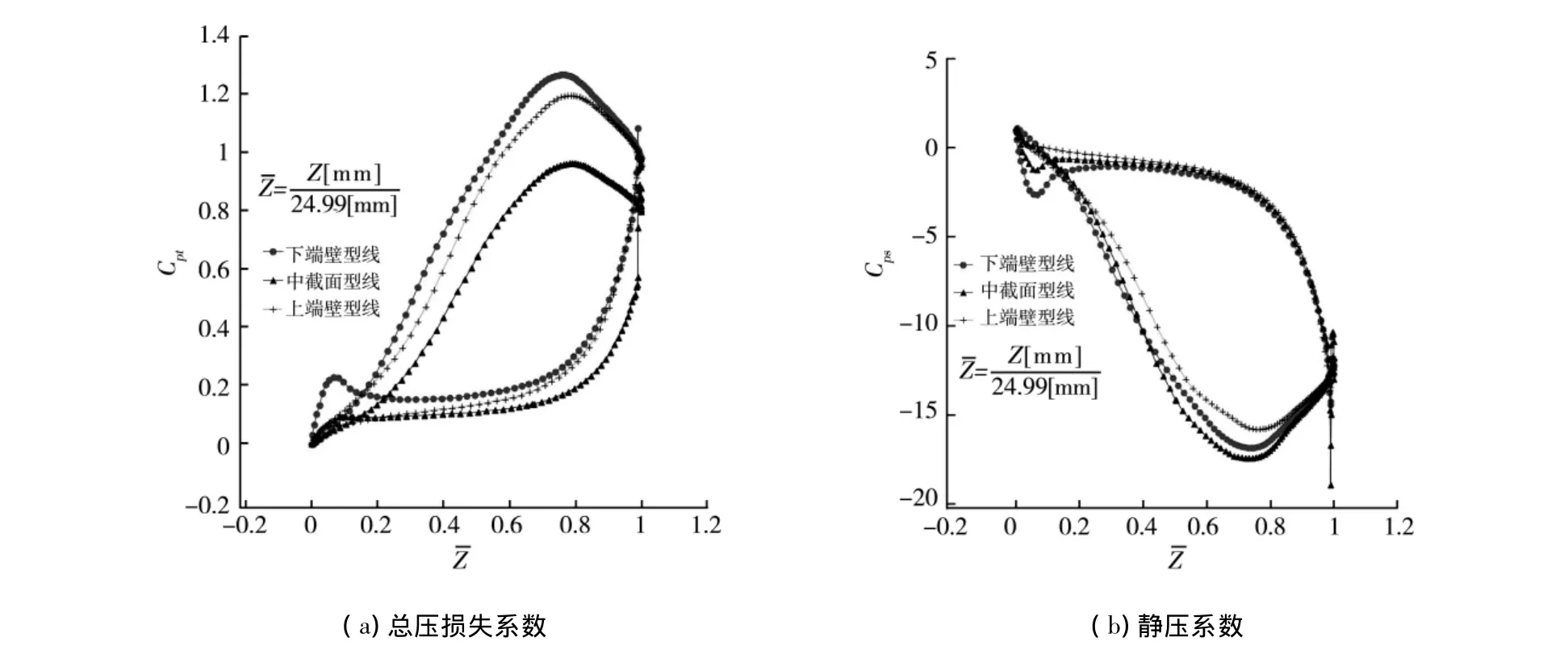
圖5 葉柵總壓損失系數(shù)和靜壓系數(shù)沿流向分布

產(chǎn)生這種現(xiàn)象的原因主要有兩方面，一方面是與葉柵型線有關(guān)，另一方面是由于在汽道中存在從內(nèi)弧到背弧的橫向壓力梯度，使得端壁附面層內(nèi)的低能流體向背弧移動(dòng)，背弧損失區(qū)增厚。隨著流動(dòng)向下游發(fā)展，當(dāng)?shù)湍芰黧w被卷吸到背弧上時(shí)，使得上下端壁的低能流體在展向流動(dòng)并與之發(fā)生相遇、摻混，使背弧附面層驟然增厚，損失增加迅速，在截面7(=0.75)處流體已處在由葉柵喉部向出口運(yùn)動(dòng)的過程中，因擴(kuò)壓作用使得背弧總壓損失系數(shù)也達(dá)到最大。在向下游的運(yùn)動(dòng)過程中，由于低能流體的橫向流動(dòng)，在靠近端壁的內(nèi)弧附近必然會(huì)有少量的主流流體進(jìn)行補(bǔ)償，造成內(nèi)弧總壓損失系數(shù)的急劇增加。

從圖5(b)中可以看出，靜壓系數(shù)分布曲線與總壓損失系數(shù)分布正好相反，其原因見上述分析。

3.3 不同測(cè)量截面總壓損失系數(shù)和汽流角沿葉高分布

影響二次流損失大小的因素有沿葉高不變的葉型損失、沿葉高變化的端部損失，其中最主要的因素是葉柵高度與葉柵弦長的比值大小。因此，對(duì)于總壓損失系數(shù)沿葉高變化的研究有一定意義。

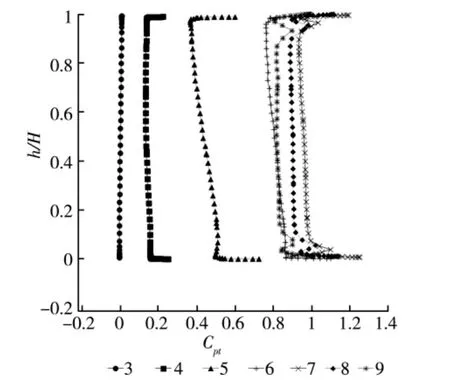
圖6 不同測(cè)量截面總壓損失系數(shù)沿葉高分布

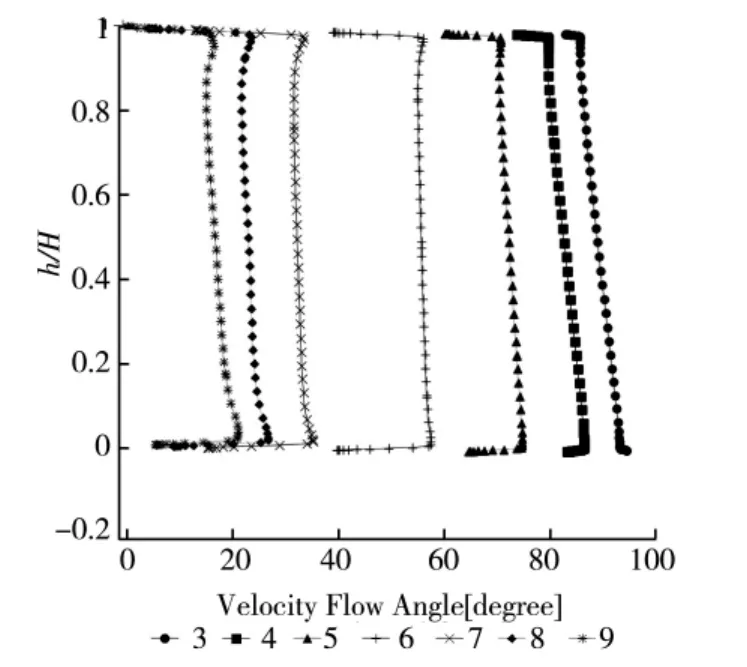
圖7 不同測(cè)量截面汽流角沿葉高分布

圖6為不同測(cè)量截面(圖5中定義的)與葉柵背弧交線處總壓損失系數(shù)沿葉高分布規(guī)律，大的總壓損失系數(shù)首先在近壁區(qū)產(chǎn)生，且在上下邊界層有明顯不均勻特性，這主要是由于上下端部邊界層存在粘性作用;隨著流動(dòng)向下游發(fā)展，總壓損失系數(shù)沿流向方向也在不斷增加，大的總壓損失系數(shù)也沿葉高方向增加并最終向葉柵中部發(fā)展。在截面7(=0.75)處，由于進(jìn)入擴(kuò)壓階段，總壓損失系數(shù)在上下端壁處變化劇烈，對(duì)整個(gè)通道的損失分布產(chǎn)生較大影響。由此可知，在上下端部截面以及葉柵內(nèi)弧、背弧的總壓損失系數(shù)分布，清晰的說明了附面層內(nèi)的低能流體所引起的橫向流動(dòng)、附面層卷起、堆積等流動(dòng)特性。

圖7為不同測(cè)量截面(圖5中定義的)與1/2截距面交線處汽流角沿葉高分布規(guī)律，由圖可知，在每一個(gè)截面上，汽流角在中部變化平穩(wěn)，在上下端壁處存在過偏轉(zhuǎn)和欠偏轉(zhuǎn)的特性。過偏轉(zhuǎn)是近壁汽流在上下端壁附近內(nèi)弧與背弧壓差作用下產(chǎn)生橫向流動(dòng)的結(jié)果，欠偏轉(zhuǎn)是一部分主流汽體被通道渦卷吸而產(chǎn)生的由葉柵內(nèi)弧向背弧流動(dòng)的速度分量，及葉柵背面附近積聚的低能流體對(duì)主流的排擠而形成的。

4 結(jié)論

(1)在葉柵型面和上下端壁面上加了邊界層，并考慮了壁面粗糙度的影響。用有限體積法和SST k－ω湍流模型模擬靜葉柵通道內(nèi)存在的復(fù)雜流動(dòng)是有效的，此方法能夠精確的顯示近端壁區(qū)的二次流現(xiàn)象，準(zhǔn)確的捕捉到了近壁面區(qū)的渦流特性。

(2)沿葉柵流動(dòng)方向，總體上總壓損失系數(shù)沿流向逐漸增大，在背弧上總壓損失系數(shù)出現(xiàn)先增后減現(xiàn)象，而在內(nèi)弧上出現(xiàn)先增后減再增現(xiàn)象;靜壓系數(shù)與之相反。

(3)沿葉高方向，大的總壓損失系數(shù)首先在近壁區(qū)產(chǎn)生，在葉柵流道上下端壁處變化非常明顯，主要是由于附面層內(nèi)的低能流體所引起的橫向流動(dòng)、附面層卷起、堆積造成的。

(4)沿葉高方向，汽流角在中部變化平穩(wěn)，在葉柵流道上下端壁區(qū)出現(xiàn)過偏轉(zhuǎn)和欠偏轉(zhuǎn)現(xiàn)象。

［1］葉大均，周禮蔚.渦輪葉柵二次流損失的實(shí)驗(yàn)研究［J］.工程熱物理學(xué)報(bào)，1985，6(2):130－135.

［2］王仲奇，馮國泰，王松濤，等.透平葉片中的二次流旋渦結(jié)構(gòu)的研究［J］.工程熱物理學(xué)報(bào)，2002，23(5):553－556.

［3］R.A.Graziani，Blair M.F.，Taylor J.R.and Mayle R.E.An Experimental Study of Endwall and Airfoil Surface Heat Transfer in a Large Scale Turbine Blade Cascade［J］.Journal of Engineering for Power，1980，102:257－267.

［4］Piotr Lampart.Investigation of endwall flows and losses in axial turbines:part 1.Formation of endwall and losses［J］.Journal of Theoretical and Applied Mechanics，2009，479(2):321－342.

［5］Hermanson K S，Thole K A.Effect of inlet conditions on endwall secondary flows［J］.Journal of Propulsion and Power，2000，16(2):286－296.

［6］李軍.用CFD研究渦輪靜葉柵的二次流損失［J］.燃汽輪機(jī)技術(shù)，2007，20(4):43－46.

［7］林奇燕，鄭群，岳國強(qiáng).葉柵二次流旋渦結(jié)構(gòu)與損失分析［J］.航空動(dòng)力學(xué)報(bào)，2007，22(9):1518－1524.

［8］郭緒，俞茂錚.直列透平靜葉柵二次流動(dòng)的數(shù)值模擬［J］.汽輪機(jī)技術(shù)，1998，40(6):342－347.

［9］Yamamoto A.Production and development of second2ary flows and losses within two types of straight turbine cascade:part 1［J］.ASME Journal of Turbomachinery，1987，109(4):194－200.

［10］A.yangyozoy R.Willinger.Calculation of flow Characteristics in Heat Turbomachinery Turbine Stage With Different Three Dimensional Shape of The Stator Blade With Ansys-cfx Software［J］.Institute for Thermodynamics and Energy Conversion，2008，11(2):42－54.