脫硫塔內氣固流場數值模擬－稠密顆粒動理學方法

鄭建祥，呂太

(東北電力大學能源與動力工程學院，吉林吉林132012)

循環流化床煙氣脫硫技術，具有造價低、脫硫效率適中、適合機組改造、用水量少，不產生二次廢水等優點，已經成為我國優先推廣使用的煙氣脫硫技術之一。該技術存在脫硫劑利用率低，脫硫塔體負荷適應性不強的缺點［1］。采用內循環噴動流化可以有效解決上述問題［2］。因此，噴動床內高濃度氣固兩相流動行為的研究愈顯重要。盡管國內外對噴動床內氣固兩相運動進行了大量實驗研究，并取得了一定的進展，但噴動床內氣體和顆粒流動特性的數值模擬研究工作卻很少［3－4］。

本文基于顆粒動理學理論、引入顆粒相動力－摩擦應力模型，預測噴動床內流體動力行為。模型中采用Johnson-Nott［5］提出的摩擦應力模型考慮顆粒間滾動－滑動摩擦產生的正應力和由Guenther-Syamlal等［6］提出的摩擦剪切粘度模型考慮顆粒間滾動－滑動摩擦產生的切應力，研究噴動床內顆粒間相互作用對氣固兩相宏觀流動特性的影響。數值模擬噴動床內氣固流動特性。模擬結果可對脫硫塔結構的優化設計提供參考。

1 數學模型

連續性方程(k=g時為氣相，k=s時為顆粒相)

其中，ρk為k相密度;εk表示相體積濃度;vk為相速度;t為時間。

氣相動量守恒方程

其中，Pg為氣相壓力;g為重力加速度;β為氣固相間曳力系數;τg為氣相應力張量。其中氣相應力張量τg為

其中:μg，1為氣體層流動力粘度;μt為氣體湍流動力粘度。假定氣體不可壓縮，密度為常量。氣相湍流采用大渦模擬方法，即對氣相大尺度渦直接求解N－S方程，而小尺度渦通過建立SGS湍流模型求解，氣相動力粘性系數［6］

其中:c是Smagorinsky常數，取值為0.1;Δ為網格空間尺度;i、j為對應的網格坐標分量。

固相動量方程

假設顆粒應力張量τs為動力應力張量τk和滾動－滑動摩擦應力張量τf之和，即

采用Guenther-Syamlal等［6］提出的滾動－滑動摩擦切應力模型，μkinetic和滾動－滑動摩擦剪切粘度μfriction之和，即μs=μkinetic+μfriction可表示為

其中:d為顆粒直徑;e為顆粒彈性恢復系數;go為徑向分布函數;D為應變率;εs，max和εs，min分別為填充顆粒濃度和臨界顆粒濃度;n和p分別為與顆粒材料物性有關的經驗系數;θ為內摩擦角，對于玻璃珠顆粒參數n、p和分別為2.0、5.0和28.5°。

顆粒壓力ps表示由于顆粒非彈性碰撞等相互作用產生的正應力。在高顆粒濃度下顆粒壓力除了考慮顆粒碰撞產生的動力應力外，還需要考慮顆粒滾動－滑動磨擦作用的貢獻。動力應力分量由顆粒動理學確定，顆粒間滾動－滑動磨擦產生的正應力按Johnson-Nott［5］提出的滾動－滑動摩擦應力模型計算。則顆粒壓力可表示為

其中:Fr為與顆粒材料物性有關的經驗系數。對于玻璃珠顆粒參數Fr為0.05。

方程(8)和(9)中為顆粒溫度，定義為θ=C2/3，其中，C為顆粒脈動速度。顆粒溫度可按固相脈動能量守恒方程確定為

其中:ks為固相脈動能量傳遞系數;γs為顆粒碰撞能量耗散率。

顆粒碰撞能量耗散率:

固相脈動能量傳遞系數:

其中:go徑向分布函數按下式計算［7］:

相間動量交換系數β按下式計算［4］:

其中:Re為雷諾數，Re=dρgUg－Us/μg。

2 進出口邊界及初始條件

給定入口處壓力，出口處壓力梯度取為零。入口處，各相速度給定。床內各相初始速度設為零。

壁面邊界條件對氣相，壁面采用無滑移邊界條件。壁面處顆粒速度和顆粒溫度采用下列方程［8］:

其中:n為從邊界指向顆粒群的單位法向量;δ為材料摩擦角;φ'為鏡面反射系數;模擬中取為0.5;ew為壁面彈性恢復系數;vsl為顆粒的滑移速度，即顆粒群速度與壁面速度之差vsl=vs－vwall。

圖1表示模擬來源于何玉榮［9］模擬數據。內徑152 mm，高1 140 mm，堆積床料高33 0mm。顆粒直徑和顆粒密度分別為1.0 mm和1 200 kg/m3。顆粒間及顆粒與壁面間彈性碰撞恢復系數均取為0.5。計算總時間為30 s，最后25 s作為時間平均值的計算樣本。

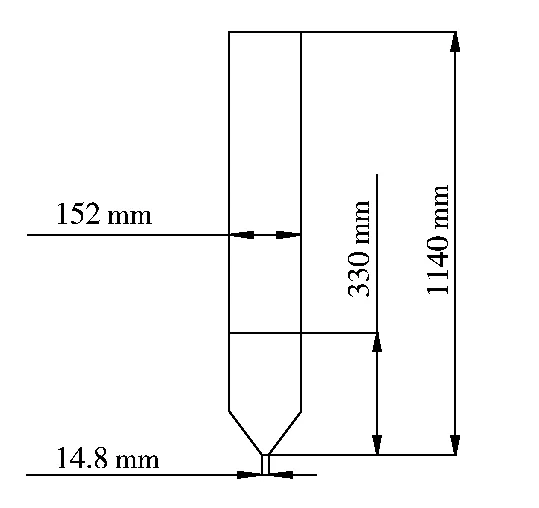
圖1 噴動床計算模型的幾何結構

3 模擬結果及討論

圖2表示入口速度為v=15 m/s下不同時刻瞬時濃度圖。由圖可見，在噴射區內，顆粒濃度低;在環隙區內，顆粒濃度高。在噴射區內，氣體夾帶顆粒和向上流動，到達噴射出口，由于中間噴射氣流速度很高，因此從噴射區噴出得顆粒和被氣體揚析出去，分布于床中上部區形成典型的噴泉區。在噴射區上方氣速降低，加之重力的因素，顆粒和返回床面，并沿著環隙區向下流動，再滲透至噴射區被氣體重新攜帶向上流動，從而形成有規律的內循環流動。

圖2 不同時刻濃度圖

圖3表示入口氣體速度為15 m/s時不同高度時均顆粒濃度分布。由圖可見，無因次半徑x/D=0處表示噴動床中心位置，x/D=－0.5表示壁面區域。中心區域濃度最低，在壁面處由于顆粒回流作用使得時均顆粒濃度又增大。隨著高度的提高，濃度整體變小。

圖3 不同高度顆粒濃度分布

圖4 不同噴動速度下徑向顆粒濃度分布

圖4分別表示不同進口速度對顆粒濃度影響。由于速度增加，從噴射區滲透到環隙區氣體增多，床層膨脹較高，顆粒流動更加均勻。

4 結論

考慮高濃度顆粒間的滾動－滑動磨擦作用，應用顆粒動力學模型建立顆粒相稠密顆粒動理學模型模擬顆粒相流動，采用應用大渦模擬研究氣相流動，對脫硫塔噴動顆粒流化過程進行了數值模擬，得到了噴動床內顆粒的流化過程。模擬計算結果表明，噴動床流化形成典型的環隙區，噴射區，噴泉區流動狀態。適當的進口速度有助于形成穩定噴動。

［1］董勇.煙氣脫硫循環流化床內物料分離循環的研究［D］.哈爾濱:哈爾濱工業大學，2004.

［2］Josefa F，Jose L R，Hipo G，et al.Development of Sorbents for SO2 Capture Prepared by Hydration of Fly Ash and Hydrated Lime in Seawater［J］.Ind.Eng.Chem.Res.2006(45):856－862.

［3］Xu C.，Zhu J.Experimental and Theoretical Study on the Agglomeration Arising from Fluidization of Cohesive Particles-effects of Mechanical Vibration［J］.Chemical Engineering Science，2005，60:6529－6541.

［4］陸慧林，劉文鐵，劉歡鵬，劉鵬.流化床內超細顆粒的流動［J］，工程熱物理學報，2003，24(3):534－536.

［5］Johnson P C，Nott P，Jackson R，Frictional-collisional Equations of Motion for Particulate Flows and Their Application to Chutes［J］.J.Fluid Mech.，1990，210:501－535.

［6］Guenther C，Syamlal M，The Effect of Numerical Diffusion on Simulation of Isolated Bubbles in A Gas-solid Fluidized Bed［J］，Powder Technology，2001，116:142－154.

［7］Bagnold R.A.Experiments on A Gravity-free Dispersion of Large Solid Spheres in A Newtonian Fluid Under Shear［J］.Proc.R.Soc.London，1954，A225:49－63.

［8］Koch D.L，Sangani A.S.Particle Pressure and Marginal Stability Limits for a Homogenous Monodisperse Gas-fluidized Bed:Kinetic theory and numerical simulations［J］.J.Fluid Mech，1999，400:229－263.

［9］何玉榮.流化床內高濃度氣固兩相流動特性數值模擬研究［D］.哈爾濱:哈爾濱工業大學，2004:44－50.