保費隨機收取的二維風險模型的破產概率

黃玉娟,于文廣

（1.山東交通學院理學院，濟南250023;2.山東財經大學保險學院，濟南250014）

0 引言

在經典的保險風險理論中，復合泊松風險模型U(t)=u+ct-S(t)是主要的研究對象，并且取得了許多經典的結果[1][2]。隨后許多學者對該風險模型進行了各種各樣的推廣，其中之一就是將一維模型推廣到多維風險模型。近年來隨著保險數學的研究，多維風險模型也越來越受到關注，但是多維風險模型在數學處理上較為復雜，即便是二維風險模型在技術處理上也較為困難。文獻[3]構造了一個二維風險模型，定義了三類破產概率，給出了關于破產概率的一個簡單的界，得到了理賠額服從phase-type分布時的破產概率的確切表達式。文獻[4]對多維風險模型破產概率進行了研究，并將同一索賠事件產生的幾種索賠之間的相關關系考慮了進來，應用多維Phase-type分布得到了幾種不同形式破產概率的邊界。文獻[5]、[6]研究了索賠相關的雙Poisson二維風險模型的破產概率。文獻[7]、[8]分別討論了索賠為輕、重尾分布的二維風險模型的破產概率。文獻[9]把索賠到達過程推廣到Poisson過程且每份保單的理賠額也推廣為隨機變量,得到了相關風險模型的破產概率及其上界。基于上述文獻，本文將稀疏過程引入到二維風險模型中，將收取新保單和由續保收到的保單區別開來，即索賠以Poisson流到達到的同時會產生一個強度為λρ(0＜ρ＜1)續保的Poisson過程，同時新保單也以Poisson流到達。

1 模型的定義與實際背景

定義1設u1≥0，u2≥0，c＞0，α＞0，在給定概率空間(Ω,F,P)上，定義二維風險模型為：

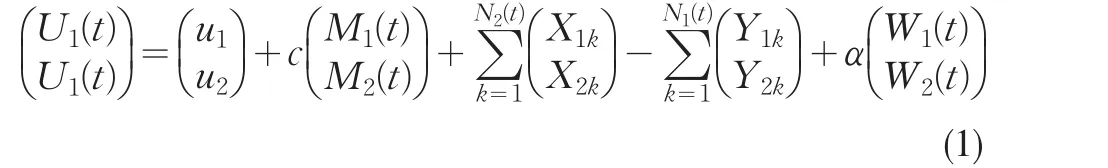
其中，ui≥0是第i個保險公司盈余過程{Ui(t);t≥0}的初始資本，i=1,2；c為單位時間內收到的保費；{Wi(t);t≥0}為一標準維納過程，表示第i個保險公司的不確定的收益和支付，i=1,2；α為大于零的常數，表示擴散擾動強度。{Mi(t);t≥0}為直到t時收到的新保單數，服從參數為 βi的泊松過程，i=1,2；{N1(t);t≥0}表示[0,t]內的總理賠次數，其速率為 λ1的泊松過程；{Yik≥0;k=1,2,...}表示第i類險種第k次的理賠額，且獨立同分布，E[Yik]=μiy，Var[Yik]=σ2iy，i=1,2；{Xik≥0;k=1,2,...}表示第i類險種第k次續保費，且獨立同分布，E[Xik]=μix，Var[Xik]=σ2ix，i=1,2，并設μiy＞μix；{N2(t);t≥0}表示[0,t]內續保保單以速率λ1ρ (0＜ρ＜1)的泊松過程到達，即{N2(t);t≥0}是{N1(t);t≥0}的ρ-稀疏過程。ρ的實際意義為考慮這樣一類險種，它由兩個相關的風險類構成。每一類都有兩種理賠方式，主理賠與次理賠，即某一類風險理賠的發生會以某概率ρ的可能性產生次理賠。例如，在一次交通事故中，車輛發生意外造成損壞，同時人身也可能受到傷害，那么可以把車險看作主理賠，人身保險看作次理賠。

令

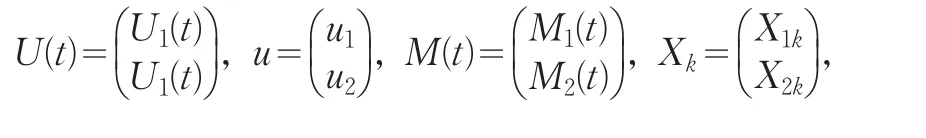
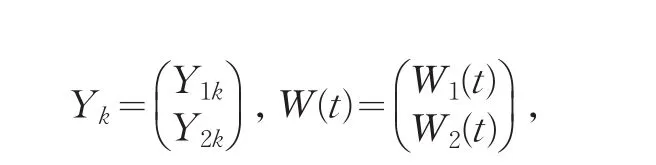
則(1)式可以改寫為

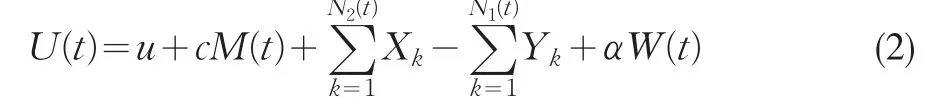
假設1{N1(t);t≥0}與{Yk≥0;k=1,2,...}、{Xk≥0; k=1,2,...}、{M(t);t≥0}和{W(t);t≥0}是相互獨立的。{Y1k≥0;k=1,2,...}和 {Y2k≥0;k=1,2,...}相互獨立；{X1k≥0;k=1,2,...}和{X2k≥0;k=1,2,...}相互獨立。

以上我們定義了稀疏過程下的二維風險模型，但二維風險模型的破產定義與一維風險模型的情況是有區別的。首先，給出一維風險模型兩個盈余過程{U1(t);t≥0}和{U2(t);t≥0}的破產時刻和破產概率的定義。定義Tj為第 j個盈余過程的破產時間 j=1,2，即Tj=inf{t|Uj(t)＜0}及第 j個盈余過程的破產概率ψj(uj)= Pr(Tj＜∞|Uj(0)=uj)。

下面給出二維風險模型的三類破產時刻的定義：

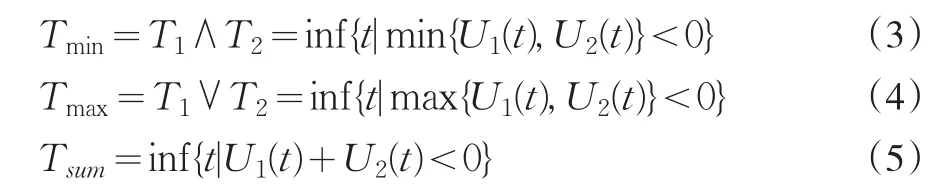
相應的破產概率分別定義為：

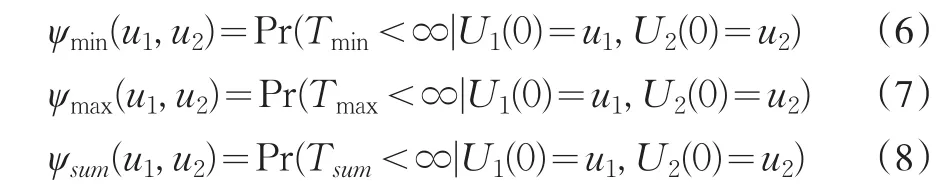
注以上定義的實際背景為，{Tmin＜∞}表示U1(t)和U2(t)中至少有一保險公司的盈余過程為負值，即在將來的某個有限時刻t，至少會有一個保險公司發生破產；{Tmax＜∞}表示在將來某個有限時刻t，其盈余U1(t)和U2(t)都會為負值，即兩個保險公司在將來有限時刻t均會發生破產；{Tsum＜∞}表示U1(t)與U2(t)的和會為負值，即兩個風險過程的和將來在有限時刻t會為負值，即破產發生。因此，與一維保險風險模型相比，其破產概率滿足如下關系：

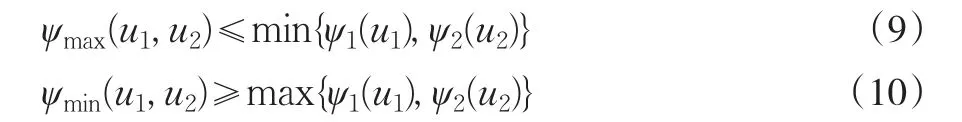
且根據定義有

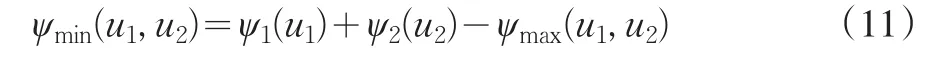
下面對Tmin進行討論。首先考慮其對應的生存概率：

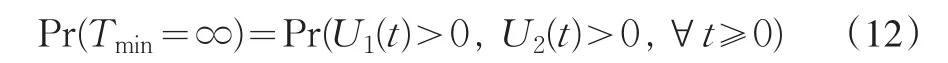
引理1給定兩個實數{x1,x2}，則如果它們都為嚴格正值當且僅當對所有嚴格正實數{a1,a2}，都有 a1x1+a2x2＞0。事實上，引理條件只需要a1＞0, a2＞0及a1+a2=1。

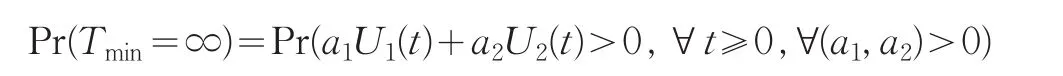
所以，由引理1和(12)式可知：下面定義一個參數為a={a1,a2}的一維風險模型：

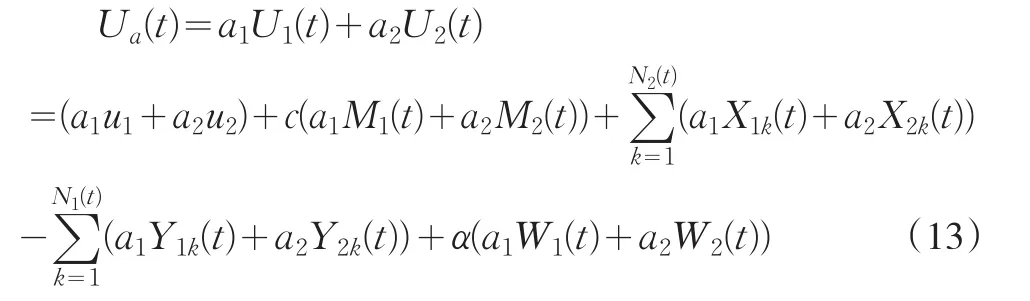
令

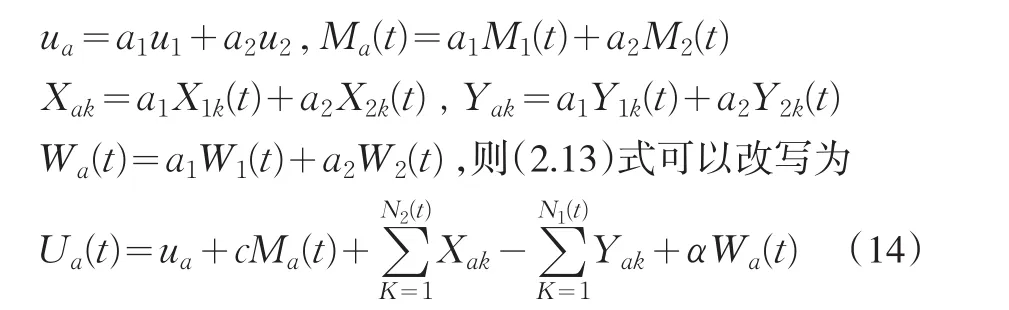
定義盈余過程{Ua(t);t≥0}的破產時刻為Ta=inf {t≥0|Ua(t)＜0}，則其想應的破產概率定義為：

運用現代概率論相關知識，可得Tmin和Ta如下關系：

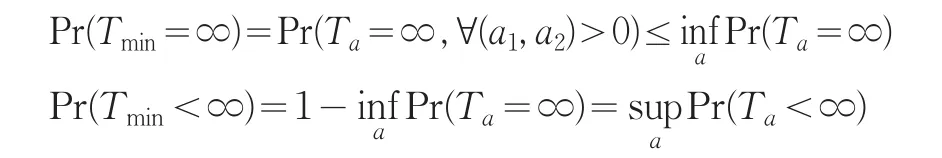
類似地，(7)式中定義的破產概率ψmax(u1,u2)滿足：

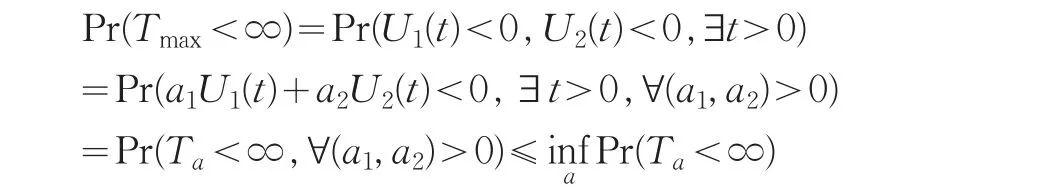
特別的，當 a1=1/2,a2=1/2，可以得到 Pr(Tsum＜∞)=Pr(T{1/2,1/2}＜∞)。因此，破產概率Pr(Tsum＜∞)可以簡化為一維風險模型的破產概率。

2 主要結果

定理1盈利過程{Sa(t),t≥0}具有下列性質：

(1)Sa(0)=0;(2){Sa(t),t≥0}平穩獨立增量；(3)存在正數r＞0，使得E[exp(-rSa(t))]＜∞。

定理2對于盈利過程{Sa(t),t≥0}，存在函數g(r)使得E[exp(-rSa(t))]=exp(tg(r))。

證明：E[exp(-rSa(t))]

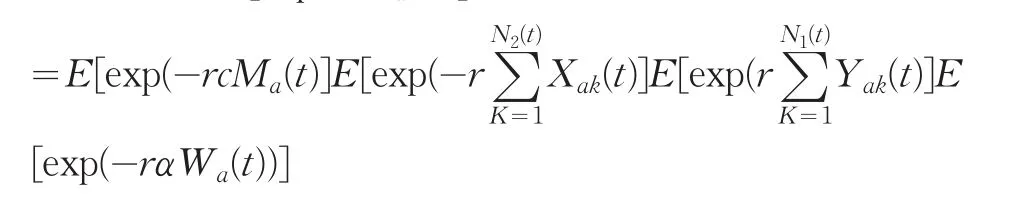
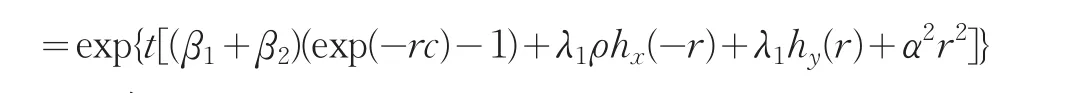
令

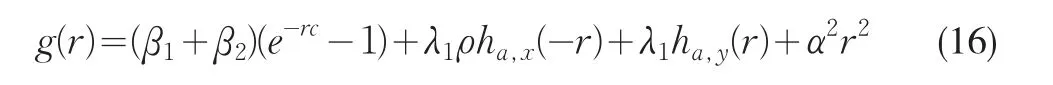
即可。

定理3方程g(r)=0在r＞0內有唯一正解Ra，Ra稱為模型(14)的調節系數，而g(r)=0稱為調節系數方程。

證明：只需證明g(r)具有以下4條性質即可。

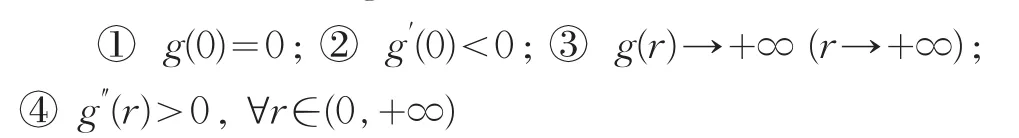
顯然g(0)=0，則①式成立。

由于

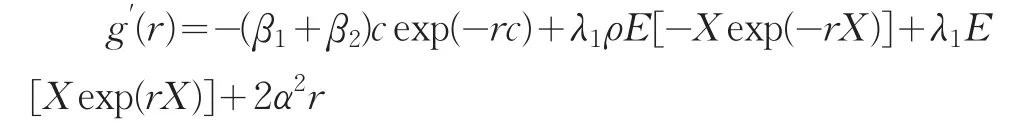
則g′(0)＜0，而

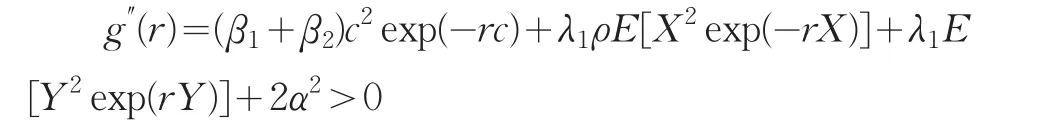
故g(r)在r的非負半軸上是下凸函數，所以g(r)=0至多有兩個解，而r=0為平凡解，故r＞0內有唯一正解r=Ra。

定理4設Ra為調節系數，A為X和Y的上界，則調節系數Ra滿足如下不等式

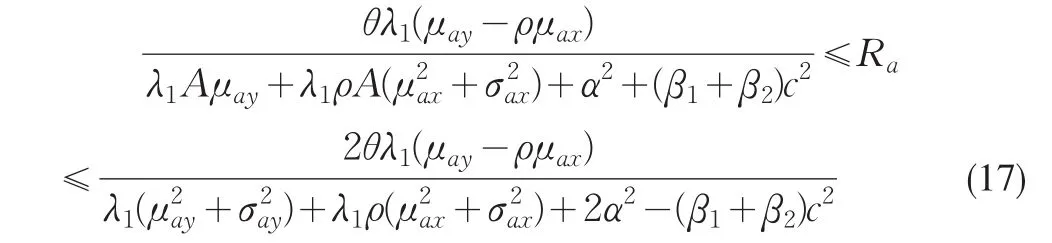
證明方法類似文獻[10]。

對于盈利過程{Sa(t),t≥0}，定義=σ{Sa(v);v≤t}為{Sa(t),t≥0}的自然σ-域流。

定理5Ta是的停時。

定理6{Mˉa(t),t≥0}是鞅，其中：

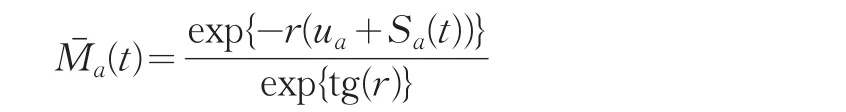
定理7對于任意實數r，其最終破產概率滿足：

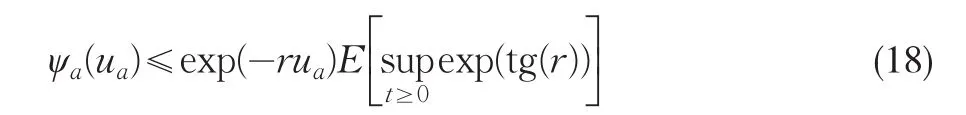
證明：對任意固定常數t0，t0∧Ta為有界停時，從而由鞅的停時定理可得：

所以

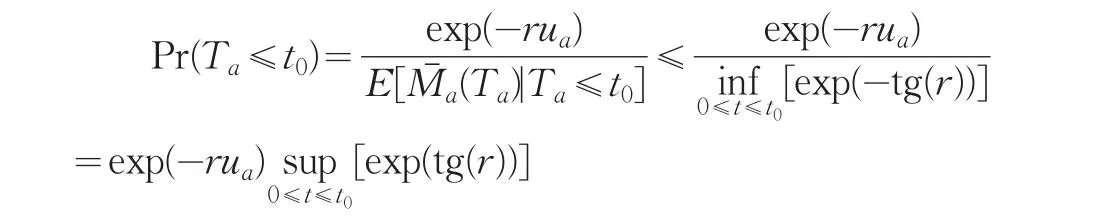
對上式兩邊取期望并令t0→∞，則可得(18)式。

定理8盈余過程{Ua(t);t≥0}的最終破產概率滿足：

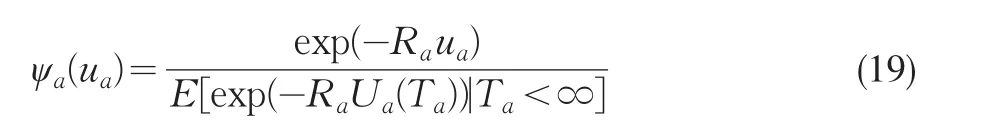
證明對任意的固定常數t0，t0∧Ta為有界停時，從而由有界停時定理可得：

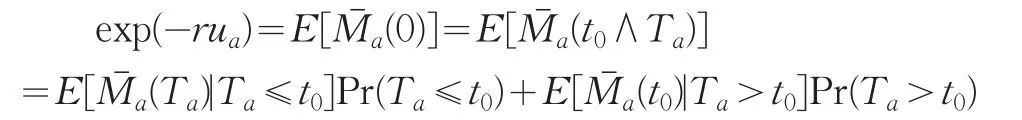
在上式中，取r=Ra得：

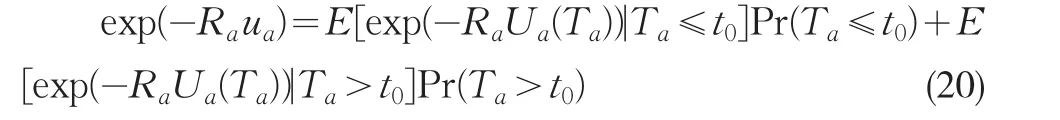
若令I(C)表示集合C的示性函數，則有：

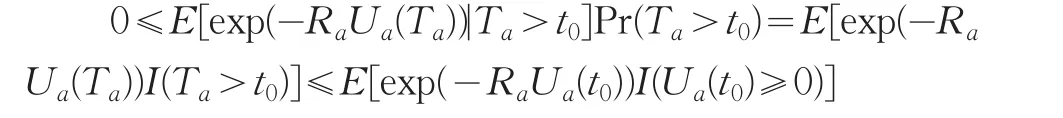
由于0≤exp(-RaUa(t0))I(Ua(t0)≥0)≤1，根據大數定理可證明當t0→∞時，Ua(t0)→∞(幾乎處處)，由控制收斂定理有(幾乎處處)，從而當t0→∞時，式(20)即可化為(19)式。

推論1{Ua(t);t≥0}的最終破產概率所滿足的Lundberg不等式為：

其中，Ra為調節系數。

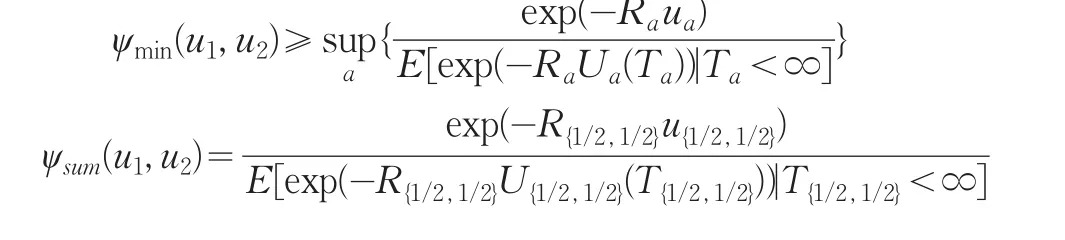
[1]Grande J.Aspect of Risk Theory[M].New York:Spring-Verlag,1991.

[2]Gerber H U.數學風險論導引[M].成世學,嚴穎譯.北京:世界圖書出版發行公司,1997.

[3]Chan Wai-Sum,Yang Hailiang,Zhang Lianzeng.Some Results on Ruin Probabilities in A Two-dimensional Risk Model[J].Insurance: Mathematics and Economics,2003,(32).

[4]Cai J,Li H J.Multivariate Risk Model of Phase Type[J].Insurance: Mathematics and Economics,2005,(36).

[5]馬學思,劉次華.雙Poisson二維風險模型的破產概率[J].統計與決策,2006,(8).

[6]陶金瑞,張永珍,劉俊先.二維相依泊松風險模型的破產概率[J].南開大學學報(自然科學版),2009,42(4).

[7]李祥發,宋會杰,郭鵬江.擾動的二維風險模型的破產概率[J].西北大學學報(自然科學版),2009,38(6).

[8]顏榮芳，潘歡.重尾環境下二維風險模型在有限時間內的破產概率[J].蘭州大學學報(自然科學版),2008,44(2).

[9]楊恒,黎鎖平.改進后的二維相關風險模型[J].甘肅科學學報, 2010,22(1).

[10]于文廣,黃玉娟.隨機利率因素下的多險種破產模型[J].臨沂師范學院學報,2006,28(6).