數形結合剖析水波的干涉圖樣

陳 敏

(慈溪市滸山中學 浙江 寧波 315300)

“波的干涉”一節的教學難點在于對穩定而動態的波的干涉圖樣的理解.穩定性是指空間內每個質點的振動強弱是固定的，動態性則是指每個質點的位移又是時刻變化的.學生感覺比較難以把握的是，穩定和動態的特征表現在干涉圖樣上是怎樣的？畫面動態有序的背后隱含質點遵循著怎樣的規律？通過數形結合的方法來突破上述難點可以取得較為理想的效果.數形結合把直觀的圖形表達方式與抽象的數學表達方式相結合來解決問題，一方面借助數學的精確性和嚴密性對圖形做精細的分析，從而對圖形有更深刻的認識；另一方面用圖像形象地體現數學的抽象表達，有助于對復雜數學公式的理解，達到理解水波干涉圖樣的目標，分析如下.

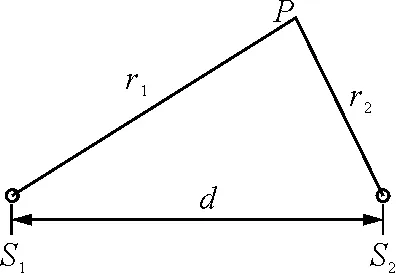
圖1

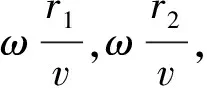
根據波的疊加原理，實際振動的運動學方程為

令

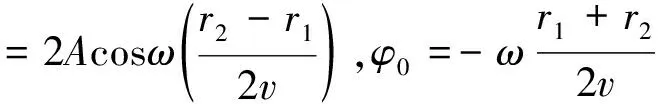
則

y=A合cos(ωt+φ0)

式中A合和φ0分別為兩分振動在P點的合振幅和初相位.可見質點是做角頻率依然為ω的簡諧運動，其振動特征與空間位置和時間變化相關.下面從空間、時間來分析波的干涉圖樣的穩定性和動態性.

1 空間位置決定振幅和初相體現穩定性

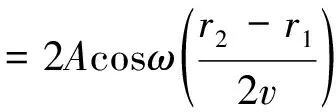
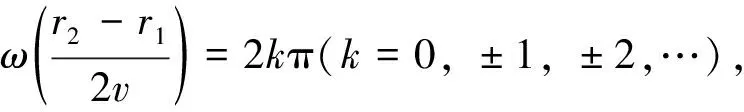
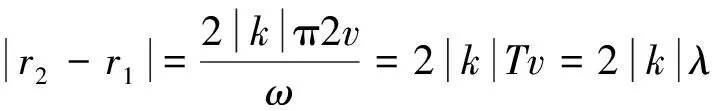
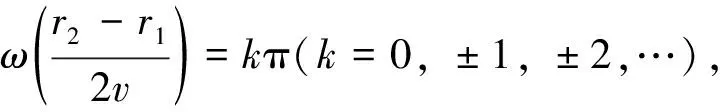
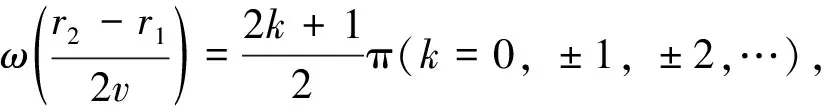
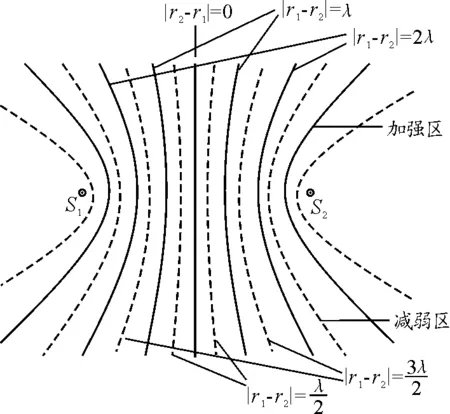
圖2

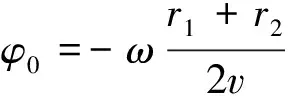
即r1+r2=d+2kλ，質點與S1，S2連線間的質點相差為零，振動步調一致，如圖3實線橢圓.

r1+r2=d+(2k-1)λ

質點與S1，S2連線間的質點振動步調相反，如圖3虛線橢圓.

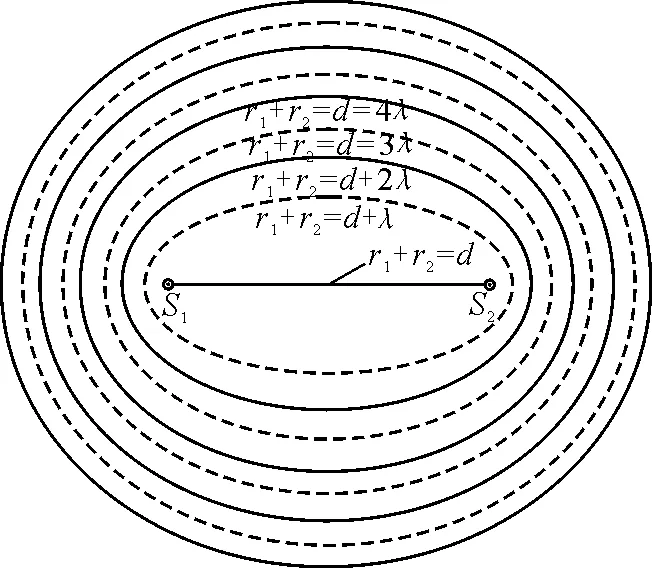
圖3

在單一波源形成波的傳播過程中，每個質點都重復波源的振動形式，相同相位的質點形成的波面是以波源為圓心的一系列同心圓，波面沿半徑方向向外擴散；與此相似，質點在兩個波源的帶動下產生的振動也將從S1，S2連線沿著雙曲線(在S1，S2連線方向上沿連線方向)向外傳播形成越來越大的“同焦”橢圓形的波面，此處的雙曲線和橢圓可類比成波線和波面，如圖4所示.

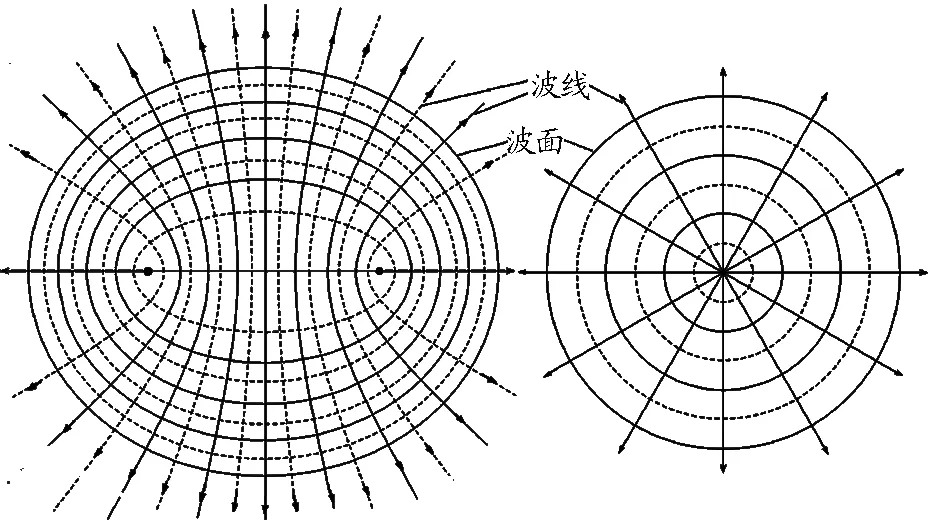
圖4

2 時間決定質點的位移體現動態性

由于有兩個波源使得質點的振動形式較單一波源作用時有更豐富的形式，下面詳細分析兩個波源S1，S2之間的質點的振動，其他質點都可以看作是重復著這些質點的振動形式.

S1，S2連線上的質點的振動方程均可表示成

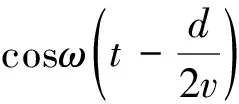
若連線間距為2λ，由

可知，連線的中點A0滿足|r2-r1|=0，是加強點，稱作零級加強區；A1左，A1右滿足|r2-r1|=λ,稱1級加強區；A2左，A2右滿足|r2-r1|=2λ，稱2級加強區.A0，A2左，A2右的振動方程為

A1左，A1右振動方程為

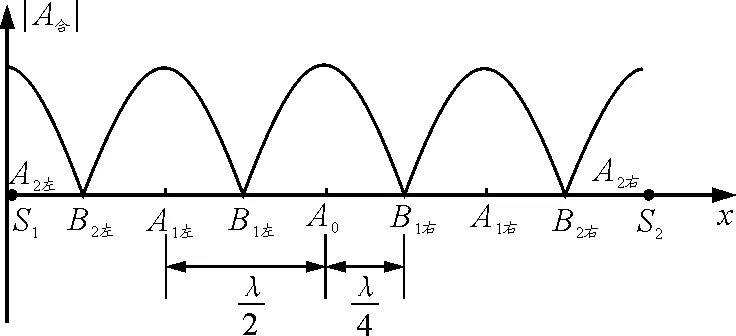
圖5

現在用圖6來說明S1，S2連線上的質點一個周期內所表現出來的波形.圖中可以看到，所有質點在同一時刻到達最大位移，同一時刻經過平衡位置，同一時刻到達最小位移，波形圖并不沿著S1，S2連線方向移動，只看到波形上下起伏.這種由振幅相同傳播方向相反的兩列簡諧相干波疊加得到的振動稱為駐波，相鄰加強區的正負最大位移間隔出現，加強點的起伏最大，形成波腹，減弱點不發生振動，形成波節.駐波不是波而是一種特殊的振動狀態，波源S1，S2連線上質點的振動形式沒有沿著連線傳播，卻沿著雙曲線向外傳播，看起來連線間的振動形式從S1，S2連線出發沿著雙曲線兩側傳播，單一波源形成的波面是一圈圈的同心圓，在水面上看到圓形的漣漪，這里形成的是一圈圈橢圓狀的“波面”，水面上呈現出橢圓狀的漣漪；而且，橢圓上也形成類似的“駐波”，此“駐波”也并不沿著橢圓方向傳播，而是繼續沿著雙曲線蕩成更大的橢圓狀的漣漪.

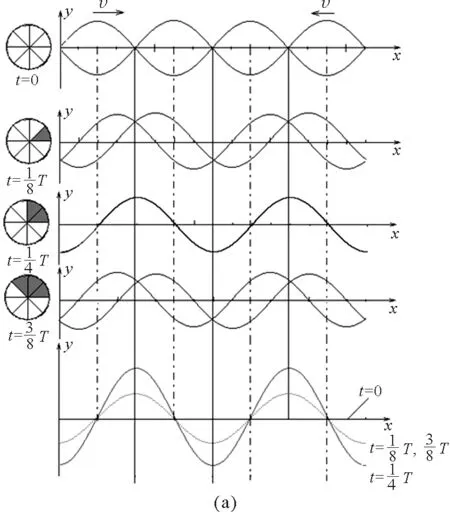
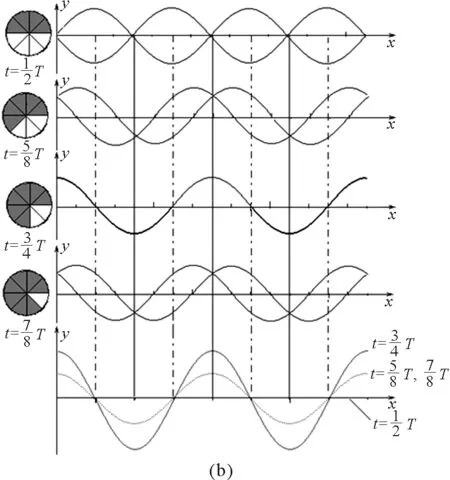
圖6

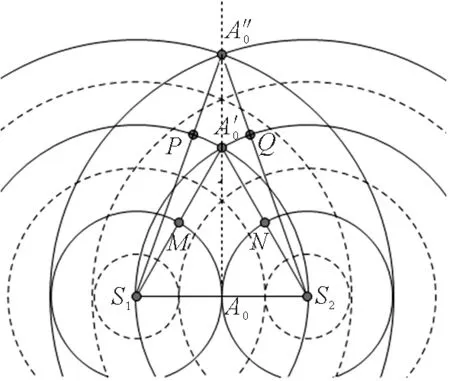
圖7

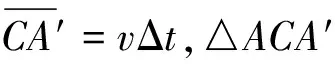
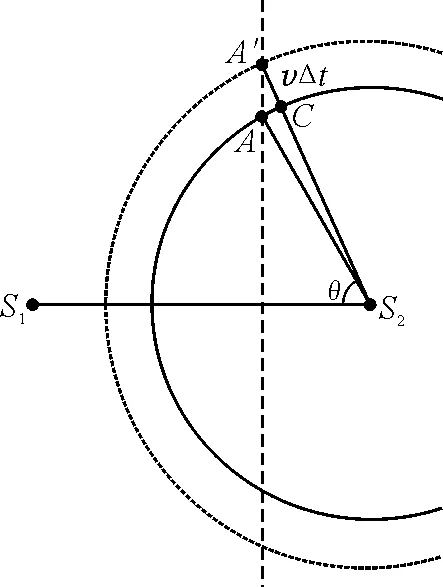
圖8

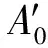
圖9

每一個質點的振動形式是簡單的，但是空間的分布和時間的變化使得整個圖樣錯落有序，變化多端，就像一場大型的團體操表演中，每一個演員的動作并不復雜，但眾多演員的參與，前后左右相鄰演員的動作錯落有致，就形成了氣勢恢宏，蔚為壯觀的藝術畫卷.在干涉現象中，每一個質點嚴格恪守著運動規律，就像是一個個優秀的演員在高度的組織協調下表演，演繹成一幅整齊生動的干涉畫面.