一種NTC熱敏電阻校正方程的試驗研究*

張鵬超，張 強

(1．陜西理工學院電氣工程學院，陜西漢中723000;2．陜西理工學院機械工程學院，陜西 漢 中723000)

NTC熱敏電阻器以其靈敏度高、熱慣性小、受磁場影響小、抗輻射，價格低廉等優點，在實際工作中把NTC熱敏電阻作為溫度傳感器是最為常見的。對提高NTC熱敏電阻的校正方程精度的研究取得了很大的進展。從NTC制造工藝角度提高NTC熱敏電阻測溫的穩定性［1－2］，此方法可以保證NTC熱敏電阻工作的可靠性，但是實際應用中必須對其阻溫特性進行校正，常用的方法有:(1)對NTC熱敏電阻進行的線性化的研究方法［3－4］，此方法誤差較大，且過程復雜;(2)利用傳統的經驗指數校正方程進行分段多項式擬合非線性補償的方法［5］，這種方法需要擬合出多個關系式，一旦超出擬合溫度范圍，精度不能保證，并且應用起來較復雜;(3)采用Steinhart-Hart方程［6－10］對 NTC 熱敏電阻的 R－T 特性進行校正，但是此方法需要擬合4次，且精度不能滿足高精度要求。

近年來，隨著對NTC熱敏電阻的測溫原理研究的深入［11］，采用硬件補償法的研究也廣泛的應用起來［12］，在較小的溫度范圍內能夠得到較高的精度補償效果，但是超出此范圍的測溫精度較差且設計電路復雜，在實際應用中并不可靠;

本文在對傳統的NTC指數校正方程的基礎上，采用線性化變換，利用最小二乘法對實測的R－T數據進行一次、二次、三次、四次擬合，而且此方法擬合出的校正方程結構簡單，并且經過誤差分析和實際應用中驗證了此方法能達到更高的精度。

1 數據的標定

根據實際測溫需要，對NTC熱敏電阻溫度計在273．15 K ～373．15 K(0～100 ℃)采用恒溫水箱控制溫度，用安捷倫表來測量NTC熱敏電阻隨著溫度的變化而對應的電阻值，并且用量程0～100℃的水銀溫度計來測量實際溫度，測得的實際數據見圖1。

圖1 10K熱敏電阻溫度計R－T的實測數據關系曲線

由圖1可以看出NTC熱敏電阻具有高度的非線性特性，且呈現出指數關系，由此引出傳統的NTC熱敏電阻校正方程:

式中:RT是當溫度為T時的電阻值，RT0是當溫度為T0時的電阻值，B是電阻熱敏常數。方程(1)可以進行數據線性化變換［13］以方便擬合，轉換后的表達式為:

式中:a、b為常數，設R=lnRt，式(3)可以看成T=a+b·R，由此可以看出NTC熱敏電阻的R－T特性關系為一次函數關系;本文將應用最小二乘法來對式(3)分別進行一次，二次，三次，四次擬合，再利用誤差評價原理評價出最適合NTC熱敏電阻的校正方程。

2 基于Matlab的數據擬合方法

2．1 最小二乘法擬合的基本思想［13］

本文基于Matlab運用最小二乘法來對實測數據進行擬合:即選擇一個多項式p(x)，使平方誤差(在某種意義下)達到極小的方式來逼近一個已知函數，其基本思想首先為Gauss所提出，有幾種版本，取決于所涉及的自變量的集合及所用的誤差度量。

首先，當數據為離散時，我們可以對給定的數據xi，yi及 m＜N 將和

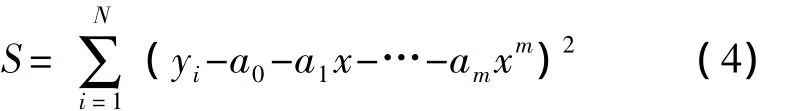
極小化，條件m＜N使多項式

式(5)未必能在所有N個數據點上都能匹配，故S很可能不會變成零。高斯思想是盡我們所能使S變小。經過多年得研究發展，得到了最小二乘法的另一種形式，即:

含有新系數ak，決定這些ak的方程組證明特別容易求解:

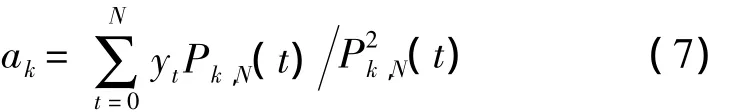
這些ak的確使誤差和S極小化，極小值為

其中Wk為表達式中作為分母的和式，擬合后的方程系數如表1所示。

表1 10K熱敏電阻擬合關系式系數

2．2 Matlab 實現

應用Matlab工具箱的Polyfit(R，T，n)對NTC熱敏電阻的R－T特性分別進行一次，二次，三次，四次擬合或者更高次的擬合，R為lnRT值、T為實測溫度值、n為最小二乘擬合次數。擬合后的方程系數已由表1所示。

2．3 誤差評價原理［14］

由于本文所選用的都是經驗公式，在擬合過程中對有效數字的選取，導致了試驗誤差的存在，盡管標定中R、T都有4位有效數字，但是必然存在試驗的測量誤差。所以測量值f與擬合值之間要滿足下面的關系:

可以利用絕對誤差、平均誤差以及均方根誤差來比較擬合曲線與實測數據之間的誤差。

2．3．1 絕對誤差:

式中:E(f)為各個校正方程的絕對誤差;yk是各個關系式的擬合值;f(xk)絕對誤差變化得越平穩，證明方程的精度越高。

2．3．2 平均誤差:

式中:E1(f)為校正方程擬合的平均誤差;N為實測數據點數;式中的意義是擬合后的平均誤差的絕對值求和后再求平均值，E1(f)越小，表示方程的精度越高。

2．3．3 方程有效性的評價

一組近似值Ai對相應的真值Ti的標準差定義為［14］:

E2(f)為校正方程的標準差;在Ti為已知的各種試驗情況下，我們將用這個誤差度量來估計最小二乘平滑化的有效性;E2(f)越小，表示方程精度越高。

2．4 評價校正方程:

通過表1的各個擬合方程的系數進行誤差分析，由圖2可以看出對NTC熱敏電阻的R－T特性關系進行一次擬合的誤差震蕩比較大，對于二次，三次，四次擬合誤差，不太好評價好壞，因此，對此3種擬合的平均誤差及標準差進行對比，以便評價出更適合NTC熱敏電阻的校正方程，見表2。

圖2 四種擬合絕對誤差對比

表2 10K熱敏電阻4個方程擬合誤差

表2中E1(f)/K為平均誤差，E2(f)/K為評價方程有效性的標準差。根據誤差評價原則:分別去掉一個最大誤差、最小誤差。由表2可以看出:四次擬合方程的E1(f)/K=0．286 3及E2(f)/K=0．412 8最小，可以看出，經過四次擬合的方程在237．15 K～337．15 K(0～100℃)范圍內是最適合NTC熱敏電阻溫度計精度的校正方程。

3 結論

通過對傳統的指數方程進行線性變換，得到一種新的NTC熱敏電阻溫度計R－T特性關系，對此關系進行最小二乘擬合，并進行了絕對誤差，最大、最小絕對誤差，平均誤差的分析之后，可以看出，對于式(3)進行一次擬合得到的方程不能精確地對NTC熱敏電阻溫度計的非線性進行校正;通過對NTC熱敏電阻溫度計的R－T特性關系進行更高階的擬合并求出各個擬合方程的標準差，比較之后得出四次最小二乘擬合的方程是最適合NTC熱敏電阻溫度計的校正方程，適用于NTC熱敏電阻的具體校正方程如下:

實際上，由表2可以看出，對NTC熱敏電阻的R－T實測數據應用最小二乘法，進行二次擬合得出的校正方程的精度已經比傳統的校正方程高很多，可根據具體工況來決定選擇校正方程。應用式(13)在實際的應用當中得到了很好的驗證，保證精度，且測量方法簡單，價格便宜，宜廣泛應用，本文確定校正方程的方法適用于各類熱敏電阻溫度計的校正擬合。

［1］ 翟繼衛，沈波，妥萬錄，等．熱壓燒結對NTC熱敏電阻穩定性的影響［J］．傳感技術學報，1996，1(4):32－34．

［2］ 武明堂，鄧長霖，李平．(NiCo)(CoFe)系NTC熱敏半導瓷新材料的研究［J］．傳感技術學報，1988，1(2):33－40．

［3］ 趙軍，謝作品，吳珂．NTC熱敏電阻線性化新方法［J］．電測與儀表，2006，43(1):12－14．

［4］ 沙占友，王彥朋，杜之濤．NTC熱敏電阻的線性化及其研究［J］．自動化儀表，2004，25(9):28－30．

［5］ 杜西亮，孫慧明，聶義祥．NTC熱敏電阻器分段多項式擬合非線性補償［J］．傳感器技術，2005，24(8):13－15．

［6］ White D R．Technical Guide10-A Simple，Narrow-Band，Thermistors Themometer［M］．Measurement Standards Laboratory of New Zealand，2005．

［7］ 蘭玉岐，朱曉彤，李山峰，等．低溫用NTC熱敏電阻校準方程的評估［J］．低溫工程，2010(5):50－52．

［8］ SteinhartI S，Hart S R．Calibrationcurves for Thermistors［J］．Deep Sea Research，1968，15(3):497－503．

［9］ Lightwabe I L X．Thermistors Calibration and the Steinhart-Hart E-quation［M］．ILX Lightwate Corporation，2003．

［10］ Alexander M D，Mac Quarre K T B．Toward Standard Thermistor Calibration Method and Data Correction Spreadsheets［J］．Review of Scientific Instrument，1988，59:975－979．

［11］范寒柏，謝漢華．基于NTC熱敏電阻的三種高精度測溫系統研究［J］．傳感技術學報，2010，23(11):1576－1579．

［12］崔文德，李鐵鵬，牛建永，等．熱敏電阻低溫測量方法研究［J］．宇航計測技術，2010，30(4):25－31．

［13］羅亮生，包雪松，王國英．數值分析(全美經典學習指導系列)［M］．科學出版社，2002．

［14］ 周璐，陳渝，錢方，等．數值方法(MATLAB 版)［M］．4版．電子工業出版社，2005．