例談在計算教學中培養學生的創新能力

　　對學生而言，創新能力是反映學生創新水平最現實的表現。枯燥的計算教學能否培養學生的創新能力呢？本文就如何在計算教學中培養學生的創新能力進行了一些嘗試。
　　一、適度猜想，培養想象能力
　　愛因斯坦說過：“想象比知識更重要，因為知識是有限的，而想象可以包羅整個宇宙。”因此，教師在教學中引導學生進行合理猜想，往往能縮短解決問題的時間，獲得數學發現的機會，鍛煉數學思維。
　　如在教學“兩位數加兩位數的口算”時，教師創設了如下的情境。
　　師：兒子過生日那天，帶他去超市買玩具作為生日禮物，他選了兩個機器人（出示場景圖）。我先賣個關子，不告訴你們具體的價格，只告訴這個（出示4□元，3□元），請你猜一猜，買這兩個機器人玩具我可能花了多少錢？
　　生1：可能花了七十多元。
　　生2：我覺得有可能是八十多元。
　　生3：可能是七十元。
　　生4：可能是八十元。
　　師：你能說說什么情況下我只要付七十多元，而什么情況下我要付八十多元呢？（學生一聽，情緒高漲，思維更加積極）
　　生5：如果個位相加不滿十，就只要付七十多元，因為個位不滿十，十位上4加3等于7，就是七十多元。
　　生6：個位相加要是滿十，就要付八十多元，因為十位4加3還要加進上的1就是八十多元。
　　生7：個位上都是0，就只要付70元。
　　生8：個位上都是5，35+45等于80，就正好是付80元。
　　……
　　師：我有沒有可能付九十幾元，或者一百多元呢？
　　生9：不行，最多只要付八十幾元，因為如果方框里填最大的數9，那么49+39等于88元，最多也只要付88元，不可能付九十多元，更不可能付一百多元……
　　教師創設了一個過生日買東西的情境，并且故意賣個關子不告訴學生具體的價錢，從而激起學生猜想的熱情。這一猜測是學生通過思考完全能夠解決的，既是對舊知的復習，更是對估算、計算的綜合應用。這樣創設興趣情境，造成懸念，讓學生猜想，啟動了學生思維的閘門，使學生愉快地、不知不覺地進入探求知識的活動之中。呈現方式的改變，具有現實意義的猜想，猶如一股春風，無疑使原本單調的計算課變得鮮活起來，枯燥的數學課堂也因此變得讓學生有所期待。
　　二、引導遷移，培養聯想能力
　　創造力有賴于聯想，聯想能力有引導作用。教學中，教師應根據教材潛在的因素，創設情境，提供材料，引導遷移，誘發學生的創造性聯想。
　　如“兩位數加兩位數的口算”的教學，普遍感覺學生的思維單一，計算方法基本只有一種，即采用個位加個位、十位加十位的筆算式口算。究其原因是在之前已經學過兩位數加兩位數的筆算，在學生頭腦里已先入為主，且根深蒂固。如何幫助學生進行適當反思，提升對相關口算方法的理解水平？在教學中，我作了適度引導，當計算43+32，學生的方法呈現單一時，我指出：“看來這一方法挺適合你們的，不過，我這里還有一種方法想要介紹，希望能給大家以新的啟示。我把其中一個數拆成一個整十數和一個一位數，根據以前學的知識，你猜猜，我可能先算什么？”
　　生1：先算32+40=72，再算72+3=75。
　　生2：先算32+3=35，再算35+40=75。
　　生3：也可以把32拆成30和2，先算43+30=73，再算73+2=75。
　　生4：先算43+2=45，再算45+30=75。
　　……
　　算法多樣化的目的就是為了讓學生開拓思路、拓展思維，體悟計算方法的多樣性。當學生實在想不出的時候，怎么辦？避而不講不符合教材的要求，直接告知也限制了學生思維的發展。因此，在教學中當學生呈現方法單一的時候，我指出：“我這里還有一種方法想要介紹，希望能給大家以新的啟示。我把其中一個數拆成一個整十數和一個一位數，根據以前學的知識，你猜猜，我可能先算什么？”通過引導、交流、分享，學生將舊知遷移，聯想出了多種解答方法，不僅在口算方法上建立合理的認知，更達到了思維的共享。
　　三、注重比較，培養觀察能力
　　創造力來自敏銳的觀察，觀察能力起奠基作用。達爾文說過：“我既沒有突出的理解力，也沒有過人的機智，只是在覺察那些稍縱即逝的事件，并對其進行精細觀察的能力上，我可能在眾人之上。”由此可見，凡科學上的重大發明，都由于善于觀察。
　　如在“兩位數加兩位數的口算”的教學中，有以下四組練習題：
　　26+352+8 37+519+6
　　26+4352+1837+2519+36
　　26+6352+3837+5519+76
　　教師首先出示第一組算式，并用神秘的語氣對學生說：“老師這里有一組很特別的題目，仔細觀察一下，你有什么發現嗎？”
　　生1：第一個加數都是26。
　　生2：第二個加數個位上都是3。
　　生3：第二個加數一個比一個大。
　　師：這么特別的算式，你會算嗎？（學生嘗試計算，然后匯報交流）
　　師：通過剛才的計算，你有什么發現嗎？
　　生4：和一個比一個大。
　　生5：第二個和比第一個和多40。
　　師：為什么會多40，與加數有什么聯系嗎？
　　生6：第二題的第二個加數比第一題的第二個加數多40，所以和也多40。
　　生7：和的個位都是9。
　　師：和的個位為什么都是9呢？
　　生8：因為加數的個位都是6和3。
　　生9：我發現每題都可以先算26+3=29，然后第2題就在29的基礎上加40就是69，第三題就在29的基礎上加60，就是89。（學生們不由得鼓起掌來……）
　　以案例中的這組習題為例，假如僅僅作為口算題來處理，那學生就只是做了幾道口算題而已，對于思維的發展和提升來說，沒有任何作用。因此，教師在設計的時候，先讓學生觀察其中的一組，讓學生通過觀察、比較，發現式子間的聯系和區別。計算后教師繼續讓學生觀察：“計算時有什么發現？”通過兩次對比思考，學生很好地把握了題與題之間的聯系，進一步領會了計算方法上的特點，從而更深刻地掌握了兩位數加兩位數的口算方法。學生正是因為有了細致的觀察為基礎，才會有如此深刻的發現。
　　四、合理估測，培養推理能力
　　創造力離不開推理能力，推理能力將創造力推向高潮。估算是運用知識合理推算的過程，是發展數學思維的載體。通過合情推理和演繹推理來發展數學思維，有利于培養思維的靈活性和深刻性。
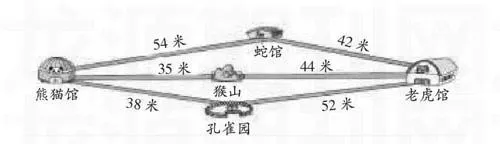
　　如教學“兩位數加兩位數的口算”中，設計這樣一道題：
　　師：不計算，你知道熊貓館到老虎館走哪條路最近嗎？
　　生1：經過猴山的路最近，因為它是直的。
　　生2：往蛇館走大約90多米，往猴山走大約70多米，往孔雀園走是90米，所以往猴山走近。
　　師：小明和小紅游完猴山后，一個想去蛇館，一個想去孔雀園，意見不一，怎么辦呢？最后決定哪個館離猴山近，他們就去哪個館玩，猜一猜，他們去哪個館玩了？說出理由。
　　（學生同桌討論后，一致認為是先去了孔雀園，因為往孔雀園最近的路只要70多米，而往蛇館最近的路要80多米）
　　……
　　估測有利于培養學生的直觀判斷能力和簡單推理能力。許多數學問題，包括世界名題的解決，都是首先從圖形或數據的直接觀察中獲得某種直覺猜想，然后再進行邏輯證明的。在教學中，教師要注重對學生估算意識和能力的培養，從而發展學生的推理能力。
　　創新能力不是單一的能力，是以思維的主動性、新穎性、深刻性和高度概括性為主要表現的。課堂上，教師要盡量創造合適的條件，努力培養學生的創新能力。
　　（責編杜華）