有效拓展學生解答應用題思維的探索

　　 教師在教學過程中不僅要教學生“學會”，而且要教學生“會學”“善學”，這是課程改革對每一位教師提出的新要求。因此，激發學生思維動機，理清學生思維脈絡，教給學生思維方法，是有效拓展學生解答應用題思維的關鍵所在。下面，本人圍繞“有效拓展學生解答應用題思維”問題談幾條策略，與大家交流探討。
　　一、一題多說
　　多說解題思維過程能促進學生邏輯思維條理性的形成，同時對培養分析、推理、概括等能力起促進作用。說的過程是深入理解知識的過程，也是集思廣益、互幫互學的過程。說的形式可運用執因索果法（綜合法——從條件到問題），也可以運用執果索因法（分析法——從問題到條件）。如：一個表面積是412平方米的長方體紙箱，把它放在地上至少占地44平方分米，這時底面周長是27分米。則其體積是多少立方分米？可以這樣引導學生說：（1）根據“長方體的體積=底面積×高”或“長方體的體積=長×寬×高”可知，要求長方體的體積必須知道“長、寬、高”或“底面積和高”，題中已提供“長方體的底面積”（占地44平方分米），還缺“高”，因此，可以把求“長方體的體積”問題轉化為求“長方體的高”問題。（2）已知長方體的表面積412平方分米和底面積44平方分米，可求出長方體的側面積（412-44×2=324平方分米）；已知長方體的側面積324平方分米和底面周長27分米（把長方體的側面展開，可知底面周長就是長方形的長），可求出長方體的高（324÷27=12分米）。這樣，中間問題被解決了，長方體的體積也就迎刃而解了。為了提高數學語言表達能力和解題能力，引導學生說思維分析過程之前，可以嘗試要求學生把思維分析過程用“文字結合符號”表達出來，還可以嘗試要求學生寫出解題計劃。
　　二、一題多變
　　加強“一題多變”的思維訓練，既是提高學生審題能力的重要途徑，又是培養學生解題思維深刻性、靈活性的重要策略。如教學求圓柱體總面積時，為了提高學生解題思維的辨別能力，可以設計一道有“替換”的條件的題目：“一個圓柱形化糞池，底面直徑2米（底面半徑1米或底面周長6．28米），深3米，若在池的周圍與底面抹一層水泥（在池的周圍抹一層水泥或在池的周圍、底面與頂面抹一層水泥），抹水泥部分的面積是多少？”啟發學生細讀括號中的詞或數據，并與原字詞或數據相比較，從中領悟重點詞或數據的內涵，掌握解題策略。即：①有蓋有底的總面積（表面積）=側面積+底面積×2；②無蓋有底的總面積=側面積+底面積；③無蓋無底的總面積（側面積）=底面周長×高。若常用這種“變條件”的訓練思維形式，則能培養學生對“條件與問題”對應的判斷習慣，有效拓寬了解題思路，從而提高解題的技巧和能力。
　　三、一題多問
　　加強應用題“一題多問”的訓練，不但對學生把握應用題的結構和深刻理解數量關系有著重要的教學價值，而且讓學生在提出問題與解決問題的過程中充分展現教師開放式教學策略和有效培養學生問題意識、創新意識和解決問題能力。如：教學分數或百分數應用題時，為了提高學生找“量與率”或“問題與率”對應關系的能力，可以設計一道能提出開放性問題的題目讓學生訓練：“一包洗衣粉重300克，第一次用去1／6，第二次用去1／10。問題：①還剩下多少千克？②第一次、第二次各用多少千克？③第一次比第二次多用多少千克？④第二次比第一次少用多少千克？⑤兩次共用去多少千克？⑥剩下的比用去的多多少千克？⑦用去的少多少千克？……通過借助“畫線段圖”工具，學生直觀、準確地找出了“問題與分率”的對應關系：剩下的洗衣粉重量占一包洗衣粉的（1-1／6-1／10）；兩次共用去的占一包洗衣粉的（1／6+1／10）；第二次比第一次少用的占一包洗衣粉的（1／6-1／10）；第一次比第二次多用的占一包洗衣粉的（1／6-1／10）……從而對所提的問題一一破解。這樣，通過多角度進行思考和探索，提升了數學訓練功能，培養了提出問題、解決問題的能力。
　　四、一題多解
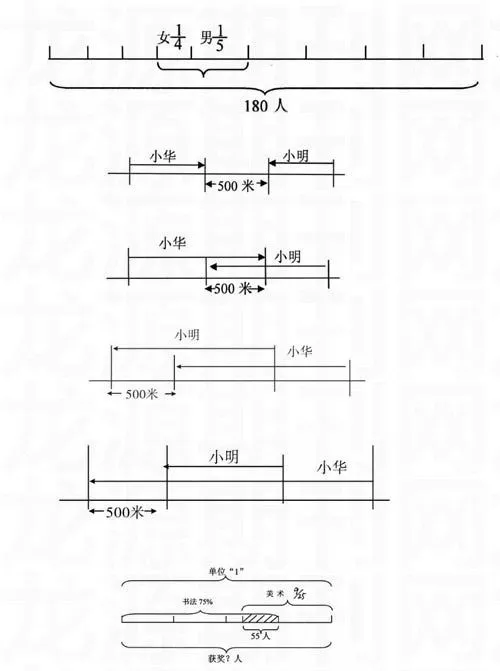
　　大家常講的所謂“一題多解”，正是指從數學知識的各種不同角度，運用不同的思維方法去解決同一個問題。常使用這種策略，能激活學生的解題思維、養成多角度解決問題的習慣，從而培養學生思維的多向性、靈活性。一題多解（算法多樣化）的拓展途徑：答案唯一型和答案不唯一型。（1）答案唯一型訓練。如：某市中醫院有醫生180人，市政府從該中醫院抽走了1／4的女醫生和1／5的男醫生去四川抗震救災，現在該中醫院還剩下139人。這個中醫院有男、女醫生各多少人？解答時，可以引導學生采用算術法解答。通過借助畫線段圖：
　　不難找出已知數與分率相對應。假如以男醫生人數為“1”，[180-（180-139）×4]=16（人）與1/5相對應，則算術式：[180-（180-139）×4]÷1/5，可解得男醫生80人，女醫生100人;假如以女醫生人數為“1”，[（180-139）×5-180]=25（人）與1/4相對應，則由算式：[（180-139）×5-180]÷