走出《空間與圖形》教學的誤區

　　近幾年，筆者聽了有關《空間與圖形》的一些課，測試題的反饋情況，暴露了部分教師在教學這一內容時存在著一些共性問題。現從中摘取幾個案例來分析。
　　
　　一、重視死記公式，忽視意義引領
　　
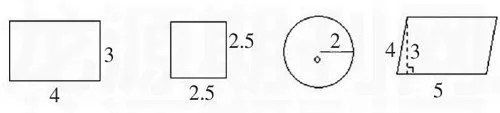
　　［案例1］求下列圖形的周長。(單位：厘米)
　　求長方形、正方形、圓的周長時，學生根據周長公式，很快就解答出來了。
　　師：現在請同學們求平行四邊形的周長，誰來說說？
　　生1：(5+3)×2=16(厘米)。
　　師：說說你的理由。
　　生1：根據長方形的周長公式來求。
　　師：有不同意見嗎？(大多數學生搖搖頭，表示沒有意見)
　　生2：老師，我們沒有學過求平行四邊形的周長公式，解不出來。
　　生3：老師，我覺得應該這樣列式，不知道對不對？(5+4)×2=18(厘米)。
　　………
　　［反思］
　　案例中學生求長方形、正方形、圓的周長時是那樣得輕車熟路，而在求平行四邊形的周長時卻是表現不一：有的猶豫不決，不敢下筆；有的套用長方形周長的計算公式；有的說沒有學過求平行四邊形的周長公式，解答不出來；有的對自己正確的解法不敢肯定……這折射出了在平時的教學中相當一部分老師只強調學生記住公式，忽視了周長的意義建構。有的學生甚至不知道周長指的是什么，腦海中根本沒有“周長”的空間意義和相應的表象。解題時只是條件反射地機械地套用現成公式，離開了公式就無從下手，猶如盲人沒有了拐杖，寸步難行。這樣的教學，打造出來的學生只會模仿，不會變通，更談不上創新。基于此，教學中一定要讓學生參與公式的建構過程，讓學生在理解意義的基礎上建構公式，唯有這樣，公式才是活的，才是有用的，才會觸類旁通，舉一反三。其實，學生一旦領悟了周長的意義，計算這些平面圖形的周長(圓除外)，根本就不需要公式，只要根據周長的意義就可以計算了。因此，有了意義的引領，即使沒有公式，心中自有公式；沒有意義的引領，死記公式，公式也將成為無源之水，無本之木。
　　
　　二、重視常規解法，忽視創新解法
　　
　　［案例2］學習圓柱的表面積時，絕大部分教師僅僅滿足于課本中的常規解法。一旦引導學生得出圓柱的表面積等于側面積加上兩底面積的和，教學馬上就此打住，覺得大功告成，而對求圓柱表面積的創新方法S表=C×（h+r）只字不提。
　　［反思］
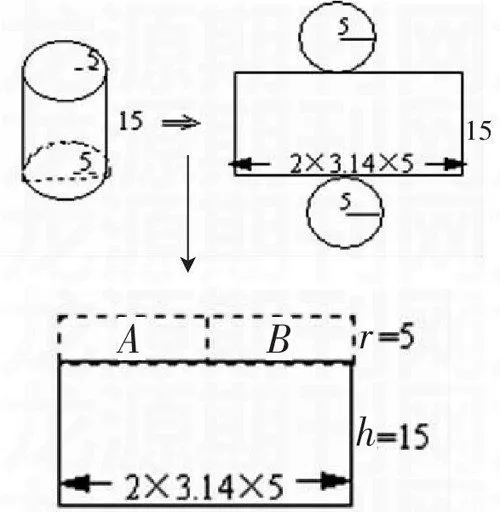
　　這本應該成為這堂課中培養學生創新能力的“生花之筆”，掀起這堂課的高潮，點燃學生的創新之火，可惜絕大多數教師都沒有好好利用，錯失良機。為什么會出現這種現象呢？筆者認為有兩種情況：其一，有的教師沒有吃透教材，根本就不知道圓柱的表面積還可以這樣求；其二，有的教師唯課本方法至上，教學僅停留在復制例題上。這種只局限于書本的知識與思路，局限于舊的想法與方法，不去創造性地處理教材，不能創造性地教學，不能從多方面、多角度開拓學生思維的教學，塑造出的學生只會墨守成規，循規蹈矩，不敢越雷池半步。如上例引導學生得出課本的解法后，只要稍作啟發，我們已經學過圓可以轉化為長方形，求圓柱的表面積除了這種方法外，同學們想一想還可以怎樣計算？學生有了圓面積的推導經驗，就不難得出圓柱表面積的另一種求法：將圓柱的上、下兩個底面分別轉化成兩個長方形A和B（見下圖），再與圓柱側面展開的長方形拼成一個新的長方形。這樣求圓柱的表面積就轉化成求一個長方形的面積，長方形的長等于圓柱的底面周長，長方形的寬等于圓柱的高加上圓柱的底面半徑，即圓柱的表面積等于底面周長乘以高與半徑的和，用字母表示S表=C×（h+r）。讓學生用這種方法計算例題，再與上述方法對比，體驗本方法的優越性。在此基礎上，引導學生探究無蓋圓柱表面積的方法已是呼之即出，即S表（無蓋）=C×（h+r÷2）。添加這一筆，充分挖掘了例題的開放價值，學生求圓柱的表面積不再囿于一種固定的方法，體現了解決問題策略的多樣化，符合新課標理念。
　　例題解法一：2×3.14×5×15+3.14×52×2=628（cm2）。
　　創新解法二：2×3.14×5×（5+15）=628（cm2）。
　　
　　三、重視透路解題 忽視思路變通
　　
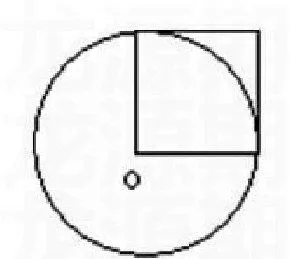
　　［案例3］下圖中正方形的面積是20cm2。
　　求圓的面積。
　　生1：老師，哪兩個一樣的數相乘等于20？
　　生2：老師，數據出錯了，將20cm2改為25cm2，我們就會求了。
　　生3：對了，我認為也是這樣，還可以將20改為36、49、81、64、100都可以。
　　生4：老師，我們沒有辦法求出圓的半徑。
　　………
　　［反思］
　　可悲呀！已知r2=20cm2，卻不知如何求圓的面積。為什么求圓的面積只有知道半徑才能求，而知道半徑的平方學生反而不會求了呢？這無不歸功于教師的“精妙之點”：同學們要求圓的面積，必須知道圓的半徑，請記住。殊不知就是這所謂的教師“精妙之點”，已經將學生逼進了思維的“死胡同”，跳不出教師教給他們的求圓的面積必須先求半徑的思路，就像孫猴子永遠都跳不出如來佛的手掌心。這種教學勢必造成學生只會生搬硬套，依葫蘆畫瓢。因此，教學中盡量避免“要求什么，必須知道什么”這樣的套路解題，這無疑給學生造成一種思維定勢，既指明了學生思維的方向，同時也限制了學生思維的方向。一旦思維方向受阻，將不知另辟蹊徑，無法走出“山重水復疑無路”的困境。案例中，學生就是被求圓的面積必須先求出半徑這樣的一種解題套路牽著鼻子走，思維一直鎖定在怎樣求圓的半徑上，而對于小學生來說這是一條死路，是行不通的。如果學生不受制于這種套路解題，在第一次思維受阻后，將會變更思考方向，走出在一棵樹上吊死的困境，迎來“柳暗花明又一村”的新氣象。原來，正方形的面積20cm2就是圓的半徑的平方，求圓的面積直接將3.14×20=62.8（cm2）就好了，根本沒必要求圓的半徑。其實，利用圓的面積占圓外接正方形面積的157／200，也可以求出圓的面積，20×4×157／200=62.8（cm2）。這說明了求圓的面積并不一定非要知道半徑不可。有的教師總喜歡給學生套上框框，堵死了學生的思維，聰明的學生也教傻了；而沒有給學生套框框，思維是活的、變通的，學生越教越聰明。
　　［案例4］
　　1.一個圓柱的側面積是100cm2，底面半徑是2cm。求這個圓柱的體積。
　　從學生的解答情況來看，都是局限于先求出高，再求體積這樣一種思路。絕大多數學生這樣列式，圓柱的高為100÷（2×3.14×2）≈8（cm），體積是3.14×22×8=100.48（cm3）；有的學生因為求高遇到除不盡，就沒有辦法往下求了；有少部分學生運用約分法，避免了除不盡的現象，列式：3.14×22×100／2×3.14×2=100（cm3）。
　　2.把一個底面周長為12.56cm的圓柱體轉化成一個與它等底等高的長方體，表面積多了40cm2。求這個圓柱體的體積。
　　縱觀學生的試卷，能完整地解答出此題的學生不多，都是受制于底面積乘高這一思路。
　　［反思］
　　案例中的第1題其實有更簡便的解答方法：直接用圓柱側面積的一半乘半徑即可。為什么此思路無人問津，學生偏偏要舍近求遠呢？案例中的第2題，為什么多數學生陷入僵局，一些成績優秀的學生也受制于底面積乘高這一思路呢？原因就在于教者在教學圓柱的體積公式時，只重視公式的推導結果，忽視了公式的推導過程，造成學生只知道求圓柱的體積一定要底面積乘高的思路。這種重結論而輕過程的教法直接導致了學生思維的僵化，非常不利于學生的發展。其實，在推導過程中只要引導學生認真觀察、操作，學生是很容易發現圓柱體轉化成與它等底等高的長方體時，表面積變了，多了兩個面，每個面的面積等于半徑乘高。體積不變，由于長方體可以從三個不同的角度擺放，因此推導圓柱的體積公式時也就可以從不同的角度來觀察：⑴當長方體與圓柱體等底等高時，圓柱的體積等于底面積乘高，用字母表示V=sh；⑵當長方體的前面或后面作底面，寬作高時（前面相當于側面積的一半，寬相當于圓柱的半徑），圓柱的體積等于側面積的一半乘半徑，用字母表示為V=S側÷2×r；⑶當長方體的左面或右面作底面，長作高時（左面是多出來的一個面，面積等于半徑乘高，長相當于圓柱的底面周長的一半），圓柱的體積等于半徑乘高再乘底面周長的一半，用字母表示為V=rh×c÷2。學生一旦經歷了這樣的推導過程，不但創造性地掌握了圓柱的體積公式，更重要的是培養了學生的空間觀念、分析能力、邏輯思維能力、概括能力及實踐能力。遇到上述問題，將迎刃而解。案例中第1題圓柱的體積等于100÷2×2=100（cm3），第2題圓柱的體積等于40÷2×（12.56÷2）=125.6（cm3）。同時讓學生體驗了從不同角度思考問題，給解決問題帶來了方便，滲透了在變中尋找不變，不變中尋找變的數學思想方法。
　　
　　四、重視行為、符號把握，忽視圖像把握
　　
　　［案例5］教學長方形面積公式的推導時，一位老師是這樣進行的：
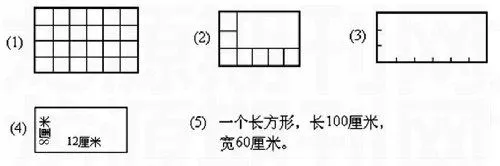
　　⑴擺一擺，數一數。指導學生在長5cm、寬3cm的長方形紙板上，用面積1cm2的正方形擺，數一數一共擺了幾個1平方米；（2）說一說：長方形所含的平方厘米數與長和寬所含厘米數有什么關系？隨即歸納出長方形的面積公式。
　　［反思］
　　布魯納認為：“從形成知識的順序和方式來看，至少有三層階梯：第一層是行為把握，這是依靠動用手足去把握對象；第二層是圖像把握，這是以印象的方式去把握對象；第三層是符號把握，這是以語言形式或數量形式去把握對象的高級階段。”同時又指出：“在教授初學的學習者時，教授工作應這樣處置：使三種‘把握’：行為式→圖像式→符號式，處于最優的協調狀態。這是因為，兒童的發展原則上是經過這三個階段完成的。所以，教授初學的兒童，根據這個順序乃是最優方案。”很顯然，兒童的認知發展必須經過具體形象思維過渡到抽象概括的過程。上述案例，雖然也通過直觀操作讓學生建立表象，但忽視了表象的再現和用表象來思考、想象這一環節，即沒有做好充分的“過渡”工作，造成學生思維的“斷層”，沒有達到布魯納所說的三種“把握”的“最優的協調狀態”。因而所建立的表象還是不夠牢固、不夠清晰的，這就必然影響后續階段的抽象概括。因此，長方形面積公式的推導，應按以下三個階段進行：
　　1.動手操作即行為把握。指導學生在長5厘米、寬3厘米的長方形紙板上，用面積是1平方厘米的正方形來擺，看看沿長擺能擺幾個？沿寬擺能擺幾個？一共能擺幾個？這個長方形的面積是多少？
　　2.用表象思考、想象即圖像把握。指導學生再現前階段形成的表象，在腦中想象：用面積是1平方厘米的正方形擺以下長方形，看看各能擺幾個？它們的面積各是多少？
　　3.歸納概括即符號把握。在分組討論“長方形所含的平方厘米數與長和寬所含厘米數有什么關系”的基礎上，讓學生自己發現，歸納出長方形的面積公式。