基于相似性保持和特征變換的高維數據聚類改進算法

王家耀,謝明霞,2,郭建忠,陳 科

1.信息工程大學測繪學院,河南鄭州450052;2.75719部隊,湖北武漢430074

基于相似性保持和特征變換的高維數據聚類改進算法

王家耀1,謝明霞1,2,郭建忠1,陳 科1

1.信息工程大學測繪學院,河南鄭州450052;2.75719部隊,湖北武漢430074

提出一種基于相似性保持和特征變換的高維數據聚類改進算法。首先,通過相似性度量函數計算得到高維空間對象相似度矩陣,并利用近鄰法、Floyd最短路徑算法將相似度矩陣轉換為最短路徑距離矩陣;然后,將高維特征變換轉化為遺傳優化問題,利用特征變換降維后的二維數據進行k-均值聚類,并根據(高維坐標,降維后二維坐標)值進行RBF神經網絡訓練,當新對象輸入時,利用訓練好的神經網絡對其進行二維映射,通過判斷該對象與各聚類簇中心距離的遠近獲得其歸屬;最后,通過試驗驗證了改進相似性度量函數能夠有效表達高維數據對象間的相似性,且基于特征變換的降維方法具有可操作性。

特征變換;高維數據聚類;相似度;降維

1 引 言

聚類分析是數據挖掘研究的一個重要方向。所有的聚類問題都是在對給定數據集進行劃分的同時,根據同一簇中的對象盡可能相似、不同簇間的對象盡可能相異這一準則,設計優化函數,通過對所設計的優化問題的求解實現數據對象的聚類[1]。由于“維度困擾”的存在,目前絕大多數聚類算法在高維空間中無法得到理想的效果。為使現有聚類算法能夠適用于高維空間,可以從兩個方面進行改進:相似性度量和高維空間降維。

在高維數據相似性度量方面,就是否能獲得高維數據聚類的成效而言,指定適當的相似性(相異性)度量比選擇聚類算法更為重要。現有的高維數據相似性度量的改進方法可以概括為兩種:一是基于傳統距離度量的改進方法[2-4];二是相似性度量方法重構[5-7]。傳統的相似性度量有距離度量和相似系數。文獻[7-8]對Lk-范數和數據維數關系的研究結果說明在高維空間中用Lk-范數作距離函數時,隨著維數的增加,點與點之間距離的對比性不復存在,基于傳統Lk-范數的改進相似性度量方法本質上無法避免“維災”的影響; Cosine度量和Pearson相關系數適于高維空間中數值型數據的相似性度量,而不能用于分類型數據相似度的計算;Jaccard系數可以較好地反映高維數據在屬性上的相似程度,但不能反映其在高維空間距離上的相似程度。文獻[7-8]重新設計高維空間中的相似性度量,文獻[5]對其設計的相似性度量方法進行改進,提出度量函數 Hsim,該函數避免原低維空間中定義的距離函數在高維空間中的不適用問題,但不能用于對分類屬性數據的相似性度量。文獻[6]對函數 Hsim進行擴展使其能夠對分類型數據進行度量,但該方法仍存在一些不足,文章將在下一節對其進行具體的分析和說明。如何設計適于高維數據對象間的相似性度量方法是提高高維數據聚類算法有效性的關鍵問題。

在高維空間降維方面,降維的方式有兩種:特征(或屬性)選擇和特征(或屬性)變換。特征(或屬性)選擇在降維中存在的最大弊端在于計算的復雜度,當數據維數比較高時,子空間數目將會急劇增長,導致對子空間中各簇的搜索過程漫長而又復雜,從而使算法失效;特征(或屬性)變換方法包括PCA、LDA、KPCA、ISOMAP、LL E及其相應的改進方法等,如文獻[9-11]。現有特征變換方法的主要缺陷在于其只能獲得已知數據集的潛在低維結構,并不能給出高維空間中數據點到低維空間的確定性映射關系。

針對以上問題,主要對高維數據相似性度量的重構和基于特征變換的降維進行研究,將適于高維空間的相似性度量與降維過程中的距離保持方法相結合,使得在降維后的低維空間中,原數據集中各數據點之間在高維空間中的相似性得到有效保持。為確定原高維數據和降維后低維數據的映射關系,利用神經網絡獲取降維轉換器,當新的高維數據點輸入時,能夠快速有效地獲取其相應的低維坐標。

2 關鍵技術

2.1 相似性測度計算

高維數據對象間的相似性主要體現在屬性相似性和幾何相似性兩個方面。

定義1:屬性映射值

對于區間標度型、序數和比例標度型對象,屬性映射值表示各維信息是否存在,即是否有取值,若存在,則對應維的屬性映射值為1,反之為0;對于分類型對象,屬性映射值表示各維的取值,若各維取值是概念性的,如{好,中,差},將其進行數值化映射,即{好,中,差}→{1,0,-1}。

定義2:幾何相似度

幾何相似度S(X,Y)表示對象X和Y空間距離的遠近程度,S(X,Y)越大,表明 X和Y越相似,在空間上越接近;反之亦然。其表達式為

式中,xi、yi表示對象 X和 Y在第 i維上的屬性值。

定義3:屬性相似概率

屬性相似概率 P(txi,tyi)表示屬性 i上的幾何相似度在d維對象X和Y的總體相似度中所占的比例,即

式中,txi、tyi為對象X和Y在第i維上的屬性映射值;φ(txi,tyi)表示對象 X和Y在第i維上的屬性映射值是否相同,若 txi≠tyi,則φ(txi,tyi)=0,若txi=tyi,則φ(txi,tyi)=1。

文獻[5]所設計的高維數據相似性度量函數Hsim解決原有低維空間中定義的距離函數不適用于高維空間的問題,Hsim在高維空間中的有效性在文獻中已進行論證,其具體設計如下

式中,d為兩個對象X和Y中不全為空的維數,函數值范圍為[0,1]。該函數在設計過程中未考慮屬性之間的相似性,故不能用于分類型數據的相似性度量。為使其能夠處理分類型數據,文獻[6]對其進行擴展,具體擴展函數為

式中,若 xi=yi,則δ(xi,yi)=0;若 xi≠yi,則δ(xi,yi)=1。本文利用表1所列分類型數據來說明式(4)的不足。

表1 分類型數據Tab 1.Categorical data

根據公式(4)計算點 X和Y之間的相似性,其結果為 Hsimc(X,Y)=1/2,顯然 Hsimc所反映出的相似性與實際情況是不相符的。本文融合高維數據的屬性相似性和幾何相似性,并將不同類型數據的相似性度量函數整合到統一的 HDsim函數中,具體定義如下

針對數值型數據,本文提出的相似性度量方法首先對數據集進行標準化處理,避免維間數值大小相差較大給相似性度量帶來的不合理影響,并使其具有不依賴于幅值的特性;然后獲取數據集相應的二元特征集,即對無取值的屬性設置為0,對有取值的屬性設置為1;最后根據式(5)計算對象間的相似度。在計算過程中,化簡后的HDsim與原 Hsim相同。因此,本文設計的相似性度量函數 HDsim在處理數值型數據時能夠充分利用Hsim函數的優越性;針對二元數據,函數Hsim與 HDsim計算得到的相似度量與Jaccard系數一致;針對分類型數據(分類型數據是二元數據的推廣,它可以取多個狀態值,即多元數據),函數 HDsim計算得到的相似度量與常用的分類型數據相似性度量方法(匹配率)一致,而 Hsim已無法求得對象間的相似性。

2.2 基于相似性保持的高維空間結構流形正確展開的降維方法

為了提高高維數據聚類的效率,本文采用特征變換的方式對原高維空間進行降維,并在降維后的低維空間中保持數據對象在高維空間的近鄰關系。

根據公式

將相似度矩陣轉化為距離矩陣 HD。聚類過程中數據對象間的相似關系需要滿足兩個一致性假設:局部一致性——鄰近的數據點具有較高的相似度;全局一致性——同一流形上的數據點具有較高的相似度[12]。對于圖l所示的情況,按照HDsim進行相似度度量時,數據點1和3的相似程度明顯高于數據點1和2之間的相似度,因此不能反映圖1所示數據的全局一致性。

圖1 HDsim相似性度量的全局不一致Fig.1 Global inconsistency of similarity measureHDsim

為了解決上述問題,利用對象間的最短路徑代替不能表達流形結構的歐氏距離,通過給定鄰域大小,用近鄰法創建與距離矩陣 HD相應的鄰域圖[13-15],并判斷圖的連通性,對連通圖采用最短路徑算法,得到 HDsim相似性度量基礎上的最短路徑距離矩陣D。對每一高維數據對象隨機地賦一初始二維坐標值,通過使二維數據對象間歐氏距離趨近于高維空間對象間的最短路徑距離,對二維坐標值進行迭代優化。該過程可以近似轉化為使二維空間中各對象歐氏距離與對應原高維空間對象間最短路徑距離測度之間的誤差總和達到最小,使以下誤差函數達到最小值

式中,d′ij表示降維后二維對象間的歐氏距離。利用遺傳算法對此優化問題進行求解,誤差函數值越小,則遺傳過程中個體的適應度值越高[16]。定義個體的適應度函數為

2.3 降維轉換器的生成及聚類簇更新

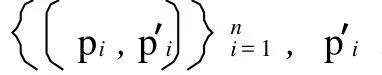
常用的基于特征變換的降維方法對原始數據進行降維后,當有新對象輸入時,不僅要對新數據對象進行處理,而且需要對整個數據集進行重新降維,其結果是嚴重影響降維聚類算法的時效性。針對該問題,利用遺傳降維所獲得的數據值對二維映射后數據對象,進行RBF(徑向基)神經網絡訓練,保存訓練好的神經網絡,從而獲得對象高維坐標到低維坐標的轉換器。當一新數據對象 pnew輸入時,利用訓練好的神經網絡對其進行低維轉換,獲得相應的低維坐標值 p降維,并根據 p降維與原聚類簇中心的距離判斷新數據對象的歸屬,即判斷完新對象的歸屬后,重新計算各聚類均值,更新各聚類簇中心。由于新對象的低維坐標是通過原降維轉換器獲取,其精度無法判斷,且降維轉換器需要通過對外來數據值對(本身并不通過該降維轉換器求取的數據值對)的學習進行更新,因此,本文在獲取新對象的低維坐標后,不利用此數據值對更新降維轉換器。

2.4 基于相似性保持和特征變換的高維數據聚類改進算法

本文提出的高維數據聚類改進算法,在降維過程中保持相似性度量在高維空間中的有效性,使數據對象在降維后的低維空間中能夠正確展開高維數據對象間的相似性結構流形。算法的流程圖如圖2所示。

圖2 基于相似性保持和特征變換的高維數據聚類改進算法流程圖Fig.2 The flow of improved high dimensional data clustering algorithm based on similarity preserving and feature transformation

3 試驗及有效性分析

3.1 仿真數據試驗

利用MA TLAB分別隨機生成7個包含50條10維、20維、50維、100維、200維、300維以及400維記錄的數據集和5個包含10條、20條、30條、50條和100條50維記錄的數據集。對仿真數據集進行遺傳降維,圖3和圖4分別為遺傳降維所用時間隨數據維數和數據量變化的對比圖。從圖中可以看出,本文提出的遺傳降維方法所用的時間與數據集的維數無關,而與數據集的數據量相關,當數據量增加時,降維所用的時間顯著增加。因此,在實際降維過程中,當數據集的數據量非常大時,為提高遺傳算法降維的效率,考慮在原始高維空間中隨機抽取若干高維數據對象進行交叉變異,獲得其相應的降維后坐標,根據所抽取對象的值對(原高維空間坐標值,降維后二維空間坐標值)進行神經網絡映射,獲得降維轉換器,并利用轉換器計算原始高維空間中未被抽取的數據對象的低維映射坐標值。

圖3 遺傳降維所用時間隨維數變化曲線Fig.3 Change curve of consuming time with dimension

圖4 遺傳降維所用時間隨數據量變化曲線Fig.4 Change curve of consuming time with data quantity

3.2 機器學習數據試驗

為驗證改進相似性保持和特征變換的高維數據聚類改進算法針對真實數據的有效性,以UCI提供的機器學習數據庫中iris(數值型)和zoo(分類型)數據集為例,分別利用k-均值、基于 PCA降維的k-均值(PCA k-means)、基于歐氏距離保持的k-均值(Euclid k-means)以及本文提出的高維數據聚類算法(HDsim k-means)對其進行聚類對比分析。為提高遺傳降維算法的效率,隨機抽取數據集中的部分數據進行降維,生成降維轉換器后對未被抽取的數據進行降維映射,獲取相應的低維坐標。在聚類分析前,去掉iris和zoo數據集中的類標識屬性,聚類后,利用聚類結果和類標識屬性信息進行對比,即對各方法獲得的聚類結果采用基于已知類標識分布的聚類質量度量方法——聚類簇純凈度PCC及聚類熵EIC進行質量評價,其定義參見文獻[17]。

圖5(a)、(b)、(c)分別為利用PCA k-means、Euclid k-means以及HDsim k-means對iris數據集的聚類可視化結果,表2和表3分別為各聚類方法所用時間和精度的對比。圖6為zoo數據集的降維聚類可視化結果,表4和表5分別為利用二步聚類、Euclid k-means以及 HDsim k-means對zoo數據集的聚類所用時間和精度的對比。為便于可視化結果的對比,各方法降維結果均已進行歸一化。針對zoo數據集,由于PCA方法僅適用于變量之間存在一定相關性的數值型數據集的降維,而不能用于處理非線性數據和分類型數據,因此,無法利用PCA k-means方法對zoo數據集進行降維聚類(降維結果無意義)。

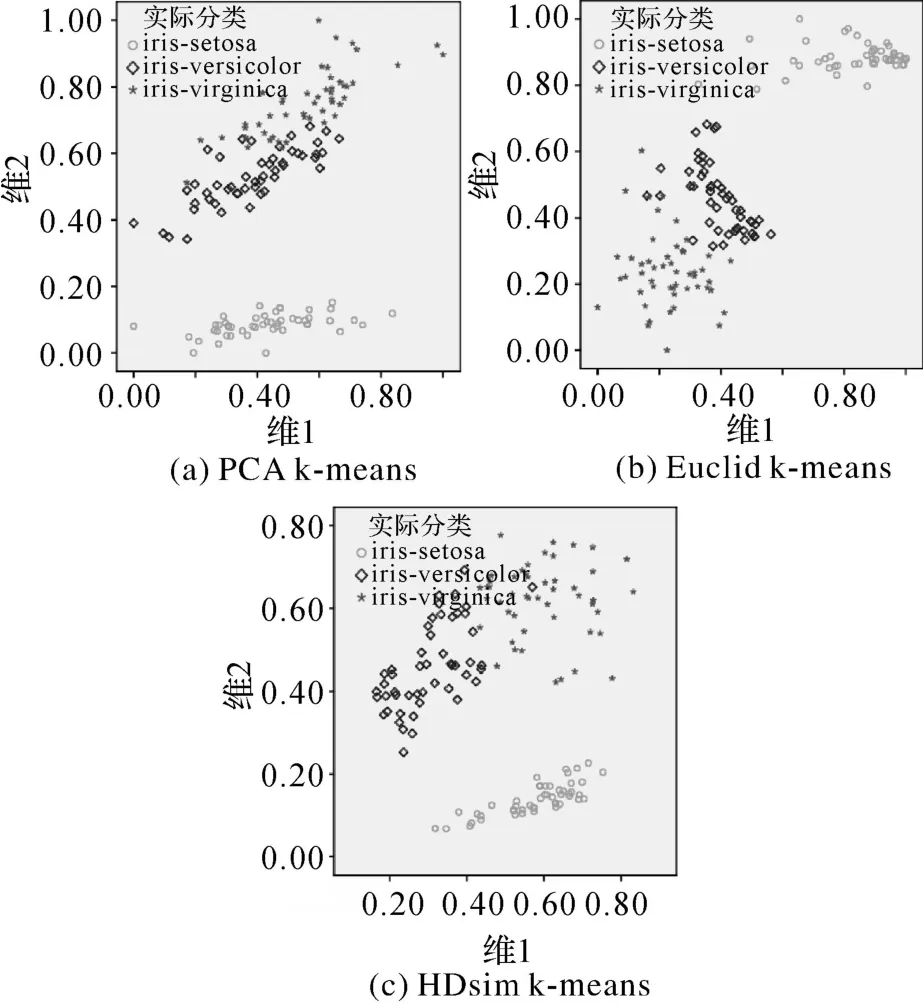
圖5 iris數據集降維聚類可視化Fig.5 Dimensionality reduction clustering visualization of data set iris

圖6 zoo數據集降維聚類可視化Fig.6 Dimensionality reduction clustering visualization of zoo set iris

表2 iris數據集各算法聚類時間對比Tab.2 Consuming time of each clustering algorithm to data set iris s

表3 iris數據集聚類結果對比Tab.3 Clustering results of data set iris

表4 zoo數據集各算法聚類時間對比Tab.4 Consuming time of each clustering algorithm to data set zoo

表5 zoo數據集聚類結果對比Tab.5 Clustering results of data set

3.3 試驗分析

k-均值聚類的精度取決于聚類個數和初始中心確定的好壞,在處理高維數據時,由于不易確定其聚類個數和初始聚類簇中心,導致聚類結果和聚類時間無法確定,而降維可視化對k-均值聚類中聚類個數和初始中心的選取具有指導意義。在確定聚類數和初始聚類簇中心后,由于k-均值聚類是對原始高維數據進行處理,而 PCA kmeans、Euclid k-means以及 HDsim k-means是對降維后的數據進行處理,降維后的數據量明顯少于原數據量,因此,僅就聚類時間(不包括數據預處理、聚類數和初始簇中心的確定所需時間)而言,PCA k-means、Euclid k-means以及 HDsim k-means的聚類時間要少于k-均值聚類。Euclid k-means和 HDsim k-means算法數據預處理階段所需時間較長,而PCA k-means所用的時間要遠遠少于 Euclid k-means和 HDsim k-means算法,但PCA應用范圍有限,主要表現在以下幾個方面:①當隨機生成的數據集維數達到170維左右時,傳統的 PCA方法已無法對其進行降維;②PCA不能對數值型以外的數據進行降維;③PCA不能處理非線性數據。

文中涉及的各降維聚類方法中高維數據對象的降維坐標是通過不同性質的降維方法(PCA、基于Euclid距離保持的降維以及基于HDsim相似性保持的降維方法)獲取的,因此,利用各方法求取的數據對象降維后的坐標之間并沒有相關性,從而導致聚類可視化結果圖5、6中各方法降維聚類結果在數據分布上不存在相似性。由可視化結果圖5可知,算法 PCA k-means、Euclid kmeans和 HDsim k-means都較好地保留iris各聚類數據的內部局部結構,但PCA k-means所獲得的聚類結果中Virginica和Versicolor兩類之間無明顯界線;由圖6可以看出,算法 Euclid kmeans和 HDsim k-means較好地保留各聚類數據的內部局部結構,但 Euclid k-means的聚類可視化中類與類界限不清晰。

從iris和zoo數據集的聚類精度對比結果可以看出,本文提出的基于相似性保持和特征變換的高維數據聚類改進算法 HDsim k-means在聚類精度上要優于傳統的經典聚類方法、PCA kmeans和 Euclid k-means。針對數值型數據集(iris),文中所提出的聚類方法的聚類純凈度及聚類熵遠遠好于 k-均值和 PCA k-means,略好于Euclid k-means;針對分類型數據(zoo),文中方法的聚類熵與二步聚類結果類似,但優于Euclid kmeans,且聚類純度最高。改進算法不僅在聚類精度上優于其他算法,而且該方法只需獲得對象間的相似度,利用遺傳交叉變異可以方便地對數據進行相似性保持的數值化降維,后續的聚類過程可以采用統一的經典聚類算法(如k-均值)完成,而不需對聚類流程進行重新設計。

4 結 論

通過對本文聚類方法與傳統聚類方法、PCA k-means以及Euclid k-means聚類結果的可視化和精度對比,證明本文提出的改進聚類算法在高維空間中的有效性和可行性。研究結果表明:①本文提出的相似性度量函數在形式上比原有公式復雜,但方法的實質只是增加了對各維屬性類型的判斷,其計算量并未增加;②在降維過程中對HDsim相似性的保持比對Euclid距離進行保持更好地保留了各聚類數據的內部局部結構;③改進聚類算法雖然在降維階段所需時間較長,但通過降維結果的可視化較好地解決了傳統k-均值不易確定聚類數和初始聚類中心的問題;④在降維后的低維空間中保持高維數據對象間相似性,即將高維數據對象間的相似程度轉化為低維空間中對象間的相似程度,則對映射后的二維樣本聚類就相當于對原始的高維樣本聚類,因此,本文提出的改進聚類算法具有可行性。

[1] CECILIA M.Clustering Problems and Their Applications [R].Durham:Duke University,1997.

[2] XIE Lihong.The Research on Clustering for High Dimensional Data[D].Wuhan:Wuhan University,2002.(謝立宏.面向高維數據的聚類算法研究[D].武漢:武漢大學,2002.)

[3] LIU Jiping,WANG Hongbin,WANG Chengbo,et al.Fuzzy Nearest Neighbor Clustering of High-dimensional Data[J]. Journal of Chinese Computer Systems,2005,26(2):261-263.(劉紀平,汪宏斌,汪誠波,等.基于模糊最近鄰的高維數據聚類[J].小型微型計算機系統,2005,26(2): 261-263.)

[4] JOSHUA Z H,MICHAEL K,RONG H Q,et al.Automated Variable Weighting in k-Means Type Clustering[J].IEEE Transactions on Pattern Analysis and MachineIntelligence,2005,27(5):657-668.

[5] YANG Fengzhao,ZHU Yangyong.An Efficient Method for Similarity Search on Quantitative Transaction Data[J]. Journal of Computer Research and Development,2004,41 (2):361-368.(楊風召,朱揚勇.一種有效的量化交易數據相似性搜索方法[J].計算機研究與發展,2004,41(2): 361-368.)

[6] ZHAO Heng.Study on Some Issues of Data Clustering in Data Mining[D].Xi’an:Xidian University,2005.(趙恒.數據挖掘中聚類若干問題研究[D].西安:西安電子科技大學,2005.)

[7] AGGARWAL C C.Re-designing Distance Functions and Distance-based Applications forHigh Dimensional Data [J].ACM SIGMOD Record,2001,30(1):13-18.

[8] AGGARW AL C C.On the Effects of Dimensionality Reduction on High Dimensional Similarity Search[C]∥Proceedings of the 20th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems.New York:ACM,2001: 256-266.

[9] LIU Xiaoming,YIN Jianwei,FENG Zhilin,et al.Orthogonal Neighborhood Preserving EmbeddingBased Dimension Reduction and Classification Method[J].Journal of Image and Graphics,2009,14(7):1319-1326.(劉小明,尹建偉,馮志林,等.正交化近鄰關系保持的降維及分類算法[J].中國圖象圖形學報,2009,14(7):1319-1326.)

[10] L I Yang.Distance-preserving Projection ofHighdimensional Data for Nonlinear Dimensionality Reduction [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(9):1243-1246.

[11] LIU Zhonghua,ZHOU Jingbo,CHEN Yi,et al.Non-linear Dimensionality Reduction Techniques of Distance-preserving Projection for Visualization and Classification[J].Acta Electronica Sinica,2009(8):1820-1825.(劉中華,周靜波,陳燚,等.距離保持投影非線性降維技術的可視化與分類[J].電子學報,2009(8):1820-1825.)

[12] WANG Na,DU Haifeng,WANG Sunan.Iterative Optimization Clustering Algorithm Based on Manifold Distance [J].Journal of Xi’an Jiaotong University,2009,43(5): 76-79.(王娜,杜海峰,王孫安.一種基于流形距離的迭代優化聚類算法[J].西安交通大學學報,2009,43(5): 76-79.)

[13] TENENBAUM J B,SILVA V,UNGFORD J C.A Global Geometric Framework for NonlinearDimensionality Reduction[J].Science,2000,290(12):2319-2323.

[14] GENG Xiepeng,DU Xiaochu,HU Peng.Spatial Clustering Method Based on Raster Distance Transform for Extended Objects[J].Acta Geodaetica et Cartographica Sinica, 2009,38(2):162-167,174.(耿協鵬,杜曉初,胡鵬.基于柵格距離變換的擴展對象空間聚類方法[J].測繪學報, 2009,38(2):162-167,174.)

[15] GUO Qingsheng,Zheng Chunyan,HU Huake.Hierarchical Clustering Method ofGroup of Points Based on the Neighborhood Graph[J].Acta Geodaetica et Cartographica Sinica,2008,37(2):256-261.(郭慶勝,鄭春燕,胡華科.基于近鄰圖的點群層次聚類方法的研究[J].測繪學報, 2008,37(2):256-261.)

[16] WANG Baowen,YAN Junmei,LIU Wenyuan,et al.High Dimensional Datas Fuzzy Clustering Based on Genetic Algorithm[J].Computer Engineering and Application, 2007,43(16):191-192,221.(王寶文,閻俊梅,劉文遠,等.基于遺傳算法的高維數據模糊聚類[J].計算機工程與應用,2007,43(16):191-192,221.)

[17] ZHANG Weijiao,LIU Chunhuang,LI Fangyu.Method of Quality Evaluation for Clustering [J].Computer Engineering,2005,31(20):10-12.(張惟皎,劉春煌,李芳玉.聚類質量的評價方法[J].計算機工程,2005,31(20): 10-12.)

Improved High Dimensional Data Clustering Algorithm Based on Similarity Preserving and Feature Transformation

WANGJiayao1,XIE Mingxia1,2,GUO Jianzhong1,CHEN Ke1
1.Institute of Surveying and Mapping,Information Engineering University,Zhengzhou 450052,China;2.75719 Troup,Wuhan 430074,China

Improved high dimensional data clustering algorithm based on similarity preserving and feature transformation is proposed.Firstly,gain the similarity matrix of high dimensional data with the designed similarity measure function,and translate it into distance matrix of the shortest path through the nearest neighbor searching method and the algorithm Floyd.Then,translate high dimensional feature transformation into the optimization and resolve this optimization problem with genetic algorithm.The reduced data is used for clustering analysis via k-means and the value pairs between the coordinates of high dimensional data and their reduced 2D coordinates are used for RBF neural network training.Determine the belongingness of new object based on the distance from the new object to each current clustering center through the trained neural network.Finally,the experimental results prove the validity of the improved similarity measure and the operability of the dimensionality reduction method based on feature transformation.

feature transformation;high dimensional data clustering;similarity measure;dimensionality reduction

WANGJiayao(1936—),male,professor, academician ofChineseAcademicofEngineering, majors in teaching and scientific research of cartography and geographic information engineering.

1001-1595(2011)03-0269-07

TP181

A

國家863計劃(2009AA12Z228);國家科技支撐計劃課題(2007BAH16B03)

(責任編輯:宋啟凡)

2010-03-10

2010-09-27

王家耀(1936—),男,教授,中國工程院院士,從事地圖制圖學與地理信息工程學科的教學與科研。

E-mail:wangjy@cae.cn